23: Breadth-First Search (BFS)

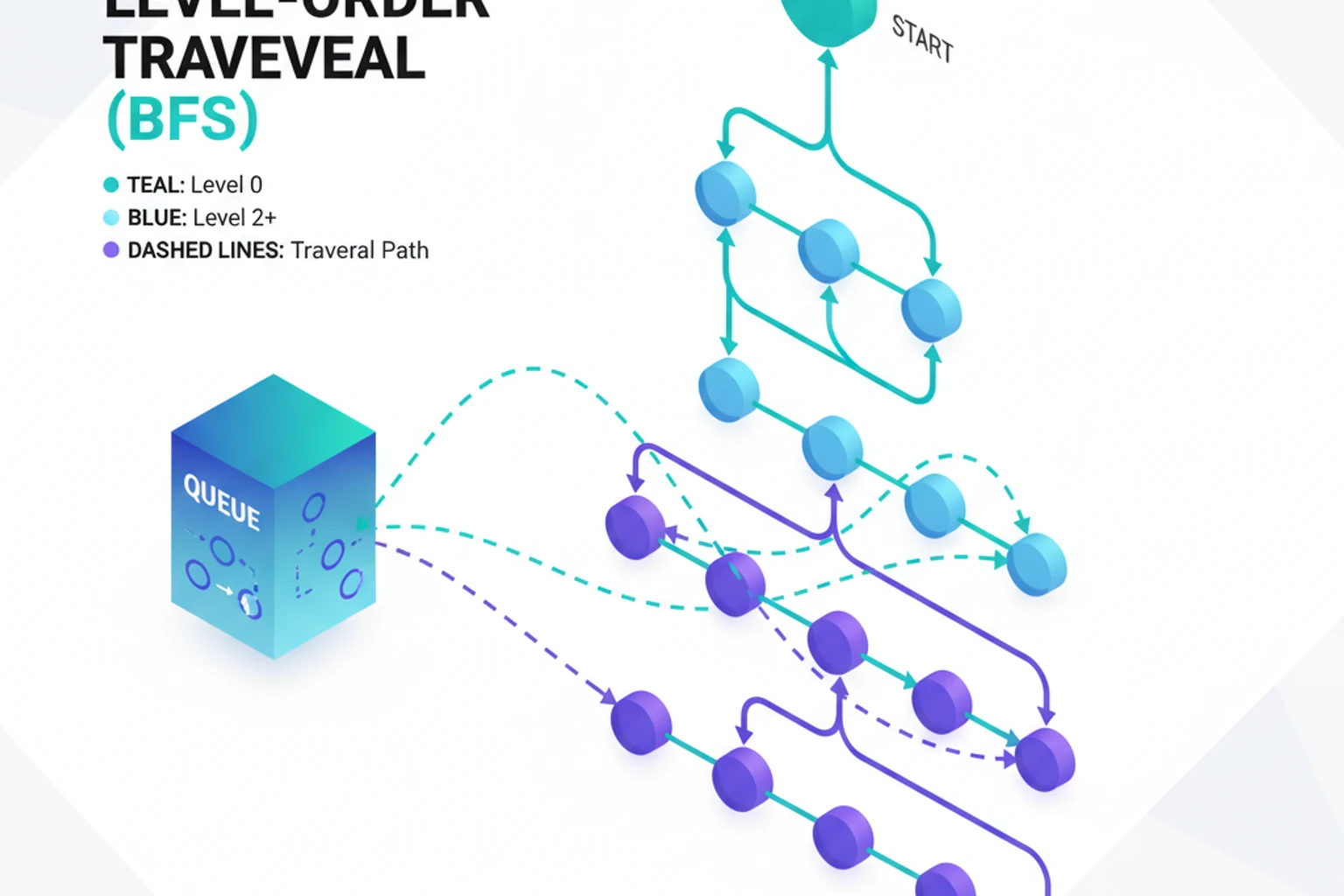
23: Breadth-First Search (BFS) Intermediate

Overview

Breadth-First Search explores a graph level by level, visiting all neighbors of a vertex before moving to the next level—like ripples spreading out from a stone dropped in water. It’s optimal for finding shortest paths in unweighted graphs and forms the foundation for many important algorithms in networking, social media, and AI.

Unlike Depth-First Search which explores deeply before backtracking, BFS systematically explores all vertices at the current level before moving to the next level. This level-by-level approach guarantees that when BFS finds a path, it’s the shortest possible path in an unweighted graph. The algorithm uses a queue data structure to maintain the order of exploration, ensuring that vertices are processed in the exact order they’re discovered.

In this chapter, you’ll master BFS implementation using queues, learn how to find shortest paths, detect connected components and bipartite graphs, and apply BFS to solve real-world problems like social network analysis and grid-based pathfinding. You’ll build practical applications including a social graph service, a grid pathfinding system, and a word ladder solver, gaining deep insight into one of computer science’s most practical graph algorithms.

By the end of this chapter, you’ll understand when BFS is the right choice over depth-first search, how to optimize it for different graph structures, and how it forms the basis for advanced algorithms like Dijkstra’s shortest path algorithm for weighted graphs.

Prerequisites

Before starting this chapter, you should have:

Complete understanding of graph representations (Chapter 21)
Strong knowledge of queues (Chapter 17)
Familiarity with DFS (Chapter 22) for comparison
Understanding of visited/distance tracking patterns

Estimated Time: ~50 minutes

What You’ll Build

By the end of this chapter, you will have created:

A complete BFS implementation with level tracking
Shortest path finder for unweighted graphs
Bipartite graph detector using BFS coloring
Grid-based pathfinding system
Social network analysis tools using BFS
Multi-source BFS for finding nearest sources

Objectives

Master breadth-first search for level-order graph traversal
Find shortest paths in unweighted graphs with BFS
Detect connected components and bipartite graphs
Implement BFS using queues for efficient exploration
Apply BFS to solve real-world problems like social network analysis

How BFS Works

BFS explores a graph by:

Starting at a source vertex
Visiting all immediate neighbors (level 1)
Visiting all neighbors of those neighbors (level 2)
Continuing level by level until all reachable vertices are visited

Graph:        0---1---2
              |   |
              3---4

BFS from 0: Level 0: [0]
            Level 1: [1, 3]
            Level 2: [2, 4]

Order: [0, 1, 3, 2, 4]

BFS Visual Step-by-Step Trace

Understanding BFS execution through detailed visualization:

<?php

declare(strict_types=1);

class BFSVisualizer
{
    private array $graph;

    public function __construct(array $graph)
    {
        $this->graph = $graph;
    }

    // Visualize BFS execution step by step
    public function visualizeBFS(int $start): void
    {
        echo "=== BFS Traversal Visualization ===\n\n";
        echo "Graph Structure:\n";
        $this->printGraph();
        echo "\n";

        echo "Starting BFS from vertex $start\n";
        echo str_repeat('=', 60) . "\n\n";

        $visited = [$start => true];
        $queue = [$start];
        $level = 0;
        $stepCount = 0;

        while (!empty($queue)) {
            $levelSize = count($queue);
            echo "Level $level:\n";

            for ($i = 0; $i < $levelSize; $i++) {
                $vertex = array_shift($queue);
                $stepCount++;

                echo "  Step $stepCount: Process vertex $vertex\n";
                echo "    Current queue: [" . implode(', ', $queue) . "]\n";
                echo "    Visited: {" . implode(', ', array_keys($visited)) . "}\n";

                $neighbors = $this->graph[$vertex] ?? [];
                $newNeighbors = [];

                foreach ($neighbors as $neighbor) {
                    if (!isset($visited[$neighbor])) {
                        $visited[$neighbor] = true;
                        $queue[] = $neighbor;
                        $newNeighbors[] = $neighbor;
                    }
                }

                if (!empty($newNeighbors)) {
                    echo "    Added to queue: [" . implode(', ', $newNeighbors) . "]\n";
                } else {
                    echo "    No new neighbors to add\n";
                }

                echo "    Queue after: [" . implode(', ', $queue) . "]\n";
                echo "\n";
            }

            $level++;
        }

        echo "=== Summary ===\n";
        echo "Total vertices visited: " . count($visited) . "\n";
        echo "Maximum level reached: " . ($level - 1) . "\n";
    }

    private function printGraph(): void
    {
        foreach ($this->graph as $vertex => $neighbors) {
            echo "  $vertex: [" . implode(', ', $neighbors) . "]\n";
        }
    }

    // Visualize level-by-level exploration
    public function visualizeLevels(int $start): void
    {
        echo "\n=== BFS Level Visualization ===\n\n";

        echo "Starting from vertex $start:\n\n";

        $visited = [$start => true];
        $currentLevel = [$start];
        $level = 0;

        while (!empty($currentLevel)) {
            echo "Level $level: ";
            $this->drawLevel($currentLevel);
            echo "\n";

            $nextLevel = [];
            foreach ($currentLevel as $vertex) {
                foreach ($this->graph[$vertex] ?? [] as $neighbor) {
                    if (!isset($visited[$neighbor])) {
                        $visited[$neighbor] = true;
                        $nextLevel[] = $neighbor;
                    }
                }
            }

            $currentLevel = $nextLevel;
            $level++;
        }

        echo "\nLike ripples in water, BFS expands outward level by level\n";
    }

    private function drawLevel(array $vertices): void
    {
        $visual = implode('---', array_map(fn($v) => "[$v]", $vertices));
        echo $visual;
    }
}

// Example: Visualize BFS on a simple graph
$graph = [
    0 => [1, 3],
    1 => [0, 2, 4],
    2 => [1],
    3 => [0, 4],
    4 => [1, 3]
];

$visualizer = new BFSVisualizer($graph);
$visualizer->visualizeBFS(0);
$visualizer->visualizeLevels(0);

/*
Output:
=== BFS Traversal Visualization ===

Graph Structure:
  0: [1, 3]
  1: [0, 2, 4]
  2: [1]
  3: [0, 4]
  4: [1, 3]

Starting BFS from vertex 0
============================================================

Level 0:
  Step 1: Process vertex 0
    Current queue: []
    Visited: {0}
    Added to queue: [1, 3]
    Queue after: [1, 3]

Level 1:
  Step 2: Process vertex 1
    Current queue: [3]
    Visited: {0, 1}
    Added to queue: [2, 4]
    Queue after: [3, 2, 4]

  Step 3: Process vertex 3
    Current queue: [2, 4]
    Visited: {0, 1, 3}
    No new neighbors to add (0 already visited, 4 already in queue)
    Queue after: [2, 4]

Level 2:
  Step 4: Process vertex 2
    Current queue: [4]
    Visited: {0, 1, 3, 2}
    No new neighbors to add
    Queue after: [4]

  Step 5: Process vertex 4
    Current queue: []
    Visited: {0, 1, 3, 2, 4}
    No new neighbors to add
    Queue after: []

=== Summary ===
Total vertices visited: 5
Maximum level reached: 2

=== BFS Level Visualization ===

Starting from vertex 0:

Level 0: [0]
Level 1: [1]---[3]
Level 2: [2]---[4]

Like ripples in water, BFS expands outward level by level
*/

BFS Queue State Visualization

Understanding how the queue changes during BFS:

<?php

declare(strict_types=1);

class BFSQueueVisualizer
{
    // Visualize queue operations in detail
    public function visualizeQueue(array $graph, int $start): void
    {
        echo "=== BFS Queue Operations ===\n\n";

        $visited = [$start => true];
        $queue = [$start];
        $step = 0;

        $this->printQueueState($step++, $queue, "INIT", $start, "Start vertex");

        while (!empty($queue)) {
            $vertex = array_shift($queue);
            $this->printQueueState($step++, $queue, "DEQUEUE", $vertex, "Processing");

            foreach ($graph[$vertex] ?? [] as $neighbor) {
                if (!isset($visited[$neighbor])) {
                    $visited[$neighbor] = true;
                    $queue[] = $neighbor;
                    $this->printQueueState($step++, $queue, "ENQUEUE", $neighbor,
                                         "From vertex $vertex");
                }
            }
        }

        echo "\nQueue Operations Summary:\n";
        echo "- Queue follows FIFO (First-In-First-Out) principle\n";
        echo "- Enqueue: Add to back of queue (array_push)\n";
        echo "- Dequeue: Remove from front of queue (array_shift)\n";
        echo "- This ensures level-by-level exploration\n";
    }

    private function printQueueState(int $step, array $queue, string $op, int $vertex, string $note): void
    {
        echo "Step $step: $op vertex $vertex ($note)\n";
        echo "  Queue: [";

        if (empty($queue)) {
            echo "empty";
        } else {
            foreach ($queue as $i => $v) {
                echo $i === 0 ? "← $v" : " $v";
                if ($i === count($queue) - 1 && count($queue) > 1) {
                    echo " ←";
                }
            }
        }

        echo "]\n";
        echo "         " . ($op === 'DEQUEUE' ? "^front" : str_repeat(' ', count($queue) * 3) . "back^") . "\n\n";
    }
}

$graph = [
    0 => [1, 2],
    1 => [0, 3],
    2 => [0, 4],
    3 => [1],
    4 => [2]
];

$queueViz = new BFSQueueVisualizer();
$queueViz->visualizeQueue($graph, 0);

/*
Output shows FIFO queue behavior:

=== BFS Queue Operations ===

Step 0: INIT vertex 0 (Start vertex)
  Queue: [← 0 ←]
            back^

Step 1: DEQUEUE vertex 0 (Processing)
  Queue: [empty]
         ^front

Step 2: ENQUEUE vertex 1 (From vertex 0)
  Queue: [← 1 ←]
            back^

Step 3: ENQUEUE vertex 2 (From vertex 0)
  Queue: [← 1 2 ←]
               back^

Step 4: DEQUEUE vertex 1 (Processing)
  Queue: [← 2]
         ^front

Step 5: ENQUEUE vertex 3 (From vertex 1)
  Queue: [← 2 3 ←]
               back^

... and so on ...
*/

Basic BFS Implementation

<?php

declare(strict_types=1);

class BFS
{
    // BFS traversal
    public function traverse(array $graph, int $start): array
    {
        $visited = [$start => true];
        $result = [$start];
        $queue = [$start];

        while (!empty($queue)) {
            $vertex = array_shift($queue);

            foreach ($graph[$vertex] ?? [] as $neighbor) {
                if (!isset($visited[$neighbor])) {
                    $visited[$neighbor] = true;
                    $result[] = $neighbor;
                    $queue[] = $neighbor;
                }
            }
        }

        return $result;
    }

    // BFS with level tracking
    public function traverseByLevel(array $graph, int $start): array
    {
        $visited = [$start => true];
        $levels = [[$start]];
        $queue = [[$start, 0]];  // [vertex, level]

        while (!empty($queue)) {
            [$vertex, $level] = array_shift($queue);

            foreach ($graph[$vertex] ?? [] as $neighbor) {
                if (!isset($visited[$neighbor])) {
                    $visited[$neighbor] = true;

                    if (!isset($levels[$level + 1])) {
                        $levels[$level + 1] = [];
                    }
                    $levels[$level + 1][] = $neighbor;

                    $queue[] = [$neighbor, $level + 1];
                }
            }
        }

        return $levels;
    }

    // BFS for all components (disconnected graphs)
    public function traverseAll(array $graph): array
    {
        $visited = [];
        $components = [];

        foreach (array_keys($graph) as $vertex) {
            if (!isset($visited[$vertex])) {
                $component = $this->bfsComponent($graph, $vertex, $visited);
                $components[] = $component;
            }
        }

        return $components;
    }

    private function bfsComponent(array $graph, int $start, array &$visited): array
    {
        $component = [$start];
        $visited[$start] = true;
        $queue = [$start];

        while (!empty($queue)) {
            $vertex = array_shift($queue);

            foreach ($graph[$vertex] ?? [] as $neighbor) {
                if (!isset($visited[$neighbor])) {
                    $visited[$neighbor] = true;
                    $component[] = $neighbor;
                    $queue[] = $neighbor;
                }
            }
        }

        return $component;
    }
}

// Example usage
$graph = [
    0 => [1, 3],
    1 => [0, 2, 4],
    2 => [1],
    3 => [0, 4],
    4 => [1, 3]
];

$bfs = new BFS();
print_r($bfs->traverse($graph, 0));  // [0, 1, 3, 2, 4]

print_r($bfs->traverseByLevel($graph, 0));
// [[0], [1, 3], [2, 4]]

// Disconnected graph
$disconnected = [
    0 => [1],
    1 => [0],
    2 => [3],
    3 => [2]
];

print_r($bfs->traverseAll($disconnected));  // [[0, 1], [2, 3]]

Shortest Path in Unweighted Graph

BFS finds the shortest path in graphs where all edges have equal weight.

<?php

declare(strict_types=1);

class BFSShortestPath
{
    // Find shortest path from start to end
    public function findPath(array $graph, int $start, int $end): ?array
    {
        if ($start === $end) {
            return [$start];
        }

        $visited = [$start => true];
        $parent = [$start => null];
        $queue = [$start];

        while (!empty($queue)) {
            $vertex = array_shift($queue);

            foreach ($graph[$vertex] ?? [] as $neighbor) {
                if (!isset($visited[$neighbor])) {
                    $visited[$neighbor] = true;
                    $parent[$neighbor] = $vertex;
                    $queue[] = $neighbor;

                    // Found the destination
                    if ($neighbor === $end) {
                        return $this->reconstructPath($parent, $start, $end);
                    }
                }
            }
        }

        return null;  // No path found
    }

    private function reconstructPath(array $parent, int $start, int $end): array
    {
        $path = [];
        $current = $end;

        while ($current !== null) {
            array_unshift($path, $current);
            $current = $parent[$current];
        }

        return $path;
    }

    // Find shortest distance from start to all vertices
    public function findAllDistances(array $graph, int $start): array
    {
        $distances = [$start => 0];
        $queue = [$start];

        while (!empty($queue)) {
            $vertex = array_shift($queue);
            $currentDistance = $distances[$vertex];

            foreach ($graph[$vertex] ?? [] as $neighbor) {
                if (!isset($distances[$neighbor])) {
                    $distances[$neighbor] = $currentDistance + 1;
                    $queue[] = $neighbor;
                }
            }
        }

        return $distances;
    }

    // Find shortest path distance
    public function findDistance(array $graph, int $start, int $end): ?int
    {
        $distances = $this->findAllDistances($graph, $start);
        return $distances[$end] ?? null;
    }
}

// Example
$graph = [
    0 => [1, 2],
    1 => [0, 3],
    2 => [0, 3, 4],
    3 => [1, 2, 4],
    4 => [2, 3]
];

$pathFinder = new BFSShortestPath();
print_r($pathFinder->findPath($graph, 0, 4));  // [0, 2, 4]

echo "Distance from 0 to 4: " . $pathFinder->findDistance($graph, 0, 4) . "\n";  // 2

print_r($pathFinder->findAllDistances($graph, 0));
// [0 => 0, 1 => 1, 2 => 1, 3 => 2, 4 => 2]

Finding All Shortest Paths

Sometimes you need to find all shortest paths between two vertices, not just one. This is useful for network routing (multiple equal-cost paths), game pathfinding (multiple valid routes), or analyzing path diversity.

<?php

declare(strict_types=1);

class BFSAllShortestPaths
{
    // Find all shortest paths from start to end
    public function findAllPaths(array $graph, int $start, int $end): array
    {
        if ($start === $end) {
            return [[$start]];
        }

        $distances = [$start => 0];
        $parents = [$start => []];
        $queue = [$start];

        // First BFS: Find shortest distance and all possible parents
        while (!empty($queue)) {
            $vertex = array_shift($queue);
            $currentDistance = $distances[$vertex];

            foreach ($graph[$vertex] ?? [] as $neighbor) {
                if (!isset($distances[$neighbor])) {
                    $distances[$neighbor] = $currentDistance + 1;
                    $parents[$neighbor] = [$vertex];
                    $queue[] = $neighbor;
                } elseif ($distances[$neighbor] === $currentDistance + 1) {
                    // Same distance - add as another parent
                    $parents[$neighbor][] = $vertex;
                }
            }
        }

        // If end is unreachable
        if (!isset($distances[$end])) {
            return [];
        }

        // Second phase: Reconstruct all paths using DFS
        $allPaths = [];
        $this->reconstructAllPaths($parents, $start, $end, [$end], $allPaths);

        return $allPaths;
    }

    private function reconstructAllPaths(
        array $parents,
        int $start,
        int $current,
        array $path,
        array &$allPaths
    ): void {
        if ($current === $start) {
            $allPaths[] = array_reverse($path);
            return;
        }

        foreach ($parents[$current] ?? [] as $parent) {
            $this->reconstructAllPaths($parents, $start, $parent, [...$path, $parent], $allPaths);
        }
    }

    // Count number of shortest paths
    public function countShortestPaths(array $graph, int $start, int $end): int
    {
        $distances = [$start => 0];
        $pathCounts = [$start => 1];
        $queue = [$start];

        while (!empty($queue)) {
            $vertex = array_shift($queue);
            $currentDistance = $distances[$vertex];

            foreach ($graph[$vertex] ?? [] as $neighbor) {
                if (!isset($distances[$neighbor])) {
                    $distances[$neighbor] = $currentDistance + 1;
                    $pathCounts[$neighbor] = $pathCounts[$vertex];
                    $queue[] = $neighbor;
                } elseif ($distances[$neighbor] === $currentDistance + 1) {
                    // Same distance - add to path count
                    $pathCounts[$neighbor] += $pathCounts[$vertex];
                }
            }
        }

        return $pathCounts[$end] ?? 0;
    }
}

// Example
$graph = [
    0 => [1, 2],
    1 => [0, 3],
    2 => [0, 3, 4],
    3 => [1, 2, 4],
    4 => [2, 3]
];

$allPaths = new BFSAllShortestPaths();
$paths = $allPaths->findAllPaths($graph, 0, 4);
print_r($paths);
// [
//   [0, 2, 4],
//   [0, 1, 3, 4]
// ]

echo "Number of shortest paths: " . $allPaths->countShortestPaths($graph, 0, 4) . "\n";  // 2

Bidirectional BFS

Bidirectional BFS searches from both the start and end simultaneously, meeting in the middle. This dramatically reduces the search space from O(b^d) to O(b^(d/2)) where b is the branching factor and d is the depth, making it much faster for large graphs.

<?php

declare(strict_types=1);

class BidirectionalBFS
{
    // Find shortest path using bidirectional BFS
    public function findPath(array $graph, int $start, int $end): ?array
    {
        if ($start === $end) {
            return [$start];
        }

        // Forward search from start
        $forwardVisited = [$start => 0];  // vertex => distance
        $forwardParent = [$start => null];
        $forwardQueue = [$start];

        // Backward search from end
        $backwardVisited = [$end => 0];
        $backwardParent = [$end => null];
        $backwardQueue = [$end];

        $meetingPoint = null;

        while (!empty($forwardQueue) && !empty($backwardQueue)) {
            // Expand forward search
            $forwardSize = count($forwardQueue);
            for ($i = 0; $i < $forwardSize; $i++) {
                $vertex = array_shift($forwardQueue);
                $distance = $forwardVisited[$vertex];

                foreach ($graph[$vertex] ?? [] as $neighbor) {
                    if (!isset($forwardVisited[$neighbor])) {
                        $forwardVisited[$neighbor] = $distance + 1;
                        $forwardParent[$neighbor] = $vertex;
                        $forwardQueue[] = $neighbor;

                        // Check if backward search has visited this vertex
                        if (isset($backwardVisited[$neighbor])) {
                            $meetingPoint = $neighbor;
                            break 2;  // Break out of both loops
                        }
                    }
                }
            }

            if ($meetingPoint !== null) {
                break;
            }

            // Expand backward search
            $backwardSize = count($backwardQueue);
            for ($i = 0; $i < $backwardSize; $i++) {
                $vertex = array_shift($backwardQueue);
                $distance = $backwardVisited[$vertex];

                foreach ($graph[$vertex] ?? [] as $neighbor) {
                    if (!isset($backwardVisited[$neighbor])) {
                        $backwardVisited[$neighbor] = $distance + 1;
                        $backwardParent[$neighbor] = $vertex;
                        $backwardQueue[] = $neighbor;

                        // Check if forward search has visited this vertex
                        if (isset($forwardVisited[$neighbor])) {
                            $meetingPoint = $neighbor;
                            break 2;  // Break out of both loops
                        }
                    }
                }
            }
        }

        if ($meetingPoint === null) {
            return null;  // No path found
        }

        // Reconstruct path: start -> meeting point -> end
        $path = $this->reconstructPath($forwardParent, $start, $meetingPoint);
        $pathEnd = $this->reconstructPath($backwardParent, $end, $meetingPoint);
        array_shift($pathEnd);  // Remove meeting point duplicate
        $pathEnd = array_reverse($pathEnd);

        return array_merge($path, $pathEnd);
    }

    private function reconstructPath(array $parent, int $start, int $end): array
    {
        $path = [];
        $current = $end;

        while ($current !== null) {
            array_unshift($path, $current);
            $current = $parent[$current] ?? null;
        }

        return $path;
    }

    // Find shortest distance using bidirectional BFS
    public function findDistance(array $graph, int $start, int $end): ?int
    {
        if ($start === $end) {
            return 0;
        }

        $forwardVisited = [$start => 0];
        $backwardVisited = [$end => 0];
        $forwardQueue = [$start];
        $backwardQueue = [$end];

        while (!empty($forwardQueue) && !empty($backwardQueue)) {
            // Expand forward
            $vertex = array_shift($forwardQueue);
            $distance = $forwardVisited[$vertex];

            foreach ($graph[$vertex] ?? [] as $neighbor) {
                if (!isset($forwardVisited[$neighbor])) {
                    $forwardVisited[$neighbor] = $distance + 1;
                    $forwardQueue[] = $neighbor;

                    if (isset($backwardVisited[$neighbor])) {
                        return $forwardVisited[$neighbor] + $backwardVisited[$neighbor];
                    }
                }
            }

            // Expand backward
            $vertex = array_shift($backwardQueue);
            $distance = $backwardVisited[$vertex];

            foreach ($graph[$vertex] ?? [] as $neighbor) {
                if (!isset($backwardVisited[$neighbor])) {
                    $backwardVisited[$neighbor] = $distance + 1;
                    $backwardQueue[] = $neighbor;

                    if (isset($forwardVisited[$neighbor])) {
                        return $forwardVisited[$neighbor] + $backwardVisited[$neighbor];
                    }
                }
            }
        }

        return null;  // No path found
    }
}

// Example
$graph = [
    0 => [1, 2],
    1 => [0, 3, 4],
    2 => [0, 5],
    3 => [1, 6],
    4 => [1, 6],
    5 => [2, 6],
    6 => [3, 4, 5]
];

$bidirectional = new BidirectionalBFS();
$path = $bidirectional->findPath($graph, 0, 6);
print_r($path);  // [0, 1, 3, 6] or [0, 1, 4, 6] or [0, 2, 5, 6]

echo "Distance: " . $bidirectional->findDistance($graph, 0, 6) . "\n";  // 3

Bipartite Graph Detection

Checking if a graph can be colored with two colors such that no adjacent vertices have the same color.

<?php

declare(strict_types=1);

class BipartiteDetector
{
    private const COLOR_A = 0;
    private const COLOR_B = 1;

    // Check if graph is bipartite
    public function isBipartite(array $graph): bool
    {
        $colors = [];

        // Check all components (for disconnected graphs)
        foreach (array_keys($graph) as $vertex) {
            if (!isset($colors[$vertex])) {
                if (!$this->bfsColorCheck($graph, $vertex, $colors)) {
                    return false;
                }
            }
        }

        return true;
    }

    private function bfsColorCheck(array $graph, int $start, array &$colors): bool
    {
        $colors[$start] = self::COLOR_A;
        $queue = [$start];

        while (!empty($queue)) {
            $vertex = array_shift($queue);
            $currentColor = $colors[$vertex];
            $neighborColor = $currentColor === self::COLOR_A ? self::COLOR_B : self::COLOR_A;

            foreach ($graph[$vertex] ?? [] as $neighbor) {
                if (!isset($colors[$neighbor])) {
                    $colors[$neighbor] = $neighborColor;
                    $queue[] = $neighbor;
                } elseif ($colors[$neighbor] !== $neighborColor) {
                    // Neighbor has same color - not bipartite
                    return false;
                }
            }
        }

        return true;
    }

    // Get the two sets if bipartite
    public function getTwoSets(array $graph): ?array
    {
        $colors = [];

        foreach (array_keys($graph) as $vertex) {
            if (!isset($colors[$vertex])) {
                if (!$this->bfsColorCheck($graph, $vertex, $colors)) {
                    return null;  // Not bipartite
                }
            }
        }

        $setA = [];
        $setB = [];

        foreach ($colors as $vertex => $color) {
            if ($color === self::COLOR_A) {
                $setA[] = $vertex;
            } else {
                $setB[] = $vertex;
            }
        }

        return [$setA, $setB];
    }
}

// Example - Bipartite graph (e.g., students and courses)
$bipartite = [
    'Alice' => ['Math', 'Physics'],
    'Bob' => ['Math', 'Chemistry'],
    'Charlie' => ['Physics', 'Chemistry'],
    'Math' => ['Alice', 'Bob'],
    'Physics' => ['Alice', 'Charlie'],
    'Chemistry' => ['Bob', 'Charlie']
];

$detector = new BipartiteDetector();
echo $detector->isBipartite($bipartite) ? "Bipartite\n" : "Not bipartite\n";
// Bipartite

$sets = $detector->getTwoSets($bipartite);
echo "Set A (students): " . implode(', ', $sets[0]) . "\n";
echo "Set B (courses): " . implode(', ', $sets[1]) . "\n";

// Example - Not bipartite (contains odd cycle)
$notBipartite = [
    0 => [1, 2],
    1 => [0, 2],
    2 => [0, 1]  // Triangle - odd cycle
];

echo $detector->isBipartite($notBipartite) ? "Bipartite\n" : "Not bipartite\n";
// Not bipartite

Kahn’s Algorithm (BFS-based Topological Sort)

While DFS-based topological sort is common, Kahn’s algorithm uses BFS and is often more intuitive. It works by repeatedly removing vertices with no incoming edges (in-degree 0), maintaining a queue of such vertices. This is particularly useful when you need level-by-level processing or when dealing with dependency graphs.

<?php

declare(strict_types=1);

class KahnsTopologicalSort
{
    // Topological sort using Kahn's algorithm (BFS-based)
    public function topologicalSort(array $graph): ?array
    {
        // Calculate in-degrees for all vertices
        $inDegree = [];

        // Initialize in-degrees
        foreach (array_keys($graph) as $vertex) {
            $inDegree[$vertex] = 0;
        }

        // Count in-degrees
        foreach ($graph as $vertex => $neighbors) {
            foreach ($neighbors as $neighbor) {
                $inDegree[$neighbor] = ($inDegree[$neighbor] ?? 0) + 1;
            }
        }

        // Find all vertices with in-degree 0
        $queue = [];
        foreach ($inDegree as $vertex => $degree) {
            if ($degree === 0) {
                $queue[] = $vertex;
            }
        }

        $result = [];
        $processedCount = 0;

        // Process vertices with no incoming edges
        while (!empty($queue)) {
            $vertex = array_shift($queue);
            $result[] = $vertex;
            $processedCount++;

            // Reduce in-degree of neighbors
            foreach ($graph[$vertex] ?? [] as $neighbor) {
                $inDegree[$neighbor]--;

                // If in-degree becomes 0, add to queue
                if ($inDegree[$neighbor] === 0) {
                    $queue[] = $neighbor;
                }
            }
        }

        // Check for cycle (if not all vertices processed, there's a cycle)
        if ($processedCount !== count($graph)) {
            return null;  // Graph has cycle
        }

        return $result;
    }

    // Check if graph is a DAG (Directed Acyclic Graph)
    public function isDAG(array $graph): bool
    {
        return $this->topologicalSort($graph) !== null;
    }

    // Get topological sort levels (vertices at same level can be processed in parallel)
    public function topologicalSortLevels(array $graph): ?array
    {
        $inDegree = [];

        foreach (array_keys($graph) as $vertex) {
            $inDegree[$vertex] = 0;
        }

        foreach ($graph as $vertex => $neighbors) {
            foreach ($neighbors as $neighbor) {
                $inDegree[$neighbor] = ($inDegree[$neighbor] ?? 0) + 1;
            }
        }

        $levels = [];
        $currentLevel = [];

        // Find initial level (in-degree 0)
        foreach ($inDegree as $vertex => $degree) {
            if ($degree === 0) {
                $currentLevel[] = $vertex;
            }
        }

        $processedCount = 0;

        while (!empty($currentLevel)) {
            $levels[] = $currentLevel;
            $nextLevel = [];

            foreach ($currentLevel as $vertex) {
                $processedCount++;

                foreach ($graph[$vertex] ?? [] as $neighbor) {
                    $inDegree[$neighbor]--;

                    if ($inDegree[$neighbor] === 0) {
                        $nextLevel[] = $neighbor;
                    }
                }
            }

            $currentLevel = $nextLevel;
        }

        if ($processedCount !== count($graph)) {
            return null;  // Cycle detected
        }

        return $levels;
    }
}

// Example - Course prerequisites
$courses = [
    'CS101' => ['CS201'],           // CS101 is prerequisite for CS201
    'CS201' => ['CS301', 'CS302'],
    'MATH101' => ['CS201', 'CS202'],
    'CS301' => [],
    'CS302' => [],
    'CS202' => []
];

$kahn = new KahnsTopologicalSort();
$order = $kahn->topologicalSort($courses);
print_r($order);
// ['CS101', 'MATH101', 'CS201', 'CS202', 'CS301', 'CS302']
// or ['MATH101', 'CS101', 'CS201', 'CS301', 'CS302', 'CS202']
// (CS101 and MATH101 can be in any order)

$levels = $kahn->topologicalSortLevels($courses);
print_r($levels);
// [
//   ['CS101', 'MATH101'],  // Level 0: Can take these first
//   ['CS201'],              // Level 1: After level 0
//   ['CS202', 'CS301', 'CS302']  // Level 2: After level 1
// ]

// Example - Graph with cycle
$cyclic = [
    0 => [1],
    1 => [2],
    2 => [0]  // Cycle: 0 -> 1 -> 2 -> 0
];

$result = $kahn->topologicalSort($cyclic);
echo $result === null ? "Graph has cycle\n" : "Valid topological order\n";
// Graph has cycle

0-1 BFS

Optimized BFS for graphs with edge weights of only 0 and 1. This variant uses a deque (double-ended queue) to prioritize zero-weight edges, adding them to the front of the queue while adding one-weight edges to the back. This ensures we always process vertices with the shortest distance first, making it more efficient than standard BFS for this special case.

<?php

declare(strict_types=1);

class ZeroOneBFS
{
    // Shortest path in 0-1 weighted graph using deque
    public function shortestPath(array $graph, int $start, int $end): ?int
    {
        $distances = array_fill(0, count($graph), PHP_INT_MAX);
        $distances[$start] = 0;

        $deque = [$start];

        while (!empty($deque)) {
            $vertex = array_shift($deque);

            if ($vertex === $end) {
                return $distances[$end];
            }

            foreach ($graph[$vertex] ?? [] as $edge) {
                $neighbor = $edge['vertex'];
                $weight = $edge['weight'];
                $newDistance = $distances[$vertex] + $weight;

                if ($newDistance < $distances[$neighbor]) {
                    $distances[$neighbor] = $newDistance;

                    if ($weight === 0) {
                        // Add to front for 0-weight edges
                        array_unshift($deque, $neighbor);
                    } else {
                        // Add to back for 1-weight edges
                        $deque[] = $neighbor;
                    }
                }
            }
        }

        return $distances[$end] === PHP_INT_MAX ? null : $distances[$end];
    }
}

// Example - Grid where you can move freely or climb (cost 1)
$grid = [
    0 => [['vertex' => 1, 'weight' => 0], ['vertex' => 3, 'weight' => 1]],
    1 => [['vertex' => 0, 'weight' => 0], ['vertex' => 2, 'weight' => 0]],
    2 => [['vertex' => 1, 'weight' => 0], ['vertex' => 4, 'weight' => 1]],
    3 => [['vertex' => 0, 'weight' => 1], ['vertex' => 4, 'weight' => 0]],
    4 => [['vertex' => 2, 'weight' => 1], ['vertex' => 3, 'weight' => 0]]
];

$bfs01 = new ZeroOneBFS();
echo "Shortest distance: " . $bfs01->shortestPath($grid, 0, 4) . "\n";  // 1

Multi-Source BFS

Starting BFS from multiple source vertices simultaneously. This technique is useful when you need to find the nearest source to each vertex, such as finding the nearest hospital in a city map or the nearest server in a network. All sources are initialized with distance 0 and added to the queue, then BFS proceeds normally.

<?php

declare(strict_types=1);

class MultiSourceBFS
{
    // Find shortest distance from any source to all vertices
    public function findDistances(array $graph, array $sources): array
    {
        $distances = [];
        $queue = [];

        // Initialize all sources with distance 0
        foreach ($sources as $source) {
            $distances[$source] = 0;
            $queue[] = $source;
        }

        while (!empty($queue)) {
            $vertex = array_shift($queue);
            $currentDistance = $distances[$vertex];

            foreach ($graph[$vertex] ?? [] as $neighbor) {
                if (!isset($distances[$neighbor])) {
                    $distances[$neighbor] = $currentDistance + 1;
                    $queue[] = $neighbor;
                }
            }
        }

        return $distances;
    }

    // Find nearest source for each vertex
    public function findNearestSource(array $graph, array $sources): array
    {
        $nearest = [];
        $queue = [];

        // Initialize all sources
        foreach ($sources as $source) {
            $nearest[$source] = $source;
            $queue[] = $source;
        }

        while (!empty($queue)) {
            $vertex = array_shift($queue);
            $sourceVertex = $nearest[$vertex];

            foreach ($graph[$vertex] ?? [] as $neighbor) {
                if (!isset($nearest[$neighbor])) {
                    $nearest[$neighbor] = $sourceVertex;
                    $queue[] = $neighbor;
                }
            }
        }

        return $nearest;
    }
}

// Example - Multiple hospitals serving areas
$cityMap = [
    0 => [1, 2],
    1 => [0, 3],
    2 => [0, 3, 4],
    3 => [1, 2, 4, 5],
    4 => [2, 3, 6],
    5 => [3, 6],
    6 => [4, 5]
];

$hospitals = [0, 5];  // Hospitals at vertices 0 and 5

$multiBFS = new MultiSourceBFS();
$distances = $multiBFS->findDistances($cityMap, $hospitals);
echo "Distance to nearest hospital:\n";
print_r($distances);
// [0 => 0, 1 => 1, 2 => 1, 3 => 2, 5 => 0, 6 => 1, 4 => 2]

$nearest = $multiBFS->findNearestSource($cityMap, $hospitals);
echo "Nearest hospital for each location:\n";
print_r($nearest);
// [0 => 0, 1 => 0, 2 => 0, 3 => 0, 5 => 5, 6 => 5, 4 => 0]

BFS on 2D Grid

Common application of BFS for grid-based problems. Grids are a special type of graph where each cell is a vertex connected to its four (or eight) neighbors. BFS is ideal for grid problems because it naturally finds the shortest path in terms of number of moves, making it perfect for pathfinding, flood fill, and island counting problems.

<?php

declare(strict_types=1);

class GridBFS
{
    private const DIRECTIONS = [
        [-1, 0],  // Up
        [0, 1],   // Right
        [1, 0],   // Down
        [0, -1]   // Left
    ];

    // Find shortest path in grid (1 = walkable, 0 = obstacle)
    public function shortestPath(array $grid, array $start, array $end): ?int
    {
        $rows = count($grid);
        $cols = count($grid[0]);
        $visited = [];

        $queue = [[$start[0], $start[1], 0]];  // [row, col, distance]
        $visited["{$start[0]},{$start[1]}"] = true;

        while (!empty($queue)) {
            [$row, $col, $distance] = array_shift($queue);

            // Check if reached end
            if ($row === $end[0] && $col === $end[1]) {
                return $distance;
            }

            // Try all 4 directions
            foreach (self::DIRECTIONS as [$dr, $dc]) {
                $newRow = $row + $dr;
                $newCol = $col + $dc;
                $key = "$newRow,$newCol";

                // Check bounds
                if ($newRow >= 0 && $newRow < $rows &&
                    $newCol >= 0 && $newCol < $cols &&
                    $grid[$newRow][$newCol] === 1 &&
                    !isset($visited[$key])) {

                    $visited[$key] = true;
                    $queue[] = [$newRow, $newCol, $distance + 1];
                }
            }
        }

        return null;  // No path found
    }

    // Flood fill (paint all connected cells)
    public function floodFill(array $grid, int $row, int $col, int $newColor): array
    {
        $rows = count($grid);
        $cols = count($grid[0]);
        $originalColor = $grid[$row][$col];

        if ($originalColor === $newColor) {
            return $grid;
        }

        $queue = [[$row, $col]];
        $grid[$row][$col] = $newColor;

        while (!empty($queue)) {
            [$r, $c] = array_shift($queue);

            foreach (self::DIRECTIONS as [$dr, $dc]) {
                $newRow = $r + $dr;
                $newCol = $c + $dc;

                if ($newRow >= 0 && $newRow < $rows &&
                    $newCol >= 0 && $newCol < $cols &&
                    $grid[$newRow][$newCol] === $originalColor) {

                    $grid[$newRow][$newCol] = $newColor;
                    $queue[] = [$newRow, $newCol];
                }
            }
        }

        return $grid;
    }

    // Count islands (connected 1s)
    public function countIslands(array $grid): int
    {
        $rows = count($grid);
        $cols = count($grid[0]);
        $visited = [];
        $count = 0;

        for ($row = 0; $row < $rows; $row++) {
            for ($col = 0; $col < $cols; $col++) {
                $key = "$row,$col";

                if ($grid[$row][$col] === 1 && !isset($visited[$key])) {
                    $this->bfsIsland($grid, $row, $col, $visited);
                    $count++;
                }
            }
        }

        return $count;
    }

    private function bfsIsland(array $grid, int $startRow, int $startCol, array &$visited): void
    {
        $rows = count($grid);
        $cols = count($grid[0]);
        $queue = [[$startRow, $startCol]];
        $visited["$startRow,$startCol"] = true;

        while (!empty($queue)) {
            [$row, $col] = array_shift($queue);

            foreach (self::DIRECTIONS as [$dr, $dc]) {
                $newRow = $row + $dr;
                $newCol = $col + $dc;
                $key = "$newRow,$newCol";

                if ($newRow >= 0 && $newRow < $rows &&
                    $newCol >= 0 && $newCol < $cols &&
                    $grid[$newRow][$newCol] === 1 &&
                    !isset($visited[$key])) {

                    $visited[$key] = true;
                    $queue[] = [$newRow, $newCol];
                }
            }
        }
    }
}

// Example - Grid pathfinding
$grid = [
    [1, 1, 0, 1],
    [1, 0, 1, 1],
    [1, 1, 1, 0],
    [0, 1, 1, 1]
];

$gridBFS = new GridBFS();
$distance = $gridBFS->shortestPath($grid, [0, 0], [3, 3]);
echo "Shortest path length: $distance\n";  // 6

// Example - Island counting
$islandGrid = [
    [1, 1, 0, 0, 0],
    [1, 1, 0, 0, 1],
    [0, 0, 0, 1, 1],
    [0, 0, 0, 0, 0],
    [1, 0, 1, 0, 1]
];

echo "Number of islands: " . $gridBFS->countIslands($islandGrid) . "\n";  // 5

Finding Nodes at Distance K

BFS naturally finds all nodes at a specific distance from a source. This is useful for social network analysis (friends within N degrees), network routing (nodes within N hops), and game mechanics (units within range).

<?php

declare(strict_types=1);

class NodesAtDistanceK
{
    // Find all nodes exactly K distance away from start
    public function findNodesAtDistance(array $graph, int $start, int $k): array
    {
        if ($k === 0) {
            return [$start];
        }

        $distances = [$start => 0];
        $queue = [$start];
        $result = [];

        while (!empty($queue)) {
            $vertex = array_shift($queue);
            $currentDistance = $distances[$vertex];

            if ($currentDistance === $k) {
                $result[] = $vertex;
                continue; // Don't explore further
            }

            foreach ($graph[$vertex] ?? [] as $neighbor) {
                if (!isset($distances[$neighbor])) {
                    $distances[$neighbor] = $currentDistance + 1;
                    $queue[] = $neighbor;
                }
            }
        }

        return $result;
    }

    // Find all nodes within distance K (inclusive)
    public function findNodesWithinDistance(array $graph, int $start, int $k): array
    {
        $distances = [$start => 0];
        $queue = [$start];
        $result = [$start]; // Include start if k >= 0

        while (!empty($queue)) {
            $vertex = array_shift($queue);
            $currentDistance = $distances[$vertex];

            if ($currentDistance < $k) {
                foreach ($graph[$vertex] ?? [] as $neighbor) {
                    if (!isset($distances[$neighbor])) {
                        $distances[$neighbor] = $currentDistance + 1;
                        $queue[] = $neighbor;
                        $result[] = $neighbor;
                    }
                }
            }
        }

        return $result;
    }
}

// Example - Social network: find friends within 2 degrees
$socialNetwork = [
    'Alice' => ['Bob', 'Charlie'],
    'Bob' => ['Alice', 'David', 'Eve'],
    'Charlie' => ['Alice', 'Frank'],
    'David' => ['Bob', 'Grace'],
    'Eve' => ['Bob'],
    'Frank' => ['Charlie'],
    'Grace' => ['David']
];

$finder = new NodesAtDistanceK();
$friendsAtDistance2 = $finder->findNodesAtDistance($socialNetwork, 'Alice', 2);
print_r($friendsAtDistance2);
// ['David', 'Eve', 'Frank'] - friends of friends

$friendsWithin2 = $finder->findNodesWithinDistance($socialNetwork, 'Alice', 2);
print_r($friendsWithin2);
// ['Alice', 'Bob', 'Charlie', 'David', 'Eve', 'Frank'] - all within 2 degrees

BFS for Tree Diameter

The diameter of a tree is the longest path between any two nodes. We can find it using two BFS passes: first find the farthest node from any node, then find the farthest node from that node. The distance between these two nodes is the diameter.

<?php

declare(strict_types=1);

class TreeDiameterBFS
{
    // Find diameter of tree using two BFS passes
    public function findDiameter(array $tree, int $start): int
    {
        // First BFS: Find farthest node from start
        [$farthestNode, $distance] = $this->findFarthestNode($tree, $start);

        // Second BFS: Find farthest node from the farthest node
        [, $diameter] = $this->findFarthestNode($tree, $farthestNode);

        return $diameter;
    }

    // Find the farthest node and its distance from start
    private function findFarthestNode(array $tree, int $start): array
    {
        $distances = [$start => 0];
        $queue = [$start];
        $farthestNode = $start;
        $maxDistance = 0;

        while (!empty($queue)) {
            $vertex = array_shift($queue);
            $currentDistance = $distances[$vertex];

            if ($currentDistance > $maxDistance) {
                $maxDistance = $currentDistance;
                $farthestNode = $vertex;
            }

            foreach ($tree[$vertex] ?? [] as $neighbor) {
                if (!isset($distances[$neighbor])) {
                    $distances[$neighbor] = $currentDistance + 1;
                    $queue[] = $neighbor;
                }
            }
        }

        return [$farthestNode, $maxDistance];
    }

    // Find the actual diameter path
    public function findDiameterPath(array $tree, int $start): array
    {
        // Find one end of diameter
        [$end1] = $this->findFarthestNode($tree, $start);

        // Find path to farthest node from end1
        $path = $this->findPathToFarthest($tree, $end1);

        return $path;
    }

    private function findPathToFarthest(array $tree, int $start): array
    {
        $distances = [$start => 0];
        $parent = [$start => null];
        $queue = [$start];
        $farthestNode = $start;
        $maxDistance = 0;

        while (!empty($queue)) {
            $vertex = array_shift($queue);
            $currentDistance = $distances[$vertex];

            if ($currentDistance > $maxDistance) {
                $maxDistance = $currentDistance;
                $farthestNode = $vertex;
            }

            foreach ($tree[$vertex] ?? [] as $neighbor) {
                if (!isset($distances[$neighbor])) {
                    $distances[$neighbor] = $currentDistance + 1;
                    $parent[$neighbor] = $vertex;
                    $queue[] = $neighbor;
                }
            }
        }

        // Reconstruct path
        $path = [];
        $current = $farthestNode;
        while ($current !== null) {
            array_unshift($path, $current);
            $current = $parent[$current] ?? null;
        }

        return $path;
    }
}

// Example - Tree structure
$tree = [
    0 => [1, 2],
    1 => [0, 3, 4],
    2 => [0, 5],
    3 => [1],
    4 => [1],
    5 => [2]
];

$diameterFinder = new TreeDiameterBFS();
echo "Tree diameter: " . $diameterFinder->findDiameter($tree, 0) . "\n";  // 4
$path = $diameterFinder->findDiameterPath($tree, 0);
echo "Diameter path: " . implode(' → ', $path) . "\n";  // 3 → 1 → 0 → 2 → 5

Shortest Cycle Detection

BFS can find the shortest cycle in a graph by checking if a neighbor has been visited and is not the parent. For undirected graphs, we need to track parent to avoid false positives.

<?php

declare(strict_types=1);

class ShortestCycleBFS
{
    // Find shortest cycle length in undirected graph
    public function findShortestCycle(array $graph): ?int
    {
        $minCycle = null;

        // Try BFS from each vertex
        foreach (array_keys($graph) as $start) {
            $cycleLength = $this->bfsCycle($graph, $start);
            if ($cycleLength !== null) {
                $minCycle = $minCycle === null ? $cycleLength : min($minCycle, $cycleLength);
            }
        }

        return $minCycle;
    }

    private function bfsCycle(array $graph, int $start): ?int
    {
        $distances = [$start => 0];
        $parent = [$start => -1]; // Use -1 to indicate no parent
        $queue = [$start];
        $minCycle = null;

        while (!empty($queue)) {
            $vertex = array_shift($queue);
            $currentDistance = $distances[$vertex];

            foreach ($graph[$vertex] ?? [] as $neighbor) {
                if (!isset($distances[$neighbor])) {
                    // New vertex
                    $distances[$neighbor] = $currentDistance + 1;
                    $parent[$neighbor] = $vertex;
                    $queue[] = $neighbor;
                } elseif ($parent[$vertex] !== $neighbor) {
                    // Found a cycle (neighbor is visited but not parent)
                    $cycleLength = $distances[$vertex] + $distances[$neighbor] + 1;
                    $minCycle = $minCycle === null ? $cycleLength : min($minCycle, $cycleLength);
                }
            }
        }

        return $minCycle;
    }

    // Find shortest cycle in directed graph
    public function findShortestCycleDirected(array $graph): ?int
    {
        $minCycle = null;

        foreach (array_keys($graph) as $start) {
            $cycleLength = $this->bfsCycleDirected($graph, $start);
            if ($cycleLength !== null) {
                $minCycle = $minCycle === null ? $cycleLength : min($minCycle, $cycleLength);
            }
        }

        return $minCycle;
    }

    private function bfsCycleDirected(array $graph, int $start): ?int
    {
        $distances = [$start => 0];
        $queue = [$start];
        $minCycle = null;

        while (!empty($queue)) {
            $vertex = array_shift($queue);
            $currentDistance = $distances[$vertex];

            foreach ($graph[$vertex] ?? [] as $neighbor) {
                if ($neighbor === $start) {
                    // Found cycle back to start
                    $cycleLength = $currentDistance + 1;
                    $minCycle = $minCycle === null ? $cycleLength : min($minCycle, $cycleLength);
                } elseif (!isset($distances[$neighbor])) {
                    $distances[$neighbor] = $currentDistance + 1;
                    $queue[] = $neighbor;
                }
            }
        }

        return $minCycle;
    }
}

// Example - Undirected graph with cycles
$graph = [
    0 => [1, 2],
    1 => [0, 2, 3],
    2 => [0, 1],
    3 => [1, 4],
    4 => [3]
];

$cycleFinder = new ShortestCycleBFS();
echo "Shortest cycle length: " . $cycleFinder->findShortestCycle($graph) . "\n";  // 3 (0-1-2-0)

// Example - Directed graph
$directedGraph = [
    0 => [1],
    1 => [2],
    2 => [0, 3],
    3 => [4],
    4 => [2]
];

echo "Shortest cycle (directed): " . $cycleFinder->findShortestCycleDirected($directedGraph) . "\n";  // 3 (0-1-2-0)

BFS on Directed vs Undirected Graphs

BFS works on both directed and undirected graphs, but there are important differences in behavior and applications.

<?php

declare(strict_types=1);

class BFSDirectedUndirected
{
    // Key differences when using BFS:

    public function compare(): array
    {
        return [
            'Undirected Graphs' => [
                'Neighbor Access' => 'Both directions accessible',
                'Cycle Detection' => 'Need parent tracking to avoid false positives',
                'Connected Components' => 'All reachable vertices form one component',
                'Path Finding' => 'Bidirectional paths always exist',
                'Use Case' => 'Social networks, road networks, friendship graphs'
            ],
            'Directed Graphs' => [
                'Neighbor Access' => 'Only outgoing edges accessible',
                'Cycle Detection' => 'Can detect cycles by checking if start is reachable',
                'Connected Components' => 'Need strongly connected components (SCC) algorithm',
                'Path Finding' => 'Paths only exist in direction of edges',
                'Use Case' => 'Dependency graphs, web links, state machines'
            ]
        ];
    }

    // BFS on undirected graph - can traverse both ways
    public function bfsUndirected(array $graph, int $start): array
    {
        $visited = [$start => true];
        $result = [$start];
        $queue = [$start];

        while (!empty($queue)) {
            $vertex = array_shift($queue);

            // In undirected graph, neighbors array contains all connected vertices
            foreach ($graph[$vertex] ?? [] as $neighbor) {
                if (!isset($visited[$neighbor])) {
                    $visited[$neighbor] = true;
                    $result[] = $neighbor;
                    $queue[] = $neighbor;
                }
            }
        }

        return $result;
    }

    // BFS on directed graph - only follows edge directions
    public function bfsDirected(array $graph, int $start): array
    {
        $visited = [$start => true];
        $result = [$start];
        $queue = [$start];

        while (!empty($queue)) {
            $vertex = array_shift($queue);

            // In directed graph, only follow outgoing edges
            foreach ($graph[$vertex] ?? [] as $neighbor) {
                if (!isset($visited[$neighbor])) {
                    $visited[$neighbor] = true;
                    $result[] = $neighbor;
                    $queue[] = $neighbor;
                }
            }
        }

        return $result;
    }

    // Check reachability in directed graph (one-way)
    public function isReachable(array $graph, int $from, int $to): bool
    {
        $visited = [$from => true];
        $queue = [$from];

        while (!empty($queue)) {
            $vertex = array_shift($queue);

            if ($vertex === $to) {
                return true;
            }

            foreach ($graph[$vertex] ?? [] as $neighbor) {
                if (!isset($visited[$neighbor])) {
                    $visited[$neighbor] = true;
                    $queue[] = $neighbor;
                }
            }
        }

        return false;
    }
}

// Example - Undirected graph
$undirected = [
    0 => [1, 2],
    1 => [0, 2],  // Bidirectional
    2 => [0, 1]
];

// Example - Directed graph
$directed = [
    0 => [1, 2],
    1 => [2],     // One-way only
    2 => []        // No outgoing edges
];

$bfs = new BFSDirectedUndirected();
print_r($bfs->bfsUndirected($undirected, 0));  // [0, 1, 2]
print_r($bfs->bfsDirected($directed, 0));     // [0, 1, 2]
echo $bfs->isReachable($directed, 0, 2) ? "Reachable\n" : "Not reachable\n";  // Reachable
echo $bfs->isReachable($directed, 2, 0) ? "Reachable\n" : "Not reachable\n";  // Not reachable

Word Ladder Problem

Transform one word to another changing one letter at a time. This classic problem models words as vertices in a graph, where two words are connected if they differ by exactly one letter. BFS finds the shortest transformation sequence, making it perfect for this problem since we want the minimum number of steps.

<?php

declare(strict_types=1);

class WordLadder
{
    // Find shortest transformation sequence
    public function ladderLength(string $beginWord, string $endWord, array $wordList): ?int
    {
        $wordSet = array_flip($wordList);

        if (!isset($wordSet[$endWord])) {
            return null;  // End word not in dictionary
        }

        $queue = [[$beginWord, 1]];  // [word, steps]
        $visited = [$beginWord => true];

        while (!empty($queue)) {
            [$word, $steps] = array_shift($queue);

            if ($word === $endWord) {
                return $steps;
            }

            // Try changing each letter
            for ($i = 0; $i < strlen($word); $i++) {
                for ($c = ord('a'); $c <= ord('z'); $c++) {
                    $newWord = substr($word, 0, $i) . chr($c) . substr($word, $i + 1);

                    if (isset($wordSet[$newWord]) && !isset($visited[$newWord])) {
                        $visited[$newWord] = true;
                        $queue[] = [$newWord, $steps + 1];
                    }
                }
            }
        }

        return null;  // No transformation sequence found
    }

    // Find the actual transformation sequence
    public function findLadder(string $beginWord, string $endWord, array $wordList): ?array
    {
        $wordSet = array_flip($wordList);

        if (!isset($wordSet[$endWord])) {
            return null;
        }

        $queue = [[$beginWord, [$beginWord]]];
        $visited = [$beginWord => true];

        while (!empty($queue)) {
            [$word, $path] = array_shift($queue);

            if ($word === $endWord) {
                return $path;
            }

            for ($i = 0; $i < strlen($word); $i++) {
                for ($c = ord('a'); $c <= ord('z'); $c++) {
                    $newWord = substr($word, 0, $i) . chr($c) . substr($word, $i + 1);

                    if (isset($wordSet[$newWord]) && !isset($visited[$newWord])) {
                        $visited[$newWord] = true;
                        $newPath = array_merge($path, [$newWord]);
                        $queue[] = [$newWord, $newPath];
                    }
                }
            }
        }

        return null;
    }
}

// Example
$ladder = new WordLadder();
$wordList = ['hot', 'dot', 'dog', 'lot', 'log', 'cog'];

$length = $ladder->ladderLength('hit', 'cog', $wordList);
echo "Ladder length: $length\n";  // 5

$sequence = $ladder->findLadder('hit', 'cog', $wordList);
echo "Transformation: " . implode(' -> ', $sequence) . "\n";
// hit -> hot -> dot -> dog -> cog

Complexity Analysis

Operation	Time Complexity	Space Complexity
BFS Traversal	O(V + E)	O(V)
Shortest Path	O(V + E)	O(V)
All Shortest Paths	O(V + E + P)	O(V + P)
Bidirectional BFS	O(b^(d/2))	O(b^(d/2))
Bipartite Check	O(V + E)	O(V)
Kahn’s Topological Sort	O(V + E)	O(V)
0-1 BFS	O(V + E)	O(V)
Multi-source BFS	O(V + E)	O(V)
Grid BFS (m×n grid)	O(m × n)	O(m × n)
Nodes at Distance K	O(V + E)	O(V)
Tree Diameter (2 BFS)	O(V + E)	O(V)
Shortest Cycle	O(V × (V + E))	O(V)

Where:

V = number of vertices
E = number of edges
P = number of shortest paths (for all shortest paths)
b = branching factor (for bidirectional BFS)
d = depth/distance (for bidirectional BFS)
m, n = grid dimensions

BFS vs DFS Comparison

<?php

declare(strict_types=1);

class BFSvsDFS
{
    public function compare(): array
    {
        return [
            'Data Structure' => [
                'BFS' => 'Queue (FIFO)',
                'DFS' => 'Stack (LIFO) or recursion'
            ],
            'Exploration' => [
                'BFS' => 'Level by level (breadth)',
                'DFS' => 'Branch by branch (depth)'
            ],
            'Shortest Path' => [
                'BFS' => 'Guaranteed shortest (unweighted)',
                'DFS' => 'Not guaranteed shortest'
            ],
            'Memory' => [
                'BFS' => 'O(width) - can be large',
                'DFS' => 'O(height) - usually smaller'
            ],
            'Best For' => [
                'BFS' => 'Shortest path, level-order, nearby solutions',
                'DFS' => 'Topological sort, cycles, exhaustive search'
            ],
            'Complete' => [
                'BFS' => 'Yes (finds solution if exists)',
                'DFS' => 'No (can get stuck in infinite path)'
            ]
        ];
    }
}

Framework Integration Examples

Laravel Graph Service with BFS

Real-world integration of BFS in a Laravel application:

<?php

declare(strict_types=1);

namespace App\Services;

use Illuminate\Support\Collection;
use Illuminate\Support\Facades\Cache;
use App\Models\User;

/**
 * Graph-based service using BFS for social features
 */
class SocialGraphService
{
    // Find shortest connection path between two users
    public function findConnectionPath(int $userId1, int $userId2): ?array
    {
        // Cache key for this connection path
        $cacheKey = "connection_path:{$userId1}:{$userId2}";

        return Cache::remember($cacheKey, now()->addHours(24), function() use ($userId1, $userId2) {
            return $this->bfsConnectionPath($userId1, $userId2);
        });
    }

    private function bfsConnectionPath(int $startId, int $endId): ?array
    {
        if ($startId === $endId) {
            return [User::find($startId)];
        }

        $visited = [$startId => true];
        $parent = [$startId => null];
        $queue = [$startId];

        while (!empty($queue)) {
            $currentId = array_shift($queue);

            // Get friends of current user
            $friends = User::find($currentId)
                ->friends()
                ->pluck('id')
                ->toArray();

            foreach ($friends as $friendId) {
                if (!isset($visited[$friendId])) {
                    $visited[$friendId] = true;
                    $parent[$friendId] = $currentId;
                    $queue[] = $friendId;

                    // Found the target!
                    if ($friendId === $endId) {
                        return $this->reconstructPath($parent, $startId, $endId);
                    }
                }
            }
        }

        return null; // No connection found
    }

    private function reconstructPath(array $parent, int $start, int $end): array
    {
        $path = [];
        $current = $end;

        while ($current !== null) {
            array_unshift($path, User::find($current));
            $current = $parent[$current];
        }

        return $path;
    }

    // Calculate degrees of separation
    public function getDegreesOfSeparation(int $userId1, int $userId2): int
    {
        $path = $this->findConnectionPath($userId1, $userId2);

        if ($path === null) {
            return -1; // Not connected
        }

        return count($path) - 1; // Number of hops
    }

    // Find all users within N degrees
    public function findUsersWithinDistance(int $userId, int $maxDistance): Collection
    {
        $visited = [$userId => 0]; // user_id => distance
        $queue = [[$userId, 0]]; // [user_id, distance]
        $result = collect();

        while (!empty($queue)) {
            [$currentId, $distance] = array_shift($queue);

            if ($distance <= $maxDistance && $currentId !== $userId) {
                $result->push([
                    'user' => User::find($currentId),
                    'distance' => $distance
                ]);
            }

            if ($distance < $maxDistance) {
                $friends = User::find($currentId)
                    ->friends()
                    ->pluck('id')
                    ->toArray();

                foreach ($friends as $friendId) {
                    if (!isset($visited[$friendId])) {
                        $visited[$friendId] = $distance + 1;
                        $queue[] = [$friendId, $distance + 1];
                    }
                }
            }
        }

        return $result;
    }

    // Recommend friends (friends of friends not yet connected)
    public function recommendFriends(int $userId, int $limit = 10): Collection
    {
        $user = User::find($userId);
        $directFriends = $user->friends()->pluck('id')->toArray();
        $recommendations = [];

        // BFS to explore 2 levels deep
        $visited = array_flip(array_merge([$userId], $directFriends));
        $queue = [];

        // Start from direct friends
        foreach ($directFriends as $friendId) {
            $queue[] = [$friendId, 1];
        }

        while (!empty($queue)) {
            [$currentId, $level] = array_shift($queue);

            if ($level === 2) {
                // This is a friend-of-friend
                if (!isset($visited[$currentId])) {
                    $mutualFriends = $this->countMutualFriends($userId, $currentId);

                    $recommendations[] = [
                        'user' => User::find($currentId),
                        'mutual_friends' => $mutualFriends,
                        'score' => $mutualFriends // Can be enhanced with more factors
                    ];

                    $visited[$currentId] = true;

                    if (count($recommendations) >= $limit * 2) {
                        break; // Early termination
                    }
                }
            }

            if ($level < 2) {
                $friends = User::find($currentId)
                    ->friends()
                    ->pluck('id')
                    ->toArray();

                foreach ($friends as $friendId) {
                    if (!isset($visited[$friendId])) {
                        $queue[] = [$friendId, $level + 1];
                    }
                }
            }
        }

        // Sort by score and return top N
        usort($recommendations, fn($a, $b) => $b['score'] <=> $a['score']);

        return collect(array_slice($recommendations, 0, $limit));
    }

    private function countMutualFriends(int $userId1, int $userId2): int
    {
        $friends1 = User::find($userId1)->friends()->pluck('id')->toArray();
        $friends2 = User::find($userId2)->friends()->pluck('id')->toArray();

        return count(array_intersect($friends1, $friends2));
    }

    // Find network influencers (users with high closeness centrality)
    public function findInfluencers(int $limit = 10): Collection
    {
        $users = User::all();
        $centrality = [];

        foreach ($users as $user) {
            $distances = $this->bfsDistances($user->id);
            $totalDistance = array_sum($distances);
            $reachable = count($distances) - 1; // Exclude self

            $centrality[$user->id] = [
                'user' => $user,
                'centrality' => $reachable > 0 ? $reachable / $totalDistance : 0,
                'reach' => $reachable
            ];
        }

        // Sort by centrality
        usort($centrality, fn($a, $b) => $b['centrality'] <=> $a['centrality']);

        return collect(array_slice($centrality, 0, $limit));
    }

    private function bfsDistances(int $startId): array
    {
        $distances = [$startId => 0];
        $queue = [$startId];

        while (!empty($queue)) {
            $currentId = array_shift($queue);
            $currentDist = $distances[$currentId];

            $friends = User::find($currentId)
                ->friends()
                ->pluck('id')
                ->toArray();

            foreach ($friends as $friendId) {
                if (!isset($distances[$friendId])) {
                    $distances[$friendId] = $currentDist + 1;
                    $queue[] = $friendId;
                }
            }
        }

        return $distances;
    }
}

// Usage in Laravel Controller
namespace App\Http\Controllers;

use App\Services\SocialGraphService;
use Illuminate\Http\Request;

class SocialGraphController extends Controller
{
    public function __construct(
        private SocialGraphService $graphService
    ) {}

    public function connectionPath(Request $request)
    {
        $userId1 = $request->user()->id;
        $userId2 = $request->input('user_id');

        $path = $this->graphService->findConnectionPath($userId1, $userId2);

        if ($path === null) {
            return response()->json([
                'connected' => false,
                'message' => 'No connection found'
            ]);
        }

        return response()->json([
            'connected' => true,
            'degrees' => count($path) - 1,
            'path' => array_map(fn($user) => [
                'id' => $user->id,
                'name' => $user->name
            ], $path)
        ]);
    }

    public function recommendations(Request $request)
    {
        $userId = $request->user()->id;
        $limit = $request->input('limit', 10);

        $recommendations = $this->graphService->recommendFriends($userId, $limit);

        return response()->json([
            'recommendations' => $recommendations->map(fn($rec) => [
                'user' => [
                    'id' => $rec['user']->id,
                    'name' => $rec['user']->name,
                    'avatar' => $rec['user']->avatar_url
                ],
                'mutual_friends' => $rec['mutual_friends'],
                'score' => $rec['score']
            ])
        ]);
    }

    public function nearby(Request $request)
    {
        $userId = $request->user()->id;
        $distance = $request->input('distance', 2);

        $users = $this->graphService->findUsersWithinDistance($userId, $distance);

        return response()->json([
            'users' => $users->map(fn($item) => [
                'user' => [
                    'id' => $item['user']->id,
                    'name' => $item['user']->name
                ],
                'distance' => $item['distance']
            ])
        ]);
    }

    public function influencers()
    {
        $influencers = $this->graphService->findInfluencers(20);

        return response()->json([
            'influencers' => $influencers->map(fn($item) => [
                'user' => [
                    'id' => $item['user']->id,
                    'name' => $item['user']->name
                ],
                'centrality_score' => round($item['centrality'], 4),
                'reach' => $item['reach']
            ])
        ]);
    }
}

// Routes (routes/api.php)
/*
Route::middleware('auth:sanctum')->group(function () {
    Route::get('/social/connection/{user_id}', [SocialGraphController::class, 'connectionPath']);
    Route::get('/social/recommendations', [SocialGraphController::class, 'recommendations']);
    Route::get('/social/nearby', [SocialGraphController::class, 'nearby']);
    Route::get('/social/influencers', [SocialGraphController::class, 'influencers']);
});
*/

Symfony Content Recommendation System

<?php

declare(strict_types=1);

namespace App\Service;

use Doctrine\ORM\EntityManagerInterface;
use App\Entity\Content;
use App\Entity\User;
use Symfony\Contracts\Cache\CacheInterface;
use Symfony\Contracts\Cache\ItemInterface;

/**
 * BFS-based content recommendation system
 */
class ContentRecommendationService
{
    public function __construct(
        private EntityManagerInterface $em,
        private CacheInterface $cache
    ) {}

    // Find related content through user interaction graph
    public function findRelatedContent(int $contentId, int $limit = 10): array
    {
        return $this->cache->get(
            "related_content_{$contentId}_{$limit}",
            function (ItemInterface $item) use ($contentId, $limit) {
                $item->expiresAfter(3600); // 1 hour cache

                return $this->bfsRelatedContent($contentId, $limit);
            }
        );
    }

    private function bfsRelatedContent(int $startContentId, int $limit): array
    {
        $visited = [$startContentId => true];
        $queue = [[$startContentId, 0]]; // [content_id, distance]
        $related = [];

        // Build graph: content -> users who viewed it -> other content they viewed
        while (!empty($queue) && count($related) < $limit) {
            [$contentId, $distance] = array_shift($queue);

            if ($distance > 0 && $distance <= 2) {
                $content = $this->em->find(Content::class, $contentId);
                if ($content) {
                    $related[] = [
                        'content' => $content,
                        'distance' => $distance,
                        'score' => $this->calculateRelevanceScore($startContentId, $contentId)
                    ];
                }
            }

            if ($distance < 2) {
                // Find users who viewed this content
                $viewers = $this->em->getRepository(User::class)
                    ->createQueryBuilder('u')
                    ->innerJoin('u.viewedContent', 'c')
                    ->where('c.id = :contentId')
                    ->setParameter('contentId', $contentId)
                    ->getQuery()
                    ->getResult();

                // Find other content these users viewed
                foreach ($viewers as $viewer) {
                    $otherContent = $viewer->getViewedContent();

                    foreach ($otherContent as $content) {
                        if (!isset($visited[$content->getId()])) {
                            $visited[$content->getId()] = true;
                            $queue[] = [$content->getId(), $distance + 1];
                        }
                    }
                }
            }
        }

        // Sort by relevance score
        usort($related, fn($a, $b) => $b['score'] <=> $a['score']);

        return array_slice($related, 0, $limit);
    }

    private function calculateRelevanceScore(int $sourceId, int $targetId): float
    {
        // Calculate based on multiple factors
        $sharedViewers = $this->countSharedViewers($sourceId, $targetId);
        $categoryMatch = $this->haveSameCategory($sourceId, $targetId) ? 1.5 : 1.0;
        $recency = $this->getRecencyBoost($targetId);

        return $sharedViewers * $categoryMatch * $recency;
    }

    private function countSharedViewers(int $contentId1, int $contentId2): int
    {
        return (int) $this->em->createQueryBuilder()
            ->select('COUNT(DISTINCT u.id)')
            ->from(User::class, 'u')
            ->innerJoin('u.viewedContent', 'c1')
            ->innerJoin('u.viewedContent', 'c2')
            ->where('c1.id = :id1 AND c2.id = :id2')
            ->setParameter('id1', $contentId1)
            ->setParameter('id2', $contentId2)
            ->getQuery()
            ->getSingleScalarResult();
    }

    private function haveSameCategory(int $contentId1, int $contentId2): bool
    {
        $content1 = $this->em->find(Content::class, $contentId1);
        $content2 = $this->em->find(Content::class, $contentId2);

        return $content1 && $content2 &&
               $content1->getCategory() === $content2->getCategory();
    }

    private function getRecencyBoost(int $contentId): float
    {
        $content = $this->em->find(Content::class, $contentId);
        if (!$content) return 1.0;

        $daysSincePublished = (new \DateTime())->diff($content->getPublishedAt())->days;

        // Boost recent content
        if ($daysSincePublished < 7) return 1.5;
        if ($daysSincePublished < 30) return 1.2;
        return 1.0;
    }
}

Practical Applications

<?php

declare(strict_types=1);

class FriendSuggestions
{
    // Find friends of friends (2 hops away)
    public function suggestFriends(array $network, string $user): array
    {
        $suggestions = [];
        $visited = [$user => true];
        $queue = [[$user, 0]];  // [user, distance]

        while (!empty($queue)) {
            [$current, $distance] = array_shift($queue);

            if ($distance === 2) {
                // Friends of friends (not already friends)
                $suggestions[] = $current;
                continue;  // Don't explore further
            }

            foreach ($network[$current] ?? [] as $friend) {
                if (!isset($visited[$friend])) {
                    $visited[$friend] = true;
                    $queue[] = [$friend, $distance + 1];
                }
            }
        }

        return $suggestions;
    }
}

2. Shortest Route in City Map

<?php

declare(strict_types=1);

class CityRouter
{
    public function findShortestRoute(
        array $cityMap,
        string $start,
        string $destination
    ): ?array {
        if ($start === $destination) {
            return [$start];
        }

        $visited = [$start => true];
        $parent = [$start => null];
        $queue = [$start];

        while (!empty($queue)) {
            $location = array_shift($queue);

            foreach ($cityMap[$location] ?? [] as $neighbor) {
                if (!isset($visited[$neighbor])) {
                    $visited[$neighbor] = true;
                    $parent[$neighbor] = $location;
                    $queue[] = $neighbor;

                    if ($neighbor === $destination) {
                        return $this->buildPath($parent, $start, $destination);
                    }
                }
            }
        }

        return null;
    }

    private function buildPath(array $parent, string $start, string $end): array
    {
        $path = [];
        $current = $end;

        while ($current !== null) {
            array_unshift($path, $current);
            $current = $parent[$current];
        }

        return $path;
    }
}

Best Practices

Use Queue for BFS
- Always use FIFO queue (array_shift + array_push)
- Don’t use stack (would be DFS)
Mark as Visited When Enqueued
- Prevents duplicates in queue
- More efficient than checking during dequeue
Track Parent/Distance
- For path reconstruction, maintain parent array
- For distances, maintain distance array
Handle Disconnected Graphs
- Loop through all vertices
- Start BFS from unvisited vertices

Practice Exercises

Exercise 1: Shortest Bridge

Goal: Find the shortest bridge connecting two islands in a 2D grid.

Requirements:

Grid contains two islands (connected 1s) separated by water (0s)
Use multi-source BFS starting from all cells of one island
Find minimum distance to reach any cell of the other island
Return the number of cells in the shortest bridge

Validation: Test with a grid where islands are separated by water:

$grid = [
    [1, 1, 0, 0, 0],
    [1, 0, 0, 0, 0],
    [1, 0, 0, 0, 1],
    [0, 0, 0, 0, 1],
    [0, 0, 0, 1, 1]
];
// Expected: shortest bridge length is 2

Exercise 2: Rotting Oranges

Goal: Find minimum time for all fresh oranges to rot.

Requirements:

Grid contains: 0 (empty), 1 (fresh orange), 2 (rotten orange)
Rotten oranges rot adjacent fresh oranges each minute
Use multi-source BFS starting from all rotten oranges
Return minimum minutes to rot all oranges, or -1 if impossible

Validation: Test with grid containing fresh and rotten oranges:

$grid = [
    [2, 1, 1],
    [1, 1, 0],
    [0, 1, 1]
];
// Expected: 4 minutes

Exercise 3: Binary Tree Level Order Traversal

Goal: Return tree nodes organized by level.

Requirements:

Implement BFS on binary tree structure
Return array of arrays: each inner array contains nodes at that level
Handle empty trees gracefully

Validation: Test with a binary tree:

// Tree:     3
//         / \
//        9   20
//           /  \
//          15   7
// Expected: [[3], [9, 20], [15, 7]]

Exercise 4: Open the Lock

Goal: Find minimum turns to open a 4-digit lock.

Requirements:

Lock has 4 wheels, each 0-9
Each turn changes one wheel by ±1 (wraps around: 9→0, 0→9)
Avoid deadend combinations (provided in array)
Use BFS to find shortest path from “0000” to target

Validation: Test with deadends and target:

$deadends = ["0201", "0101", "0102", "1212", "2002"];
$target = "0202";
// Expected: 6 turns

Exercise 5: Word Ladder II

Goal: Find all shortest transformation sequences between two words.

Requirements:

Extend the Word Ladder problem to find ALL shortest paths
Use BFS to find shortest distance, then DFS to reconstruct all paths
Return all valid transformation sequences

Validation: Test with word list:

$wordList = ["hot", "dot", "dog", "lot", "log", "cog"];
// From "hit" to "cog"
// Expected: Multiple paths of length 5

Troubleshooting

Error: “Queue grows too large, memory exhausted”

Symptom: Fatal error: Allowed memory size exhausted when running BFS on large graphs

Cause: BFS stores entire levels in the queue, which can be very large for wide graphs (high branching factor)

Solution:

Use iterative deepening BFS (ID-BFS) for memory-constrained environments
Consider bidirectional BFS to reduce search space
For very wide graphs, DFS might be more memory-efficient:

// For wide graphs, consider DFS instead
if ($this->isWideGraph($graph)) {
    $dfs = new DFS();
    $result = $dfs->traverse($graph, $start);
} else {
    $bfs = new BFS();
    $result = $bfs->traverse($graph, $start);
}

Problem: BFS finds path but it’s not the shortest

Symptom: Path found by BFS is longer than expected

Cause: Not marking vertices as visited when enqueued, allowing them to be added multiple times

Solution: Always mark as visited when enqueuing, not when dequeuing:

// Correct - mark when enqueuing
foreach ($graph[$vertex] ?? [] as $neighbor) {
    if (!isset($visited[$neighbor])) {
        $visited[$neighbor] = true;  // Mark immediately
        $queue[] = $neighbor;
    }
}

// Wrong - marking when dequeuing allows duplicates
foreach ($graph[$vertex] ?? [] as $neighbor) {
    if (!isset($visited[$neighbor])) {
        $queue[] = $neighbor;  // Not marked yet!
    }
}
// Later when dequeuing:
$visited[$vertex] = true;  // Too late - duplicates already in queue

Problem: Infinite loop in BFS

Symptom: Algorithm runs forever, never terminates

Cause: Missing visited check or not resetting visited set between calls

Solution: Always check visited before enqueuing and reset between calls:

public function traverse(array $graph, int $start): array
{
    $visited = [];  // Reset visited
    $queue = [$start];
    $visited[$start] = true;  // Mark start immediately

    while (!empty($queue)) {
        $vertex = array_shift($queue);
        // Process vertex...

        foreach ($graph[$vertex] ?? [] as $neighbor) {
            if (!isset($visited[$neighbor])) {  // Always check
                $visited[$neighbor] = true;
                $queue[] = $neighbor;
            }
        }
    }
}

Problem: Wrong path reconstruction

Symptom: Reconstructed path is incorrect or incomplete

Cause: Not properly tracking parent relationships or incorrect path reconstruction logic

Solution: Ensure parent array is updated correctly and path reconstruction follows parent chain:

// Correct path reconstruction
private function reconstructPath(array $parent, int $start, int $end): array
{
    $path = [];
    $current = $end;

    while ($current !== null) {
        array_unshift($path, $current);
        $current = $parent[$current] ?? null;  // Use null coalescing
    }

    return $path;
}

// Ensure parent is set when discovering vertex
if (!isset($visited[$neighbor])) {
    $visited[$neighbor] = true;
    $parent[$neighbor] = $vertex;  // Set parent
    $queue[] = $neighbor;
}

Problem: BFS too slow for large graphs

Symptom: BFS takes too long on graphs with many vertices

Cause: Exploring entire graph when target might be nearby, or inefficient queue operations

Solution:

Use bidirectional BFS to reduce search space
Early termination when target is found
Use efficient queue implementation (SplQueue for large graphs):

// Use SplQueue for better performance
use SplQueue;

$queue = new SplQueue();
$queue->enqueue($start);

while (!$queue->isEmpty()) {
    $vertex = $queue->dequeue();
    // Process...
}

Problem: Multi-source BFS gives wrong distances

Symptom: Distances from multi-source BFS are incorrect

Cause: Not initializing all sources with distance 0, or processing sources incorrectly

Solution: Initialize all sources properly:

// Correct initialization
$distances = [];
$queue = [];

foreach ($sources as $source) {
    $distances[$source] = 0;  // All sources start at distance 0
    $queue[] = $source;
}

// Process normally - BFS will find nearest source automatically

Problem: Grid BFS out of bounds errors

Symptom: Undefined array key or index out of bounds errors in grid BFS

Cause: Not checking array bounds before accessing grid cells

Solution: Always validate bounds before accessing:

// Correct bounds checking
foreach (self::DIRECTIONS as [$dr, $dc]) {
    $newRow = $row + $dr;
    $newCol = $col + $dc;

    // Check bounds FIRST
    if ($newRow >= 0 && $newRow < $rows &&
        $newCol >= 0 && $newCol < $cols &&
        $grid[$newRow][$newCol] === 1 &&
        !isset($visited["$newRow,$newCol"])) {

        $visited["$newRow,$newCol"] = true;
        $queue[] = [$newRow, $newCol, $distance + 1];
    }
}

Key Takeaways

BFS explores graphs level by level using a queue
Guarantees shortest path in unweighted graphs
Time complexity: O(V + E), Space complexity: O(V)
Optimal for finding shortest paths, level-order traversal, nearby solutions
Uses more memory than DFS (stores entire level)
Essential for problems requiring minimum steps/distance
Natural choice for grid-based pathfinding
Can start from multiple sources simultaneously
Bidirectional BFS reduces search space from O(b^d) to O(b^(d/2))
Kahn’s algorithm provides intuitive BFS-based topological sort
Mark vertices as visited when enqueued, not when dequeued

Wrap-up

Congratulations! You’ve mastered Breadth-First Search, one of the most practical graph traversal algorithms. Here’s what you’ve accomplished:

✓ Implemented complete BFS traversal with level tracking
✓ Built visualization tools to understand BFS execution and queue operations
✓ Created shortest path finder for unweighted graphs
✓ Developed all shortest paths finder for path diversity analysis
✓ Implemented bidirectional BFS for efficient pathfinding
✓ Built bipartite graph detector using BFS coloring
✓ Implemented Kahn’s algorithm for BFS-based topological sort
✓ Created 0-1 BFS for graphs with binary edge weights
✓ Built multi-source BFS for finding nearest sources
✓ Implemented grid-based BFS for pathfinding and flood fill
✓ Developed word ladder solver using BFS
✓ Found nodes at specific distances for social network analysis
✓ Calculated tree diameter using two BFS passes
✓ Detected shortest cycles in both directed and undirected graphs
✓ Understood differences between BFS on directed vs undirected graphs
✓ Analyzed performance characteristics: O(V + E) time, O(V) space
✓ Compared BFS vs DFS to understand when to use each algorithm
✓ Built practical applications: social graph service, grid pathfinding, content recommendation
✓ Understood when BFS is optimal (shortest paths) vs when DFS is better (deep exploration)

You now have a deep understanding of how BFS explores graphs level by level, guaranteeing shortest paths in unweighted graphs. This makes BFS perfect for problems requiring minimum steps, level-order processing, or finding nearby solutions. This foundation will serve you well as you tackle more advanced algorithms like Dijkstra’s shortest path for weighted graphs.

💻 Code Samples

All code examples from this chapter are available in the GitHub repository:

View Chapter 23 Code Samples

Clone the repository to run examples:

git clone https://github.com/dalehurley/codewithphp.git
cd codewithphp/code/php-algorithms/chapter-23
php 01-*.php

Next Steps

In the next chapter, we’ll explore Dijkstra’s algorithm, which extends BFS to find shortest paths in weighted graphs where edges have different costs.

23: Breadth-First Search (BFS)

23: Breadth-First Search (BFS) Intermediate

Overview

Prerequisites

What You’ll Build

Objectives

How BFS Works

BFS Visual Step-by-Step Trace

BFS Queue State Visualization

Basic BFS Implementation

Shortest Path in Unweighted Graph

Finding All Shortest Paths

Bidirectional BFS

Bipartite Graph Detection

Kahn’s Algorithm (BFS-based Topological Sort)

0-1 BFS

Multi-Source BFS

BFS on 2D Grid

Finding Nodes at Distance K

BFS for Tree Diameter

Shortest Cycle Detection

BFS on Directed vs Undirected Graphs

Word Ladder Problem

Complexity Analysis

BFS vs DFS Comparison

Framework Integration Examples

Laravel Graph Service with BFS

Symfony Content Recommendation System

Practical Applications

1. Social Network Friend Suggestions

2. Shortest Route in City Map

Best Practices

Practice Exercises

Exercise 1: Shortest Bridge

Exercise 2: Rotting Oranges

Exercise 3: Binary Tree Level Order Traversal

Exercise 4: Open the Lock

Exercise 5: Word Ladder II

Troubleshooting

Error: “Queue grows too large, memory exhausted”

Problem: BFS finds path but it’s not the shortest

Problem: Infinite loop in BFS

Problem: Wrong path reconstruction

Problem: BFS too slow for large graphs

Problem: Multi-source BFS gives wrong distances

Problem: Grid BFS out of bounds errors

Key Takeaways

Wrap-up

Further Reading

💻 Code Samples

Next Steps