05: Bubble Sort & Selection Sort

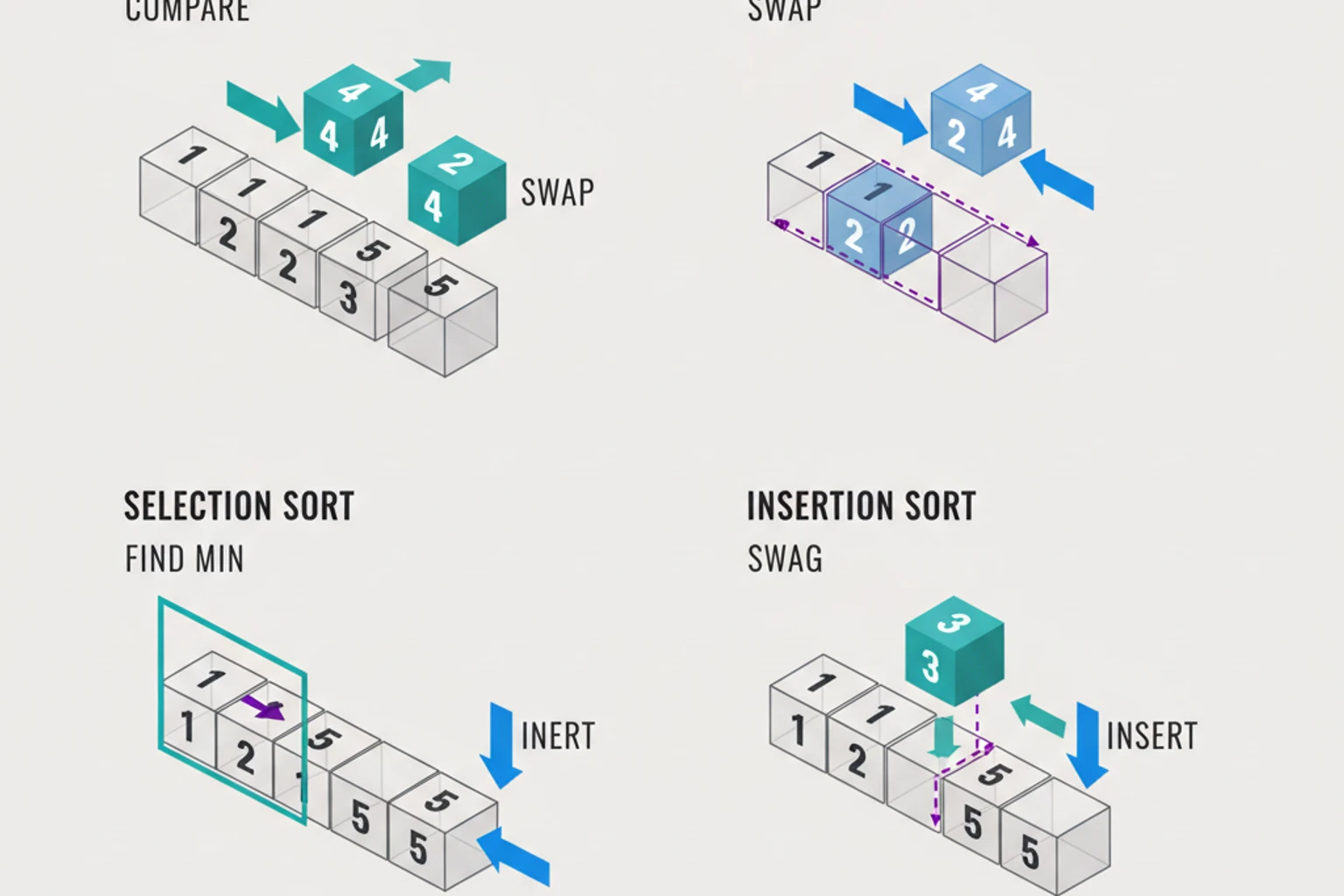
Bubble Sort & Selection Sort Intermediate

Overview

Now that we understand algorithm complexity and how to benchmark performance, let’s dive into our first sorting algorithms. We’ll start with two simple but inefficient sorting algorithms: Bubble Sort and Selection Sort.

While these algorithms aren’t practical for large datasets, they’re excellent learning tools that introduce fundamental sorting concepts. You’ll implement these algorithms from scratch, understand why they’re O(n²), and learn optimization techniques that can dramatically improve performance on certain types of data.

By the end of this chapter, you’ll not only understand how sorting works at a fundamental level, but you’ll also appreciate why modern sorting algorithms are necessary for real-world applications. You’ll benchmark these algorithms against various dataset sizes and patterns, validating theoretical complexity analysis with real measurements.

This hands-on experience will prepare you for more advanced sorting algorithms in upcoming chapters, where you’ll see how clever techniques can reduce O(n²) complexity to O(n log n) or even O(n) in special cases.

What You’ll Learn

Estimated time: 55 minutes

By the end of this chapter, you will:

Implement Bubble Sort and Selection Sort from scratch in PHP
Understand O(n²) time complexity and why it matters for sorting
Learn optimization techniques like early termination for nearly-sorted data
Benchmark these algorithms against various dataset sizes to validate complexity analysis
Recognize when simple sorting algorithms are appropriate vs when to use advanced alternatives

Prerequisites

Before starting this chapter, you should have:

✓ Understanding of Big O notation (60 mins from Chapter 01 if not done)
✓ Familiarity with arrays and loops (10 mins review if needed)
✓ Completion of Chapter 00, Chapter 01, and Chapter 02 (180 mins if not done)
Estimated Time: ~55-65 minutes

What You’ll Build

By the end of this chapter, you will have created:

✅ Complete Bubble Sort implementation with basic and optimized versions
✅ Selection Sort implementation with visualization capabilities
✅ Performance benchmark suite comparing algorithms across different data patterns
✅ Advanced variations including Cocktail Shaker Sort and Comb Sort
✅ Real-world examples sorting user data and finding top K elements
✅ Comprehensive test suite validating algorithm correctness and complexity

Quick Checklist

Complete these hands-on tasks as you work through the chapter:

Implement basic Bubble Sort with nested loops
Add optimization flag to detect if array is already sorted (early termination)
Implement Selection Sort by finding minimum element in each pass
Benchmark both algorithms with different array sizes (100, 500, 1000 items)
Compare performance: random, sorted, and reverse-sorted arrays
(Optional) Implement bidirectional Bubble Sort (Cocktail Shaker Sort)

Why Learn “Slow” Algorithms?

You might wonder: “Why learn algorithms that are inefficient?”

Here’s why:

Foundation: They teach core sorting concepts used in advanced algorithms
Interviews: Simple algorithms are common in technical interviews
Small datasets: They’re perfectly fine for tiny arrays (< 100 items)
Understanding: You’ll appreciate faster algorithms more after seeing slow ones
Comparison: They serve as benchmarks for better algorithms

Bubble Sort

Bubble Sort repeatedly steps through the array, compares adjacent elements, and swaps them if they’re in the wrong order. Larger values “bubble up” to the end.

How It Works

Imagine sorting [5, 2, 8, 1, 9]:

Pass 1:

Compare 5 and 2 → swap → [2, 5, 8, 1, 9]
Compare 5 and 8 → no swap → [2, 5, 8, 1, 9]
Compare 8 and 1 → swap → [2, 5, 1, 8, 9]
Compare 8 and 9 → no swap → [2, 5, 1, 8, 9]
✅ Largest element (9) is now in place

Pass 2:

Compare 2 and 5 → no swap
Compare 5 and 1 → swap → [2, 1, 5, 8, 9]
Compare 5 and 8 → no swap
✅ Second largest (8) is in place

Continue until the array is sorted.

Basic Implementation

<?php

declare(strict_types=1);

function bubbleSort(array $arr): array
{
    $n = count($arr);

    // Outer loop: number of passes
    for ($i = 0; $i < $n - 1; $i++) {
        // Inner loop: comparisons in this pass
        for ($j = 0; $j < $n - $i - 1; $j++) {
            // If current element is greater than next, swap them
            if ($arr[$j] > $arr[$j + 1]) {
                // Swap using array destructuring
                [$arr[$j], $arr[$j + 1]] = [$arr[$j + 1], $arr[$j]];
            }
        }
    }

    return $arr;
}

// Test it
$numbers = [64, 34, 25, 12, 22, 11, 90];
print_r(bubbleSort($numbers));
// Output: Array ( [0] => 11 [1] => 12 [2] => 22 [3] => 25 [4] => 34 [5] => 64 [6] => 90 )

Complexity Analysis

Time Complexity:
- Best case: O(n) - already sorted, with optimization
- Average case: O(n²) - random order
- Worst case: O(n²) - reverse sorted
Space Complexity: O(1) - sorts in place

::: info Why O(n²)? The nested loop structure creates quadratic complexity:

Outer loop runs n-1 times
Inner loop runs (n-1), (n-2), (n-3), …, 1 times
Total comparisons: (n-1) + (n-2) + … + 1 = n(n-1)/2 ≈ n²/2 → O(n²) :::

Optimized Bubble Sort

We can optimize by stopping early if no swaps occur (array is sorted):

<?php

declare(strict_types=1);

function bubbleSortOptimized(array $arr): array
{
    $n = count($arr);

    for ($i = 0; $i < $n - 1; $i++) {
        $swapped = false;

        for ($j = 0; $j < $n - $i - 1; $j++) {
            if ($arr[$j] > $arr[$j + 1]) {
                [$arr[$j], $arr[$j + 1]] = [$arr[$j + 1], $arr[$j]];
                $swapped = true;
            }
        }

        // If no swaps occurred, array is sorted
        if (!$swapped) {
            break;
        }
    }

    return $arr;
}

// Best case: already sorted array
$sorted = [1, 2, 3, 4, 5];
bubbleSortOptimized($sorted); // Only one pass needed!

::: tip Optimization Impact This optimization improves best-case complexity to O(n) when the array is already sorted. This makes bubble sort surprisingly efficient for nearly-sorted data! :::

How Bubble Sort Works

Understanding the mechanics of bubble sort:

Outer loop controls the number of passes through the array
Inner loop compares adjacent elements and swaps them if needed
Optimization: The algorithm can exit early if no swaps occur in a pass, indicating the array is sorted
Each pass guarantees that one more element is in its final position (largest values “bubble up” to the end)

Visualizing Bubble Sort

function bubbleSortWithVisualization(array $arr): array
{
    $n = count($arr);
    echo "Starting array: " . implode(', ', $arr) . "\n\n";

    for ($i = 0; $i < $n - 1; $i++) {
        echo "Pass " . ($i + 1) . ":\n";

        for ($j = 0; $j < $n - $i - 1; $j++) {
            if ($arr[$j] > $arr[$j + 1]) {
                echo "  Swap {$arr[$j]} and {$arr[$j + 1]}\n";
                [$arr[$j], $arr[$j + 1]] = [$arr[$j + 1], $arr[$j]];
            }
        }

        echo "  Result: " . implode(', ', $arr) . "\n\n";
    }

    return $arr;
}

bubbleSortWithVisualization([5, 2, 8, 1, 9]);

Output:

Starting array: 5, 2, 8, 1, 9

Pass 1:
  Swap 5 and 2
  Swap 8 and 1
  Result: 2, 5, 1, 8, 9

Pass 2:
  Swap 5 and 1
  Result: 2, 1, 5, 8, 9

Pass 3:
  Swap 2 and 1
  Result: 1, 2, 5, 8, 9

Pass 4:
  Result: 1, 2, 5, 8, 9

Selection Sort

Selection Sort works by repeatedly finding the minimum element and placing it at the beginning of the unsorted portion.

How It Works

Sorting [64, 25, 12, 22, 11]:

Pass 1:

Find minimum in [64, 25, 12, 22, 11] → 11
Swap with first element → [11, 25, 12, 22, 64]

Pass 2:

Find minimum in [25, 12, 22, 64] → 12
Swap with first unsorted element → [11, 12, 25, 22, 64]

Pass 3:

Find minimum in [25, 22, 64] → 22
Swap → [11, 12, 22, 25, 64]

Pass 4:

Find minimum in [25, 64] → 25
Already in place → [11, 12, 22, 25, 64]

Done!

Implementation

<?php

declare(strict_types=1);

function selectionSort(array $arr): array
{
    $n = count($arr);

    // Move boundary of unsorted portion
    for ($i = 0; $i < $n - 1; $i++) {
        // Find minimum element in unsorted portion
        $minIndex = $i;

        for ($j = $i + 1; $j < $n; $j++) {
            if ($arr[$j] < $arr[$minIndex]) {
                $minIndex = $j;
            }
        }

        // Swap found minimum with first element of unsorted portion
        if ($minIndex !== $i) {
            [$arr[$i], $arr[$minIndex]] = [$arr[$minIndex], $arr[$i]];
        }
    }

    return $arr;
}

// Test
$numbers = [64, 25, 12, 22, 11];
print_r(selectionSort($numbers));
// Output: Array ( [0] => 11 [1] => 12 [2] => 22 [3] => 25 [4] => 64 )

Complexity Analysis

Time Complexity:
- Best case: O(n²) - even if sorted
- Average case: O(n²)
- Worst case: O(n²)
Space Complexity: O(1) - sorts in place

::: warning No Optimization Possible Unlike bubble sort, selection sort always performs O(n²) comparisons regardless of input:

Always makes the same number of comparisons
No early exit optimization possible
Comparisons: (n-1) + (n-2) + … + 1 = n(n-1)/2 → O(n²)

However, it minimizes the number of swaps to O(n), making it useful when write operations are expensive. :::

How Selection Sort Works

Understanding the mechanics of selection sort:

Outer loop moves the boundary between the sorted and unsorted portions of the array
Inner loop scans through the unsorted portion to find the minimum element
Only one swap per pass (at most), making it efficient when write operations are expensive
No early termination is possible—the algorithm always performs all comparisons regardless of the initial order

Selection Sort with Visualization

function selectionSortWithVisualization(array $arr): array
{
    $n = count($arr);
    echo "Starting array: " . implode(', ', $arr) . "\n\n";

    for ($i = 0; $i < $n - 1; $i++) {
        $minIndex = $i;

        // Find minimum
        for ($j = $i + 1; $j < $n; $j++) {
            if ($arr[$j] < $arr[$minIndex]) {
                $minIndex = $j;
            }
        }

        // Swap if needed
        if ($minIndex !== $i) {
            echo "Pass " . ($i + 1) . ": ";
            echo "Swap {$arr[$i]} (position $i) with {$arr[$minIndex]} (position $minIndex)\n";
            [$arr[$i], $arr[$minIndex]] = [$arr[$minIndex], $arr[$i]];
            echo "  Result: " . implode(', ', $arr) . "\n\n";
        }
    }

    return $arr;
}

selectionSortWithVisualization([64, 25, 12, 22, 11]);

Comparing Bubble Sort vs Selection Sort

Let’s benchmark them:

require_once 'Benchmark.php'; // From Chapter 2

$bench = new Benchmark();

// Test with different sizes
$sizes = [100, 500, 1000, 2000];

foreach ($sizes as $size) {
    $data = range(1, $size);
    shuffle($data);

    echo "Array size: $size\n";
    $bench->compare([
        'Bubble Sort' => fn($arr) => bubbleSort($arr),
        'Bubble Sort (Optimized)' => fn($arr) => bubbleSortOptimized($arr),
        'Selection Sort' => fn($arr) => selectionSort($arr),
    ], $data, iterations: 10);
    echo "\n";
}

Key Differences

Feature	Bubble Sort	Selection Sort
Comparisons	O(n²)	O(n²)
Swaps	O(n²) worst case	O(n) always
Best case	O(n) with optimization	O(n²) always
Stable?	Yes	No
When to use	Nearly sorted data	Minimize writes

::: info What is Stability? Stability means equal elements maintain their relative order after sorting. This matters when sorting objects by one field while preserving order from a previous sort:

<?php

declare(strict_types=1);

$students = [
    ['name' => 'Alice', 'score' => 85],
    ['name' => 'Bob', 'score' => 90],
    ['name' => 'Charlie', 'score' => 85],
];

// Stable sort: Alice stays before Charlie (both scored 85)
// Unstable sort: Charlie might come before Alice

// This matters when you sort by multiple fields:
// 1. First sort by name (alphabetical)
// 2. Then stable-sort by score
// Result: Same scores appear in alphabetical order

Bubble sort is stable because it only swaps adjacent elements when needed. Selection sort is unstable because it can swap non-adjacent elements, disrupting the original order. :::

Memory Usage Comparison

Both algorithms are in-place, meaning they sort the array without requiring significant extra memory:

Aspect	Bubble Sort	Selection Sort
Space complexity	O(1)	O(1)
Extra variables	2-3 temp vars	2 index vars
Recursion stack	None	None
Memory efficient?	✅ Yes	✅ Yes

::: info Why Memory Matters In-place sorting is crucial for:

Memory-constrained environments (embedded systems, mobile devices)
Large datasets that barely fit in RAM
Real-time systems where memory allocation is expensive
Systems with fragmented memory where large allocations fail

Both bubble and selection sort excel here, unlike merge sort which requires O(n) extra space. :::

<?php

declare(strict_types=1);

// Demonstrate memory efficiency
$largeArray = range(1, 100000);
shuffle($largeArray);

// These sorts modify the array in-place
$memoryBefore = memory_get_usage();
bubbleSort($largeArray); // Or selectionSort()
$memoryAfter = memory_get_usage();

echo "Memory used: " . ($memoryAfter - $memoryBefore) . " bytes\n";
// Output: ~0-100 bytes (just a few temporary variables)

// Compare to merge sort which would need ~800KB for the same array

Practical Applications

::: tip When to Use Built-in sort() For production code, always use PHP’s built-in sort() function instead of implementing your own:

<?php

$numbers = [64, 34, 25, 12, 22, 11, 90];

// ✅ Production: Use built-in (uses optimized C implementation)
sort($numbers); // Typically uses Quicksort or Timsort

// ❌ Don't implement your own unless:
// - Learning/educational purposes
// - Special sorting requirements
// - Custom comparison logic not supported by built-ins

The examples in this chapter are for learning how algorithms work, not for production use! :::

When Bubble Sort Is Okay

<?php

declare(strict_types=1);

// Tiny array - bubble sort is fine
function sortThreeNumbers(int $a, int $b, int $c): array
{
    $arr = [$a, $b, $c];
    return bubbleSort($arr); // Only 3 elements!
}

// Nearly sorted data
$almostSorted = [1, 2, 3, 5, 4, 6, 7, 8];
bubbleSortOptimized($almostSorted); // Very fast with optimization

When Selection Sort Is Okay

// When write operations are expensive (e.g., flash memory, network)
function sortExpensiveWrites(array $arr): array
{
    // Selection sort minimizes swaps
    return selectionSort($arr);
}

// Finding top K elements
function findTopK(array $arr, int $k): array
{
    // Use k passes of selection sort
    $n = count($arr);

    for ($i = 0; $i < min($k, $n); $i++) {
        $maxIndex = $i;

        for ($j = $i + 1; $j < $n; $j++) {
            if ($arr[$j] > $arr[$maxIndex]) {
                $maxIndex = $j;
            }
        }

        if ($maxIndex !== $i) {
            [$arr[$i], $arr[$maxIndex]] = [$arr[$maxIndex], $arr[$i]];
        }
    }

    return array_slice($arr, 0, $k);
}

$scores = [45, 92, 67, 88, 71, 95, 53];
print_r(findTopK($scores, 3)); // [95, 92, 88]

When NOT to Use These Algorithms

::: danger Avoid for Large Datasets Never use Bubble Sort or Selection Sort for:

❌ Arrays larger than 100 elements — O(n²) becomes painfully slow

100 elements: ~10,000 operations
1,000 elements: ~1,000,000 operations
10,000 elements: ~100,000,000 operations (minutes to complete!)

❌ Performance-critical code paths — Use optimized algorithms instead

❌ Production sorting — PHP’s built-in functions are 10-100x faster

❌ Large objects or complex data — Each swap is expensive

❌ Parallel/concurrent sorting — Not parallelizable due to sequential nature

❌ Real-time applications — Unpredictable performance on random data :::

Example of bad usage:

<?php

declare(strict_types=1);

// ❌ BAD: Sorting large database result set
$customers = $database->query("SELECT * FROM customers")->fetchAll();
// 10,000 records

$start = microtime(true);
$sorted = bubbleSort($customers); // Takes 30+ seconds! ⏱️
$time = microtime(true) - $start;
echo "Bubble sort: {$time}s\n"; // 30+ seconds

// ✅ GOOD: Use built-in sort with custom comparator
$start = microtime(true);
usort($customers, fn($a, $b) => $a['name'] <=> $b['name']);
$time = microtime(true) - $start;
echo "PHP usort: {$time}s\n"; // ~0.05 seconds (600x faster!)

Why built-in functions are faster:

Written in C (compiled, not interpreted)
Use optimized algorithms (Quicksort/Timsort hybrid)
Cache-friendly memory access patterns
Decades of performance tuning

When to use bubble/selection sort:

✅ Educational purposes (learning how sorting works)
✅ Tiny arrays (< 10 elements) where simplicity matters
✅ Nearly-sorted data (bubble sort optimized only)
✅ Embedded systems with extreme memory constraints
✅ Technical interviews to demonstrate understanding

Real-World Example: Sorting User Data

class User
{
    public function __construct(
        public string $name,
        public int $age
    ) {}
}

function sortUsersByAge(array $users): array
{
    $n = count($users);

    // Using bubble sort for small user arrays
    for ($i = 0; $i < $n - 1; $i++) {
        for ($j = 0; $j < $n - $i - 1; $j++) {
            if ($users[$j]->age > $users[$j + 1]->age) {
                [$users[$j], $users[$j + 1]] = [$users[$j + 1], $users[$j]];
            }
        }
    }

    return $users;
}

$users = [
    new User('Alice', 30),
    new User('Bob', 25),
    new User('Charlie', 35),
    new User('David', 25),
];

$sorted = sortUsersByAge($users);

foreach ($sorted as $user) {
    echo "{$user->name}: {$user->age}\n";
}

Quick Decision Guide

Choosing the right sorting approach depends on your specific needs and constraints. Here’s a practical guide to help you decide:

For arrays larger than 100 elements or production code: Always use PHP’s built-in sort() or usort() functions. They’re 10-100x faster, written in optimized C code, and battle-tested across millions of applications.

For smaller arrays in learning or interview contexts:

Nearly sorted data? → Use Bubble Sort (optimized) for O(n) best-case performance
Need stability? → Use Bubble Sort to maintain relative order of equal elements
Minimize write operations? → Use Selection Sort for only O(n) swaps
Random data? → Either algorithm works; both are O(n²) anyway

Decision Table Summary

Scenario	Best Choice	Reason
Array > 100 elements	PHP `sort()`	Much faster, optimized
Production code	PHP `sort()` / `usort()`	Reliable, tested, fast
Nearly sorted data	Bubble Sort (optimized)	O(n) best case
Need stability	Bubble Sort	Maintains relative order
Minimize writes	Selection Sort	Only O(n) swaps
Random small array	Either (or built-in)	Both O(n²) anyway
Learning/Teaching	Both	Understand fundamentals
Memory constrained	Either	Both O(1) space

Common Mistakes to Avoid

::: danger Off-by-One Errors One of the most common bugs in sorting algorithms:

<?php

// ❌ Wrong: goes out of bounds
for ($j = 0; $j < $n; $j++) { // Should be $n - 1
    if ($arr[$j] > $arr[$j + 1]) { // $j + 1 can exceed bounds!
        // This will cause: "Undefined array key" error
    }
}

// ✅ Correct: stop before the last element
for ($j = 0; $j < $n - 1; $j++) {
    if ($arr[$j] > $arr[$j + 1]) {
        [$arr[$j], $arr[$j + 1]] = [$arr[$j + 1], $arr[$j]];
    }
}

Always remember: when comparing $arr[$j] with $arr[$j + 1], loop must stop at $n - 1. :::

::: danger Forgetting to Return Arrays in PHP are passed by value, not reference:

<?php

// ❌ Wrong: modifies in place but doesn't return
function bubbleSort(array $arr): void
{
    // ... sorting logic ...
    // Changes are lost! PHP arrays are passed by value
}

// ✅ Correct: return the modified array
function bubbleSort(array $arr): array
{
    // ... sorting logic ...
    return $arr; // Return is required!
}

// Usage
$numbers = [5, 2, 8];
$sorted = bubbleSort($numbers); // Must capture return value

:::

::: tip Modern PHP Swapping Use array destructuring for elegant swaps:

<?php

// Old way (still works)
$temp = $arr[$i];
$arr[$i] = $arr[$j];
$arr[$j] = $temp;

// ✅ Modern PHP way: array destructuring (PHP 7.1+)
[$arr[$i], $arr[$j]] = [$arr[$j], $arr[$i]];

// This is cleaner, more readable, and equally fast

:::

Cocktail Shaker Sort (Bidirectional Bubble Sort)

An optimization of bubble sort that sorts in both directions:

function cocktailSort(array $arr): array
{
    $n = count($arr);
    $swapped = true;
    $start = 0;
    $end = $n - 1;

    while ($swapped) {
        $swapped = false;

        // Forward pass (left to right)
        for ($i = $start; $i < $end; $i++) {
            if ($arr[$i] > $arr[$i + 1]) {
                [$arr[$i], $arr[$i + 1]] = [$arr[$i + 1], $arr[$i]];
                $swapped = true;
            }
        }

        if (!$swapped) break;

        $swapped = false;
        $end--;

        // Backward pass (right to left)
        for ($i = $end; $i > $start; $i--) {
            if ($arr[$i] < $arr[$i - 1]) {
                [$arr[$i], $arr[$i - 1]] = [$arr[$i - 1], $arr[$i]];
                $swapped = true;
            }
        }

        $start++;
    }

    return $arr;
}

// Test
$numbers = [5, 1, 4, 2, 8, 0, 2];
print_r(cocktailSort($numbers));
// Output: [0, 1, 2, 2, 4, 5, 8]

Advantages over regular bubble sort:

Slightly faster on some inputs
Better handles “turtles” (small values at the end)
Still O(n²) worst case but can be faster in practice

Performance Comparison

require_once 'Benchmark.php';

$bench = new Benchmark();

// Test on different data patterns
$patterns = [
    'Random' => function($n) { $arr = range(1, $n); shuffle($arr); return $arr; },
    'Nearly Sorted' => function($n) {
        $arr = range(1, $n);
        // Swap a few elements
        for ($i = 0; $i < $n / 10; $i++) {
            $j = rand(0, $n - 1);
            $k = rand(0, $n - 1);
            [$arr[$j], $arr[$k]] = [$arr[$k], $arr[$j]];
        }
        return $arr;
    },
    'Reversed' => function($n) { return range($n, 1); },
];

foreach ($patterns as $patternName => $generator) {
    echo "\n{$patternName} data (n=100):\n";
    $data = $generator(100);

    $bench->compare([
        'Bubble Sort' => fn($arr) => bubbleSort($arr),
        'Bubble Sort (Optimized)' => fn($arr) => bubbleSortOptimized($arr),
        'Cocktail Sort' => fn($arr) => cocktailSort($arr),
        'Selection Sort' => fn($arr) => selectionSort($arr),
    ], $data, iterations: 100);
}

Adaptive Bubble Sort

Adaptive sort: performs better on partially sorted data.

function adaptiveBubbleSort(array $arr): array
{
    $n = count($arr);
    $swapped = true;
    $passes = 0;

    while ($swapped) {
        $swapped = false;
        $lastSwap = 0;

        for ($i = 0; $i < $n - $passes - 1; $i++) {
            if ($arr[$i] > $arr[$i + 1]) {
                [$arr[$i], $arr[$i + 1]] = [$arr[$i + 1], $arr[$i]];
                $swapped = true;
                $lastSwap = $i;
            }
        }

        // Optimize: elements after last swap are already sorted
        $passes = $n - $lastSwap - 1;

        if (!$swapped) break;
    }

    return $arr;
}

// Best for nearly sorted data
$nearlySorted = [1, 2, 3, 5, 4, 6, 7, 8, 9, 10];
$start = hrtime(true);
adaptiveBubbleSort($nearlySorted);
$time = (hrtime(true) - $start) / 1_000_000;
echo "Time: {$time}ms\n"; // Very fast!

Comb Sort (Improved Bubble Sort)

Uses a gap larger than 1 and shrinks it:

function combSort(array $arr): array
{
    $n = count($arr);
    $gap = $n;
    $shrink = 1.3;
    $swapped = true;

    while ($gap > 1 || $swapped) {
        // Update gap
        $gap = (int)($gap / $shrink);
        if ($gap < 1) $gap = 1;

        $swapped = false;

        // Compare elements with current gap
        for ($i = 0; $i + $gap < $n; $i++) {
            if ($arr[$i] > $arr[$i + $gap]) {
                [$arr[$i], $arr[$i + $gap]] = [$arr[$i + $gap], $arr[$i]];
                $swapped = true;
            }
        }
    }

    return $arr;
}

// Significantly faster than bubble sort on large arrays
$large = range(1, 1000);
shuffle($large);

$start = hrtime(true);
bubbleSort($large);
$bubbleTime = (hrtime(true) - $start) / 1_000_000;

$start = hrtime(true);
combSort($large);
$combTime = (hrtime(true) - $start) / 1_000_000;

echo "Bubble Sort: {$bubbleTime}ms\n";
echo "Comb Sort: {$combTime}ms\n";
echo "Speedup: " . round($bubbleTime / $combTime, 2) . "x\n";

Interview Questions & Answers

Q1: When would you use bubble sort in production?

Answer:

Very small datasets (< 10 elements) where code simplicity matters
Nearly sorted data with optimization enabled
Educational purposes or as a fallback
When memory is extremely limited (in-place, no recursion)
Realistically: Almost never. Use sort() or better algorithms.

Q2: What’s the space complexity and why?

Answer: O(1) space complexity (constant). Both bubble sort and selection sort are in-place algorithms:

Only use a few variables for swapping and loop counters
Don’t create additional arrays proportional to input size
Compare to merge sort which needs O(n) extra space

Q3: How do you detect if an array is already sorted efficiently?

Answer:

function isSorted(array $arr): bool
{
    $n = count($arr);
    for ($i = 0; $i < $n - 1; $i++) {
        if ($arr[$i] > $arr[$i + 1]) {
            return false;
        }
    }
    return true;
}

// Or using optimized bubble sort:
function isSortedViaBubble(array $arr): bool
{
    $n = count($arr);
    $swapped = false;

    for ($i = 0; $i < $n - 1; $i++) {
        if ($arr[$i] > $arr[$i + 1]) {
            return false; // Early exit on first inversion
        }
    }

    return true; // No swaps needed
}

Q4: Implement stable selection sort

Answer: Regular selection sort is unstable. Make it stable by shifting instead of swapping:

function stableSelectionSort(array $arr): array
{
    $n = count($arr);

    for ($i = 0; $i < $n - 1; $i++) {
        $minIndex = $i;

        // Find minimum
        for ($j = $i + 1; $j < $n; $j++) {
            if ($arr[$j] < $arr[$minIndex]) {
                $minIndex = $j;
            }
        }

        // Instead of swapping, shift elements
        if ($minIndex !== $i) {
            $minValue = $arr[$minIndex];

            // Shift elements right
            for ($j = $minIndex; $j > $i; $j--) {
                $arr[$j] = $arr[$j - 1];
            }

            $arr[$i] = $minValue;
        }
    }

    return $arr;
}

// Test stability
$items = [
    ['name' => 'Alice', 'age' => 30],
    ['name' => 'Bob', 'age' => 25],
    ['name' => 'Charlie', 'age' => 30],
];

// Sort by age (stable)
$sorted = stableSelectionSort($items);
// Alice should still come before Charlie (both age 30)

Q5: Optimize bubble sort for a linked list

Answer:

class ListNode
{
    public function __construct(
        public int $value,
        public ?ListNode $next = null
    ) {}
}

function bubbleSortLinkedList(?ListNode $head): ?ListNode
{
    if ($head === null) return null;

    $swapped = true;

    while ($swapped) {
        $swapped = false;
        $current = $head;

        while ($current->next !== null) {
            if ($current->value > $current->next->value) {
                // Swap values (easier than rewiring pointers)
                $temp = $current->value;
                $current->value = $current->next->value;
                $current->next->value = $temp;
                $swapped = true;
            }

            $current = $current->next;
        }
    }

    return $head;
}

// Create list: 4 -> 2 -> 1 -> 3
$head = new ListNode(4, new ListNode(2, new ListNode(1, new ListNode(3))));
$sorted = bubbleSortLinkedList($head);

// Print: 1 -> 2 -> 3 -> 4
$current = $sorted;
while ($current !== null) {
    echo $current->value . " ";
    $current = $current->next;
}

Q6: Count minimum swaps needed to sort array

Answer:

function minSwapsToSort(array $arr): int
{
    $n = count($arr);
    $arrPos = [];

    // Store value => position
    for ($i = 0; $i < $n; $i++) {
        $arrPos[] = [$arr[$i], $i];
    }

    // Sort by value
    usort($arrPos, fn($a, $b) => $a[0] <=> $b[0]);

    $visited = array_fill(0, $n, false);
    $swaps = 0;

    for ($i = 0; $i < $n; $i++) {
        // Skip if already visited or in correct position
        if ($visited[$i] || $arrPos[$i][1] === $i) {
            continue;
        }

        // Count cycle size
        $cycleSize = 0;
        $j = $i;

        while (!$visited[$j]) {
            $visited[$j] = true;
            $j = $arrPos[$j][1];
            $cycleSize++;
        }

        // Add cycle size - 1 swaps
        if ($cycleSize > 0) {
            $swaps += $cycleSize - 1;
        }
    }

    return $swaps;
}

echo minSwapsToSort([4, 3, 2, 1]); // 2
echo minSwapsToSort([1, 5, 4, 3, 2]); // 2

Comprehensive Benchmark Suite

class SortingBenchmark
{
    private Benchmark $bench;
    private array $results = [];

    public function __construct()
    {
        $this->bench = new Benchmark();
    }

    public function runComprehensiveTests(): void
    {
        $sizes = [10, 50, 100, 500, 1000];
        $dataTypes = [
            'Random' => fn($n) => $this->generateRandom($n),
            'Sorted' => fn($n) => range(1, $n),
            'Reversed' => fn($n) => range($n, 1),
            'Nearly Sorted' => fn($n) => $this->generateNearlySorted($n),
            'Many Duplicates' => fn($n) => $this->generateDuplicates($n),
        ];

        foreach ($sizes as $size) {
            echo "\n" . str_repeat('=', 60) . "\n";
            echo "Array Size: {$size}\n";
            echo str_repeat('=', 60) . "\n";

            foreach ($dataTypes as $typeName => $generator) {
                echo "\n{$typeName}:\n";
                $data = $generator($size);

                $this->bench->compare([
                    'Bubble' => fn($arr) => bubbleSort($arr),
                    'Bubble Optimized' => fn($arr) => bubbleSortOptimized($arr),
                    'Cocktail' => fn($arr) => cocktailSort($arr),
                    'Selection' => fn($arr) => selectionSort($arr),
                    'Comb' => fn($arr) => combSort($arr),
                    'PHP sort()' => function($arr) {
                        sort($arr);
                        return $arr;
                    },
                ], $data, iterations: $size > 500 ? 10 : 100);
            }
        }
    }

    private function generateRandom(int $n): array
    {
        $arr = range(1, $n);
        shuffle($arr);
        return $arr;
    }

    private function generateNearlySorted(int $n): array
    {
        $arr = range(1, $n);
        $swaps = max(1, (int)($n / 10));

        for ($i = 0; $i < $swaps; $i++) {
            $j = rand(0, $n - 1);
            $k = rand(0, $n - 1);
            [$arr[$j], $arr[$k]] = [$arr[$k], $arr[$j]];
        }

        return $arr;
    }

    private function generateDuplicates(int $n): array
    {
        $arr = [];
        $uniqueValues = max(1, (int)($n / 5));

        for ($i = 0; $i < $n; $i++) {
            $arr[] = rand(1, $uniqueValues);
        }

        return $arr;
    }
}

// Run comprehensive benchmarks
$benchmark = new SortingBenchmark();
$benchmark->runComprehensiveTests();

Practice Exercises

Test your understanding with these hands-on challenges:

Exercise 1: Descending Bubble Sort

Goal: Modify bubble sort to sort in descending order instead of ascending.

Requirements:

Create a function bubbleSortDesc() that sorts from largest to smallest
Use the same optimization technique (early termination)
Test with the array [5, 2, 8, 1, 9]

Validation:

<?php

declare(strict_types=1);

function bubbleSortDesc(array $arr): array
{
    // Your code here
}

// Test
$result = bubbleSortDesc([5, 2, 8, 1, 9]);
echo implode(', ', $result);

Expected output:

9, 8, 5, 2, 1

💡 Click to see solution

<?php

declare(strict_types=1);

function bubbleSortDesc(array $arr): array
{
    $n = count($arr);

    for ($i = 0; $i < $n - 1; $i++) {
        $swapped = false;

        for ($j = 0; $j < $n - $i - 1; $j++) {
            // Change > to < for descending order
            if ($arr[$j] < $arr[$j + 1]) {
                [$arr[$j], $arr[$j + 1]] = [$arr[$j + 1], $arr[$j]];
                $swapped = true;
            }
        }

        if (!$swapped) break;
    }

    return $arr;
}

// Test
$result = bubbleSortDesc([5, 2, 8, 1, 9]);
echo implode(', ', $result); // Output: 9, 8, 5, 2, 1

Key insight: Simply flip the comparison operator from > to < to reverse the sort order.

Exercise 2: Count Swaps

Goal: Modify bubble sort to track and return the number of swaps performed.

Requirements:

Return both the sorted array and swap count
Test with random, sorted, and reverse-sorted arrays
Compare swap counts between the three cases

Validation:

<?php

declare(strict_types=1);

function bubbleSortCountSwaps(array $arr): array
{
    $swaps = 0;
    // Your code here
    return ['array' => $arr, 'swaps' => $swaps];
}

// Test
$result = bubbleSortCountSwaps([5, 2, 8, 1, 9]);
echo "Sorted: " . implode(', ', $result['array']) . "\n";
echo "Swaps performed: {$result['swaps']}\n";

Expected output:

Sorted: 1, 2, 5, 8, 9
Swaps performed: 6

💡 Click to see solution

<?php

declare(strict_types=1);

function bubbleSortCountSwaps(array $arr): array
{
    $n = count($arr);
    $swaps = 0;

    for ($i = 0; $i < $n - 1; $i++) {
        for ($j = 0; $j < $n - $i - 1; $j++) {
            if ($arr[$j] > $arr[$j + 1]) {
                [$arr[$j], $arr[$j + 1]] = [$arr[$j + 1], $arr[$j]];
                $swaps++; // Increment counter
            }
        }
    }

    return ['array' => $arr, 'swaps' => $swaps];
}

// Test different patterns
$patterns = [
    'Random' => [5, 2, 8, 1, 9],
    'Sorted' => [1, 2, 5, 8, 9],
    'Reversed' => [9, 8, 5, 2, 1],
];

foreach ($patterns as $name => $data) {
    $result = bubbleSortCountSwaps($data);
    echo "{$name}: {$result['swaps']} swaps\n";
}
// Output:
// Random: 6 swaps
// Sorted: 0 swaps
// Reversed: 10 swaps

Key insight: Reverse-sorted arrays require the maximum number of swaps (n(n-1)/2), while sorted arrays require zero.

Exercise 3: Find Kth Smallest Element

Goal: Use selection sort to efficiently find the Kth smallest element without fully sorting the array.

Requirements:

Only perform K passes of selection sort (not full sort)
Return the Kth smallest element
Must work for K from 1 to n

Validation:

<?php

declare(strict_types=1);

function findKthSmallest(array $arr, int $k): int
{
    // Hint: You only need k passes of selection sort
    // Your code here
}

// Test
echo findKthSmallest([7, 10, 4, 3, 20, 15], 3); // Should output: 7
echo "\n";
echo findKthSmallest([7, 10, 4, 3, 20, 15], 1); // Should output: 3

Expected output:

7
3

💡 Click to see solution

<?php

declare(strict_types=1);

function findKthSmallest(array $arr, int $k): int
{
    $n = count($arr);

    // Only do k passes instead of n-1
    for ($i = 0; $i < $k; $i++) {
        $minIndex = $i;

        // Find minimum in remaining portion
        for ($j = $i + 1; $j < $n; $j++) {
            if ($arr[$j] < $arr[$minIndex]) {
                $minIndex = $j;
            }
        }

        // Swap if needed
        if ($minIndex !== $i) {
            [$arr[$i], $arr[$minIndex]] = [$arr[$minIndex], $arr[$i]];
        }
    }

    // After k passes, kth smallest is at position k-1
    return $arr[$k - 1];
}

// Test
echo findKthSmallest([7, 10, 4, 3, 20, 15], 3); // Output: 7
echo "\n";
echo findKthSmallest([7, 10, 4, 3, 20, 15], 1); // Output: 3
echo "\n";

// After 3 passes: [3, 4, 7, 10, 20, 15]
//                      ^
//                   3rd smallest

Key insight: This optimization reduces time complexity from O(n²) to O(k×n), which is much faster when k << n.

Key Takeaways

Bubble Sort: Simple but O(n²), good for nearly sorted data with optimization
Selection Sort: Always O(n²), but minimizes swaps
Both are in-place algorithms (O(1) space)
Bubble sort is stable, selection sort is not
Use only for small datasets (< 100 elements)
Understanding these helps you appreciate better algorithms

Wrap-up

Congratulations! You’ve completed Chapter 05. Here’s what you accomplished:

✅ Implemented Bubble Sort from scratch with both basic and optimized versions
✅ Mastered Selection Sort and understood its unique characteristics
✅ Analyzed time complexity of O(n²) algorithms with mathematical proofs
✅ Created visualization functions to see how sorting works step-by-step
✅ Built benchmark suites comparing algorithms across different data patterns
✅ Explored advanced variations like Cocktail Shaker Sort and Comb Sort
✅ Understood stability in sorting and why it matters
✅ Learned when to use simple algorithms vs advanced alternatives
✅ Applied sorting concepts to real-world problems like finding top K elements

You now have a solid foundation in sorting algorithms and understand the fundamental trade-offs between simplicity and efficiency. This knowledge will make the more advanced sorting algorithms in the next chapters much easier to understand.

::: tip What You Can Do Now

Sort small arrays efficiently with appropriate algorithms
Optimize bubble sort for nearly-sorted data
Choose between bubble sort and selection sort based on constraints
Benchmark and compare algorithm performance empirically
Explain time complexity with both theory and practical examples :::

What’s Next: Leveling Up to O(n log n)

You’ve mastered O(n²) sorting algorithms—congratulations! But there’s a dramatic performance leap waiting in the next chapter.

Bridge to Chapter 06: Better Algorithms

Here’s what changes when we move beyond O(n²):

This Chapter (05)	Next Chapter (06)	Improvement
Bubble Sort: O(n²)	Insertion Sort: O(n²) but adaptive	⚡ 10x faster on nearly-sorted data
Selection Sort: Always O(n²)	Merge Sort: Always O(n log n)	🚀 100x faster on 10,000 elements
Simple nested loops	Divide-and-conquer strategy	🧠 Powerful new paradigm
Good for learning	Good for production	💼 Real-world applicable
10,000 elements: 100M ops	10,000 elements: 130K ops	⚡ 770x improvement!

The key difference: O(n log n) algorithms like Merge Sort use recursion and divide-and-conquer—they split problems into smaller subproblems, solve them independently, and combine results. This strategy reduces 100 million operations to just 130,000!

What You’ll Learn Next

In Chapter 06: Insertion Sort & Merge Sort, you’ll:

Insertion Sort — Your first adaptive algorithm (speeds up on nearly-sorted data)
Merge Sort — Your first O(n log n) algorithm (reliably fast on any data)
Divide-and-conquer — A paradigm you’ll use throughout the series
Stable sorting — Why maintaining order matters for real applications
Recursive thinking — Breaking problems down to solve them efficiently

Why this matters: The jump from O(n²) to O(n log n) is one of the most important leaps in algorithm performance. Once you understand it, you’ll never look at nested loops the same way!

Ready to level up? → Continue to Chapter 06: Insertion Sort & Merge Sort

💻 Code Samples

All code examples from this chapter are available in the GitHub repository:

View Chapter 05 Code Samples

Files included:

01-sorting-algorithms.php - Complete sorting implementations including Bubble Sort (basic and optimized), Selection Sort, Cocktail Shaker Sort, visualizations, and performance benchmarks
README.md - Complete documentation and usage guide

Clone the repository to run the examples locally:

git clone https://github.com/dalehurley/codewithphp.git
cd codewithphp/code/php-algorithms/chapter-05
php 01-sorting-algorithms.php

Continue to Chapter 06: Insertion Sort & Merge Sort.

05: Bubble Sort & Selection Sort

Bubble Sort & Selection Sort Intermediate

Overview

What You’ll Learn

Prerequisites

What You’ll Build

Quick Checklist

Why Learn “Slow” Algorithms?

Bubble Sort

How It Works

Basic Implementation

Complexity Analysis

Optimized Bubble Sort

How Bubble Sort Works

Visualizing Bubble Sort

Selection Sort

How It Works

Implementation

Complexity Analysis

How Selection Sort Works

Selection Sort with Visualization

Comparing Bubble Sort vs Selection Sort

Key Differences

Memory Usage Comparison

Practical Applications

When Bubble Sort Is Okay

When Selection Sort Is Okay

When NOT to Use These Algorithms

Real-World Example: Sorting User Data

Quick Decision Guide

Decision Table Summary

Common Mistakes to Avoid

Cocktail Shaker Sort (Bidirectional Bubble Sort)

Performance Comparison

Adaptive Bubble Sort

Comb Sort (Improved Bubble Sort)

Interview Questions & Answers

Q1: When would you use bubble sort in production?

Q2: What’s the space complexity and why?

Q3: How do you detect if an array is already sorted efficiently?

Q4: Implement stable selection sort

Q5: Optimize bubble sort for a linked list

Q6: Count minimum swaps needed to sort array

Comprehensive Benchmark Suite

Practice Exercises

Exercise 1: Descending Bubble Sort

Exercise 2: Count Swaps

Exercise 3: Find Kth Smallest Element

Key Takeaways

Wrap-up

Further Reading

What’s Next: Leveling Up to O(n log n)

Bridge to Chapter 06: Better Algorithms

What You’ll Learn Next

💻 Code Samples