Home›Series›PHP Algorithms›Chapter 19

19: Tree Traversal Algorithms Intermediate

What You'll Learn

• Master in-order, pre-order, and post-order depth-first traversals
• Implement level-order (breadth-first) traversal with queues
• Build both recursive and iterative versions of each traversal
• Apply traversals to solve practical tree problems
• Understand when to use each traversal strategy

Estimated Time: ~50 minutes

Prerequisites

Before starting this chapter, you should have:

• ✓ Strong understanding of binary search trees from Chapter 18
• ✓ Familiarity with recursion from Chapter 3
• ✓ Knowledge of stacks and queues from Chapter 17
• ✓ Completion of Chapters 15-18

Overview

Tree traversal is the process of visiting each node in a tree data structure exactly once in a systematic way. Think of it as taking different "tours" through your tree—each traversal strategy visits the same nodes but in a different order, making each one useful for different problems.

In this chapter, you'll master the four fundamental traversal algorithms: in-order, pre-order, post-order (all depth-first), and level-order (breadth-first). You'll implement each traversal both recursively and iteratively, understand their time and space complexities, and apply them to solve practical problems like expression tree evaluation, tree serialization, and path finding.

Understanding traversal algorithms is fundamental to working with trees and forms the basis for many advanced tree-based algorithms. Whether you're processing file systems, evaluating expressions, or navigating DOM structures, traversal algorithms provide the systematic approach you need.

What You'll Build

By the end of this chapter, you will have created:

• Complete implementations of all four traversal types (in-order, pre-order, post-order, level-order)
• Both recursive and iterative versions of each traversal algorithm
• Reverse traversals for descending order output
• Iterator pattern implementation making trees iterable with foreach
• Generator-based traversals for memory-efficient processing
• Morris traversal implementation for O(1) space complexity
• Expression tree evaluator using post-order traversal
• Tree serialization/deserialization system using pre-order and level-order traversals
• Path finding algorithms for tree structures
• Advanced variations: vertical order, boundary traversal, and tree views
• Practical applications: file system traversal and DOM tree processing

Understanding Tree Traversal

Tree traversal algorithms differ from linear data structure traversal because trees are hierarchical. We need strategies to visit nodes in a specific order.

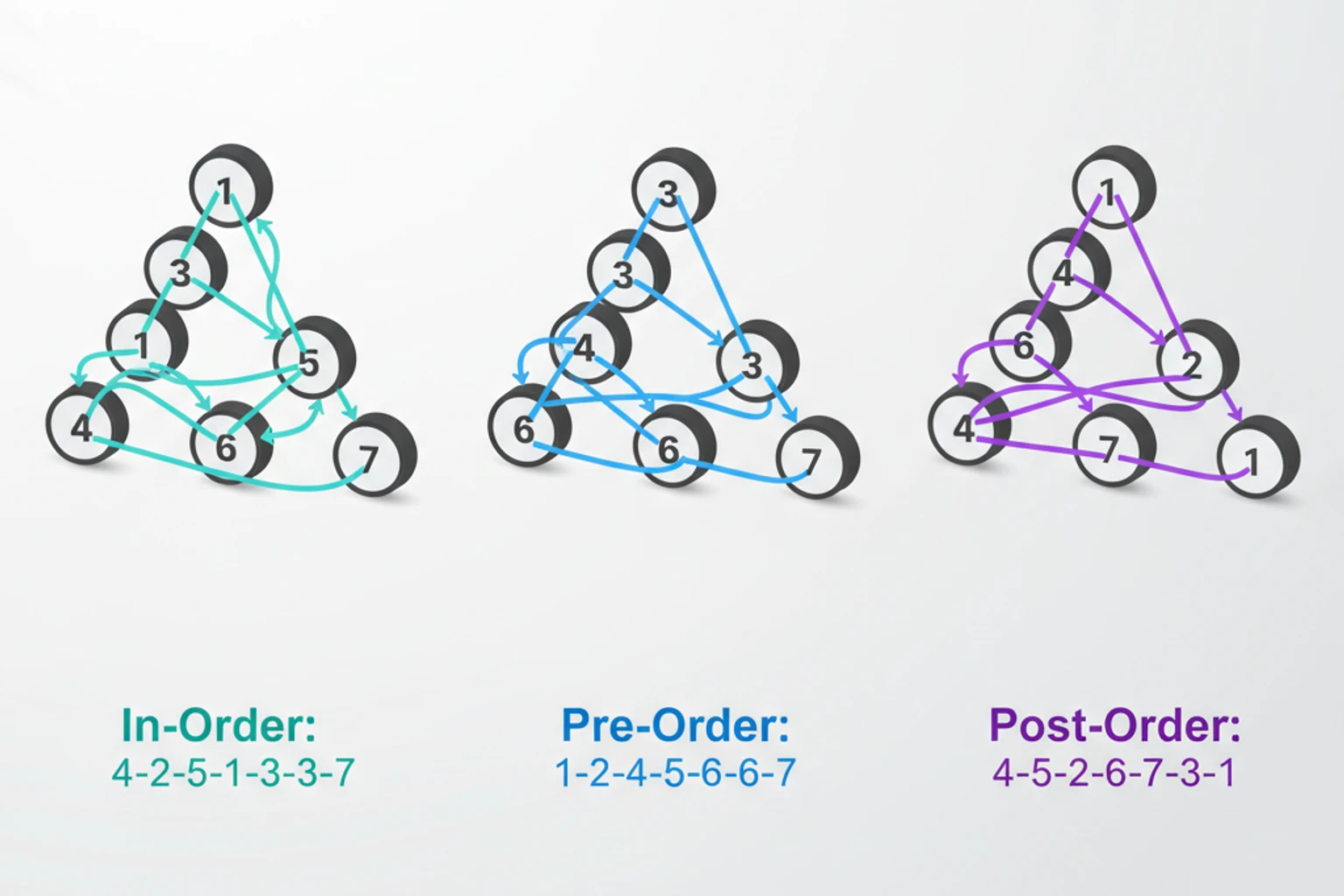
Visual Example

Consider this binary tree:

        4
       / \
      2   6
     / \ / \
    1  3 5  7

Different traversal orders produce different sequences:

• In-order: 1 → 2 → 3 → 4 → 5 → 6 → 7 (sorted for BST)
• Pre-order: 4 → 2 → 1 → 3 → 6 → 5 → 7 (root first)
• Post-order: 1 → 3 → 2 → 5 → 7 → 6 → 4 (root last)
• Level-order: 4 → 2 → 6 → 1 → 3 → 5 → 7 (level by level)

Key Concepts

• Visiting: Processing a node (reading data, printing, modifying)
• Traversing: Moving through the tree systematically
• Depth-First: Explore as far as possible along each branch before backtracking
• Breadth-First: Explore all nodes at the current depth before moving deeper

Depth-First Traversals

Depth-first traversals use a stack (either explicitly or via recursion) to explore branches deeply before backtracking.

In-Order Traversal (Left-Root-Right)

In-order traversal visits the left subtree, then the root, then the right subtree. For BSTs, this produces sorted output in ascending order, making it perfect for retrieving elements in sorted sequence.

Order: Left → Root → Right

Use Cases:

• Getting sorted output from a BST
• Expression tree evaluation (infix notation)
• Binary tree validation

# filename: tree-traversal.php
<?php

declare(strict_types=1);

class TreeNode
{
    public function __construct(
        public mixed $data,
        public ?TreeNode $left = null,
        public ?TreeNode $right = null
    ) {}
}

class TreeTraversal
{
    // Recursive in-order traversal
    public function inOrderRecursive(?TreeNode $node, array &$result = []): array
    {
        if ($node === null) {
            return $result;
        }

        $this->inOrderRecursive($node->left, $result);  // Left
        $result[] = $node->data;                         // Root
        $this->inOrderRecursive($node->right, $result);  // Right

        return $result;
    }

    // Iterative in-order traversal using explicit stack
    public function inOrderIterative(?TreeNode $root): array
    {
        $result = [];
        $stack = [];
        $current = $root;

        while ($current !== null || !empty($stack)) {
            // Go to the leftmost node
            while ($current !== null) {
                $stack[] = $current;
                $current = $current->left;
            }

            // Current is null, so we backtrack
            $current = array_pop($stack);
            $result[] = $current->data;

            // Visit the right subtree
            $current = $current->right;
        }

        return $result;
    }
}

// Example usage
$tree = new TreeNode(4,
    new TreeNode(2,
        new TreeNode(1),
        new TreeNode(3)
    ),
    new TreeNode(6,
        new TreeNode(5),
        new TreeNode(7)
    )
);

$traversal = new TreeTraversal();
print_r($traversal->inOrderRecursive($tree));    // [1, 2, 3, 4, 5, 6, 7]
print_r($traversal->inOrderIterative($tree));    // [1, 2, 3, 4, 5, 6, 7]

Pre-Order Traversal (Root-Left-Right)

Pre-order traversal visits the root first, then the left subtree, then the right subtree. This order is useful for creating a copy of the tree, serialization, or generating prefix expressions.

Order: Root → Left → Right

Use Cases:

• Tree serialization (saving tree structure)
• Creating a copy of the tree
• Prefix expression generation
• Directory structure printing

# filename: pre-order-traversal.php
<?php

declare(strict_types=1);

class TreeTraversal
{
    // Recursive pre-order traversal
    public function preOrderRecursive(?TreeNode $node, array &$result = []): array
    {
        if ($node === null) {
            return $result;
        }

        $result[] = $node->data;                          // Root
        $this->preOrderRecursive($node->left, $result);   // Left
        $this->preOrderRecursive($node->right, $result);  // Right

        return $result;
    }

    // Iterative pre-order traversal
    public function preOrderIterative(?TreeNode $root): array
    {
        if ($root === null) {
            return [];
        }

        $result = [];
        $stack = [$root];

        while (!empty($stack)) {
            $node = array_pop($stack);
            $result[] = $node->data;

            // Push right first so left is processed first (LIFO)
            if ($node->right !== null) {
                $stack[] = $node->right;
            }
            if ($node->left !== null) {
                $stack[] = $node->left;
            }
        }

        return $result;
    }
}

// Example
$tree = new TreeNode(4,
    new TreeNode(2,
        new TreeNode(1),
        new TreeNode(3)
    ),
    new TreeNode(6,
        new TreeNode(5),
        new TreeNode(7)
    )
);

$traversal = new TreeTraversal();
print_r($traversal->preOrderRecursive($tree));   // [4, 2, 1, 3, 6, 5, 7]
print_r($traversal->preOrderIterative($tree));   // [4, 2, 1, 3, 6, 5, 7]

Post-Order Traversal (Left-Right-Root)

Post-order traversal visits the left subtree, then the right subtree, then the root. This order ensures children are processed before their parent, making it ideal for deletion and postfix expression evaluation.

Order: Left → Right → Root

Use Cases:

• Tree deletion (children before parent)
• Postfix expression evaluation
• Calculating directory sizes
• Expression tree evaluation

# filename: post-order-traversal.php
<?php

declare(strict_types=1);

class TreeTraversal
{
    // Recursive post-order traversal
    public function postOrderRecursive(?TreeNode $node, array &$result = []): array
    {
        if ($node === null) {
            return $result;
        }

        $this->postOrderRecursive($node->left, $result);   // Left
        $this->postOrderRecursive($node->right, $result);  // Right
        $result[] = $node->data;                           // Root

        return $result;
    }

    // Iterative post-order traversal (two-stack approach)
    public function postOrderIterative(?TreeNode $root): array
    {
        if ($root === null) {
            return [];
        }

        $result = [];
        $stack1 = [$root];
        $stack2 = [];

        // Fill second stack with reverse post-order
        while (!empty($stack1)) {
            $node = array_pop($stack1);
            $stack2[] = $node;

            if ($node->left !== null) {
                $stack1[] = $node->left;
            }
            if ($node->right !== null) {
                $stack1[] = $node->right;
            }
        }

        // Pop from second stack to get post-order
        while (!empty($stack2)) {
            $result[] = array_pop($stack2)->data;
        }

        return $result;
    }

    // Iterative post-order traversal (single-stack approach)
    public function postOrderIterativeSingleStack(?TreeNode $root): array
    {
        if ($root === null) {
            return [];
        }

        $result = [];
        $stack = [];
        $lastVisited = null;
        $current = $root;

        while (!empty($stack) || $current !== null) {
            if ($current !== null) {
                $stack[] = $current;
                $current = $current->left;
            } else {
                $peekNode = end($stack);

                // If right child exists and traversing from left, go right
                if ($peekNode->right !== null && $lastVisited !== $peekNode->right) {
                    $current = $peekNode->right;
                } else {
                    // Visit the node
                    $result[] = $peekNode->data;
                    $lastVisited = array_pop($stack);
                }
            }
        }

        return $result;
    }
}

// Example
$tree = new TreeNode(4,
    new TreeNode(2,
        new TreeNode(1),
        new TreeNode(3)
    ),
    new TreeNode(6,
        new TreeNode(5),
        new TreeNode(7)
    )
);

$traversal = new TreeTraversal();
print_r($traversal->postOrderRecursive($tree));  // [1, 3, 2, 5, 7, 6, 4]
print_r($traversal->postOrderIterative($tree));  // [1, 3, 2, 5, 7, 6, 4]

Breadth-First Traversal

Breadth-first (level-order) traversal visits nodes level by level, from left to right. This approach uses a queue to process nodes at the same depth before moving to the next level.

Use Cases:

• Level-wise processing
• Finding shortest path in unweighted trees
• Printing tree structure level by level
• Binary tree level-order serialization

Level-Order Traversal

# filename: level-order-traversal.php
<?php

declare(strict_types=1);

class TreeTraversal
{
    // Level-order traversal using queue
    public function levelOrder(?TreeNode $root): array
    {
        if ($root === null) {
            return [];
        }

        $result = [];
        $queue = [$root];

        while (!empty($queue)) {
            $node = array_shift($queue);
            $result[] = $node->data;

            if ($node->left !== null) {
                $queue[] = $node->left;
            }
            if ($node->right !== null) {
                $queue[] = $node->right;
            }
        }

        return $result;
    }

    // Level-order traversal grouped by level
    public function levelOrderGrouped(?TreeNode $root): array
    {
        if ($root === null) {
            return [];
        }

        $result = [];
        $queue = [$root];

        while (!empty($queue)) {
            $levelSize = count($queue);
            $currentLevel = [];

            for ($i = 0; $i < $levelSize; $i++) {
                $node = array_shift($queue);
                $currentLevel[] = $node->data;

                if ($node->left !== null) {
                    $queue[] = $node->left;
                }
                if ($node->right !== null) {
                    $queue[] = $node->right;
                }
            }

            $result[] = $currentLevel;
        }

        return $result;
    }

    // Zigzag level-order traversal (alternate left-to-right and right-to-left)
    public function zigzagLevelOrder(?TreeNode $root): array
    {
        if ($root === null) {
            return [];
        }

        $result = [];
        $queue = [$root];
        $leftToRight = true;

        while (!empty($queue)) {
            $levelSize = count($queue);
            $currentLevel = [];

            for ($i = 0; $i < $levelSize; $i++) {
                $node = array_shift($queue);

                if ($leftToRight) {
                    $currentLevel[] = $node->data;
                } else {
                    array_unshift($currentLevel, $node->data);
                }

                if ($node->left !== null) {
                    $queue[] = $node->left;
                }
                if ($node->right !== null) {
                    $queue[] = $node->right;
                }
            }

            $result[] = $currentLevel;
            $leftToRight = !$leftToRight;
        }

        return $result;
    }
}

// Example
$tree = new TreeNode(4,
    new TreeNode(2,
        new TreeNode(1),
        new TreeNode(3)
    ),
    new TreeNode(6,
        new TreeNode(5),
        new TreeNode(7)
    )
);

$traversal = new TreeTraversal();
print_r($traversal->levelOrder($tree));
// [4, 2, 6, 1, 3, 5, 7]

print_r($traversal->levelOrderGrouped($tree));
// [[4], [2, 6], [1, 3, 5, 7]]

print_r($traversal->zigzagLevelOrder($tree));
// [[4], [6, 2], [1, 3, 5, 7]]

Reverse Traversals

Reverse traversals visit nodes in the opposite order of their standard counterparts. The most common is reverse in-order, which produces descending order output from a BST.

Reverse In-Order Traversal (Right-Root-Left)

# filename: reverse-traversal.php
<?php

declare(strict_types=1);

class TreeTraversal
{
    // Reverse in-order: Right → Root → Left (descending order for BST)
    public function reverseInOrder(?TreeNode $node, array &$result = []): array
    {
        if ($node === null) {
            return $result;
        }

        $this->reverseInOrder($node->right, $result);  // Right
        $result[] = $node->data;                        // Root
        $this->reverseInOrder($node->left, $result);   // Left

        return $result;
    }

    // Iterative reverse in-order
    public function reverseInOrderIterative(?TreeNode $root): array
    {
        $result = [];
        $stack = [];
        $current = $root;

        while ($current !== null || !empty($stack)) {
            // Go to the rightmost node
            while ($current !== null) {
                $stack[] = $current;
                $current = $current->right;
            }

            $current = array_pop($stack);
            $result[] = $current->data;
            $current = $current->left;
        }

        return $result;
    }
}

// Example: BST descending order
$tree = new TreeNode(4,
    new TreeNode(2,
        new TreeNode(1),
        new TreeNode(3)
    ),
    new TreeNode(6,
        new TreeNode(5),
        new TreeNode(7)
    )
);

$traversal = new TreeTraversal();
print_r($traversal->reverseInOrder($tree));  // [7, 6, 5, 4, 3, 2, 1] (descending)

Iterator Pattern: Making Trees Iterable

PHP's Iterator interface allows trees to be used with foreach loops, making traversal more intuitive and memory-efficient.

# filename: tree-iterator.php
<?php

declare(strict_types=1);

class TreeIterator implements Iterator
{
    private array $nodes = [];
    private int $position = 0;
    private string $traversalType;

    public function __construct(?TreeNode $root, string $traversalType = 'inorder')
    {
        $this->traversalType = $traversalType;
        $this->buildTraversal($root);
    }

    private function buildTraversal(?TreeNode $node): void
    {
        if ($node === null) {
            return;
        }

        match($this->traversalType) {
            'inorder' => $this->inOrder($node),
            'preorder' => $this->preOrder($node),
            'postorder' => $this->postOrder($node),
            'levelorder' => $this->levelOrder($node),
            default => throw new InvalidArgumentException("Unknown traversal type")
        };
    }

    private function inOrder(?TreeNode $node): void
    {
        if ($node === null) return;
        $this->inOrder($node->left);
        $this->nodes[] = $node->data;
        $this->inOrder($node->right);
    }

    private function preOrder(?TreeNode $node): void
    {
        if ($node === null) return;
        $this->nodes[] = $node->data;
        $this->preOrder($node->left);
        $this->preOrder($node->right);
    }

    private function postOrder(?TreeNode $node): void
    {
        if ($node === null) return;
        $this->postOrder($node->left);
        $this->postOrder($node->right);
        $this->nodes[] = $node->data;
    }

    private function levelOrder(?TreeNode $root): void
    {
        if ($root === null) return;
        $queue = [$root];
        while (!empty($queue)) {
            $node = array_shift($queue);
            $this->nodes[] = $node->data;
            if ($node->left !== null) $queue[] = $node->left;
            if ($node->right !== null) $queue[] = $node->right;
        }
    }

    // Iterator interface methods
    public function current(): mixed
    {
        return $this->nodes[$this->position];
    }

    public function key(): int
    {
        return $this->position;
    }

    public function next(): void
    {
        $this->position++;
    }

    public function rewind(): void
    {
        $this->position = 0;
    }

    public function valid(): bool
    {
        return isset($this->nodes[$this->position]);
    }
}

// Usage
$tree = new TreeNode(4,
    new TreeNode(2, new TreeNode(1), new TreeNode(3)),
    new TreeNode(6, new TreeNode(5), new TreeNode(7))
);

// Iterate with foreach
foreach (new TreeIterator($tree, 'inorder') as $value) {
    echo $value . ' ';  // 1 2 3 4 5 6 7
}

Generator-Based Traversals

PHP generators provide memory-efficient traversal by yielding values one at a time instead of building an entire array.

# filename: generator-traversal.php
<?php

declare(strict_types=1);

class TreeTraversal
{
    // Generator-based in-order traversal (memory efficient)
    public function inOrderGenerator(?TreeNode $node): Generator
    {
        if ($node === null) {
            return;
        }

        yield from $this->inOrderGenerator($node->left);
        yield $node->data;
        yield from $this->inOrderGenerator($node->right);
    }

    // Generator-based level-order traversal
    public function levelOrderGenerator(?TreeNode $root): Generator
    {
        if ($root === null) {
            return;
        }

        $queue = [$root];
        while (!empty($queue)) {
            $node = array_shift($queue);
            yield $node->data;
            if ($node->left !== null) $queue[] = $node->left;
            if ($node->right !== null) $queue[] = $node->right;
        }
    }
}

// Usage: Memory efficient for large trees
$tree = new TreeNode(4,
    new TreeNode(2, new TreeNode(1), new TreeNode(3)),
    new TreeNode(6, new TreeNode(5), new TreeNode(7))
);

$traversal = new TreeTraversal();
foreach ($traversal->inOrderGenerator($tree) as $value) {
    echo $value . ' ';  // Processes one at a time, no array storage
}

Morris Traversal (Space-Optimized)

Morris traversal achieves O(1) space complexity by using threaded binary trees (temporarily modifying tree structure). This advanced technique eliminates the need for an explicit stack or recursion, making it ideal for memory-constrained environments.

Key Concept: The algorithm temporarily creates threads (links) from the rightmost node of a left subtree back to the current node, allowing it to traverse back without using a stack.

Trade-offs:

• ✅ O(1) space complexity
• ✅ O(n) time complexity (same as other traversals)
• ⚠️ Temporarily modifies the tree structure
• ⚠️ More complex to understand and implement

# filename: morris-traversal.php
<?php

declare(strict_types=1);

class TreeTraversal
{
    // Morris in-order traversal (O(1) space)
    public function morrisInOrder(?TreeNode $root): array
    {
        $result = [];
        $current = $root;

        while ($current !== null) {
            if ($current->left === null) {
                // No left child, visit current and go right
                $result[] = $current->data;
                $current = $current->right;
            } else {
                // Find the inorder predecessor
                $predecessor = $current->left;
                while ($predecessor->right !== null && $predecessor->right !== $current) {
                    $predecessor = $predecessor->right;
                }

                if ($predecessor->right === null) {
                    // Create thread (temporary link)
                    $predecessor->right = $current;
                    $current = $current->left;
                } else {
                    // Thread already exists, remove it
                    $predecessor->right = null;
                    $result[] = $current->data;
                    $current = $current->right;
                }
            }
        }

        return $result;
    }

    // Morris pre-order traversal (O(1) space)
    public function morrisPreOrder(?TreeNode $root): array
    {
        $result = [];
        $current = $root;

        while ($current !== null) {
            if ($current->left === null) {
                $result[] = $current->data;
                $current = $current->right;
            } else {
                $predecessor = $current->left;
                while ($predecessor->right !== null && $predecessor->right !== $current) {
                    $predecessor = $predecessor->right;
                }

                if ($predecessor->right === null) {
                    $result[] = $current->data;  // Visit before going left
                    $predecessor->right = $current;
                    $current = $current->left;
                } else {
                    $predecessor->right = null;
                    $current = $current->right;
                }
            }
        }

        return $result;
    }
}

Traversal Applications

1. Expression Tree Evaluation

# filename: expression-tree-evaluator.php
<?php

declare(strict_types=1);

class ExpressionNode extends TreeNode
{
    public function __construct(
        public mixed $data,
        public ?ExpressionNode $left = null,
        public ?ExpressionNode $right = null
    ) {}
}

class ExpressionTreeEvaluator
{
    // Evaluate expression tree using post-order traversal
    public function evaluate(?ExpressionNode $node): float
    {
        if ($node === null) {
            return 0;
        }

        // Leaf node (operand)
        if ($node->left === null && $node->right === null) {
            return (float)$node->data;
        }

        // Evaluate left and right subtrees
        $leftValue = $this->evaluate($node->left);
        $rightValue = $this->evaluate($node->right);

        // Apply operator
        return match($node->data) {
            '+' => $leftValue + $rightValue,
            '-' => $leftValue - $rightValue,
            '*' => $leftValue * $rightValue,
            '/' => $leftValue / $rightValue,
            default => throw new InvalidArgumentException("Unknown operator: {$node->data}")
        };
    }

    // Build infix expression using in-order traversal
    public function toInfix(?ExpressionNode $node): string
    {
        if ($node === null) {
            return '';
        }

        if ($node->left === null && $node->right === null) {
            return (string)$node->data;
        }

        $left = $this->toInfix($node->left);
        $right = $this->toInfix($node->right);

        return "({$left} {$node->data} {$right})";
    }

    // Build prefix expression using pre-order traversal
    public function toPrefix(?ExpressionNode $node): string
    {
        if ($node === null) {
            return '';
        }

        if ($node->left === null && $node->right === null) {
            return (string)$node->data;
        }

        $left = $this->toPrefix($node->left);
        $right = $this->toPrefix($node->right);

        return "{$node->data} {$left} {$right}";
    }

    // Build postfix expression using post-order traversal
    public function toPostfix(?ExpressionNode $node): string
    {
        if ($node === null) {
            return '';
        }

        if ($node->left === null && $node->right === null) {
            return (string)$node->data;
        }

        $left = $this->toPostfix($node->left);
        $right = $this->toPostfix($node->right);

        return "{$left} {$right} {$node->data}";
    }
}

// Example: Expression tree for ((3 + 5) * 2)
$tree = new ExpressionNode('*',
    new ExpressionNode('+',
        new ExpressionNode(3),
        new ExpressionNode(5)
    ),
    new ExpressionNode(2)
);

$evaluator = new ExpressionTreeEvaluator();
echo $evaluator->evaluate($tree);      // 16
echo $evaluator->toInfix($tree);       // ((3 + 5) * 2)
echo $evaluator->toPrefix($tree);      // * + 3 5 2
echo $evaluator->toPostfix($tree);     // 3 5 + 2 *

2. Tree Serialization and Deserialization

# filename: tree-serializer.php
<?php

declare(strict_types=1);

class TreeSerializer
{
    private const NULL_MARKER = '#';

    // Serialize using pre-order traversal
    public function serialize(?TreeNode $root): string
    {
        $result = [];
        $this->serializeHelper($root, $result);
        return implode(',', $result);
    }

    private function serializeHelper(?TreeNode $node, array &$result): void
    {
        if ($node === null) {
            $result[] = self::NULL_MARKER;
            return;
        }

        $result[] = $node->data;
        $this->serializeHelper($node->left, $result);
        $this->serializeHelper($node->right, $result);
    }

    // Deserialize
    public function deserialize(string $data): ?TreeNode
    {
        $values = explode(',', $data);
        $index = 0;
        return $this->deserializeHelper($values, $index);
    }

    private function deserializeHelper(array $values, int &$index): ?TreeNode
    {
        if ($index >= count($values) || $values[$index] === self::NULL_MARKER) {
            $index++;
            return null;
        }

        $node = new TreeNode($values[$index++]);
        $node->left = $this->deserializeHelper($values, $index);
        $node->right = $this->deserializeHelper($values, $index);

        return $node;
    }

    // Serialize using level-order traversal
    public function serializeLevelOrder(?TreeNode $root): string
    {
        if ($root === null) {
            return '';
        }

        $result = [];
        $queue = [$root];

        while (!empty($queue)) {
            $node = array_shift($queue);

            if ($node === null) {
                $result[] = self::NULL_MARKER;
            } else {
                $result[] = $node->data;
                $queue[] = $node->left;
                $queue[] = $node->right;
            }
        }

        return implode(',', $result);
    }
}

// Example
$tree = new TreeNode(1,
    new TreeNode(2),
    new TreeNode(3,
        new TreeNode(4),
        new TreeNode(5)
    )
);

$serializer = new TreeSerializer();
$serialized = $serializer->serialize($tree);
echo $serialized . "\n";  // 1,2,#,#,3,4,#,#,5,#,#

$deserialized = $serializer->deserialize($serialized);
$reserialized = $serializer->serialize($deserialized);
echo $reserialized . "\n";  // 1,2,#,#,3,4,#,#,5,#,#

3. Path Finding

# filename: tree-path-finder.php
<?php

declare(strict_types=1);

class TreePathFinder
{
    // Find all root-to-leaf paths
    public function findAllPaths(?TreeNode $root): array
    {
        $paths = [];
        $this->findPathsHelper($root, [], $paths);
        return $paths;
    }

    private function findPathsHelper(?TreeNode $node, array $currentPath, array &$paths): void
    {
        if ($node === null) {
            return;
        }

        $currentPath[] = $node->data;

        // Leaf node
        if ($node->left === null && $node->right === null) {
            $paths[] = $currentPath;
            return;
        }

        $this->findPathsHelper($node->left, $currentPath, $paths);
        $this->findPathsHelper($node->right, $currentPath, $paths);
    }

    // Find path to a specific node
    public function findPathToNode(?TreeNode $root, mixed $target): ?array
    {
        $path = [];
        if ($this->findPathHelper($root, $target, $path)) {
            return $path;
        }
        return null;
    }

    private function findPathHelper(?TreeNode $node, mixed $target, array &$path): bool
    {
        if ($node === null) {
            return false;
        }

        $path[] = $node->data;

        if ($node->data === $target) {
            return true;
        }

        if ($this->findPathHelper($node->left, $target, $path) ||
            $this->findPathHelper($node->right, $target, $path)) {
            return true;
        }

        array_pop($path);  // Backtrack
        return false;
    }

    // Find paths with given sum
    public function findPathsWithSum(?TreeNode $root, int $targetSum): array
    {
        $paths = [];
        $this->findSumPathsHelper($root, $targetSum, [], $paths);
        return $paths;
    }

    private function findSumPathsHelper(
        ?TreeNode $node,
        int $targetSum,
        array $currentPath,
        array &$paths
    ): void {
        if ($node === null) {
            return;
        }

        $currentPath[] = $node->data;
        $currentSum = array_sum($currentPath);

        // Leaf node with target sum
        if ($node->left === null && $node->right === null && $currentSum === $targetSum) {
            $paths[] = $currentPath;
            return;
        }

        $this->findSumPathsHelper($node->left, $targetSum, $currentPath, $paths);
        $this->findSumPathsHelper($node->right, $targetSum, $currentPath, $paths);
    }
}

// Example
$tree = new TreeNode(5,
    new TreeNode(4,
        new TreeNode(11,
            new TreeNode(7),
            new TreeNode(2)
        )
    ),
    new TreeNode(8,
        new TreeNode(13),
        new TreeNode(4,
            new TreeNode(5),
            new TreeNode(1)
        )
    )
);

$pathFinder = new TreePathFinder();
print_r($pathFinder->findAllPaths($tree));
print_r($pathFinder->findPathToNode($tree, 7));
print_r($pathFinder->findPathsWithSum($tree, 22));  // [[5,4,11,2], [5,8,4,5]]

Complexity Analysis

Traversal Type	Time Complexity	Space Complexity	Notes
In-Order (Recursive)	O(n)	O(h)	h = height, worst case O(n) for skewed tree
Pre-Order (Recursive)	O(n)	O(h)	Same as above
Post-Order (Recursive)	O(n)	O(h)	Same as above
Level-Order	O(n)	O(w)	w = max width, worst case O(n)
In-Order (Iterative)	O(n)	O(h)	Explicit stack
Morris Traversal	O(n)	O(1)	Temporarily modifies tree

Where:

• n = number of nodes
• h = height of tree
• w = maximum width of tree

Practical Applications

1. File System Directory Listing

# filename: filesystem-traversal.php
<?php

declare(strict_types=1);

class FileNode
{
    public function __construct(
        public string $name,
        public bool $isDirectory,
        public array $children = []
    ) {}
}

class FileSystemTraversal
{
    // List all files (DFS pre-order)
    public function listAllFiles(FileNode $root, string $prefix = ''): array
    {
        $files = [];

        $currentPath = $prefix . $root->name;

        if (!$root->isDirectory) {
            $files[] = $currentPath;
        } else {
            foreach ($root->children as $child) {
                $files = array_merge(
                    $files,
                    $this->listAllFiles($child, $currentPath . '/')
                );
            }
        }

        return $files;
    }

    // List by directory level (BFS)
    public function listByLevel(FileNode $root): array
    {
        $levels = [];
        $queue = [['node' => $root, 'level' => 0]];

        while (!empty($queue)) {
            $item = array_shift($queue);
            $node = $item['node'];
            $level = $item['level'];

            if (!isset($levels[$level])) {
                $levels[$level] = [];
            }

            $levels[$level][] = $node->name;

            if ($node->isDirectory) {
                foreach ($node->children as $child) {
                    $queue[] = ['node' => $child, 'level' => $level + 1];
                }
            }
        }

        return $levels;
    }
}

2. HTML DOM Traversal

# filename: dom-traversal.php
<?php

declare(strict_types=1);

class DOMNode
{
    public function __construct(
        public string $tag,
        public array $attributes = [],
        public array $children = [],
        public ?string $text = null
    ) {}
}

class DOMTraversal
{
    // Find all elements with specific tag (DFS)
    public function findByTag(DOMNode $root, string $tag): array
    {
        $elements = [];

        if ($root->tag === $tag) {
            $elements[] = $root;
        }

        foreach ($root->children as $child) {
            $elements = array_merge($elements, $this->findByTag($child, $tag));
        }

        return $elements;
    }

    // Find elements with specific attribute
    public function findByAttribute(DOMNode $root, string $attr, mixed $value = null): array
    {
        $elements = [];

        if (isset($root->attributes[$attr])) {
            if ($value === null || $root->attributes[$attr] === $value) {
                $elements[] = $root;
            }
        }

        foreach ($root->children as $child) {
            $elements = array_merge($elements, $this->findByAttribute($child, $attr, $value));
        }

        return $elements;
    }

    // Render HTML (pre-order traversal)
    public function render(DOMNode $node, int $indent = 0): string
    {
        $html = str_repeat('  ', $indent);
        $html .= '<' . $node->tag;

        foreach ($node->attributes as $key => $value) {
            $html .= " {$key}=\"{$value}\"";
        }

        if (empty($node->children) && $node->text === null) {
            $html .= " />\n";
        } else {
            $html .= '>';

            if ($node->text !== null) {
                $html .= $node->text;
            } else {
                $html .= "\n";
                foreach ($node->children as $child) {
                    $html .= $this->render($child, $indent + 1);
                }
                $html .= str_repeat('  ', $indent);
            }

            $html .= "</{$node->tag}>\n";
        }

        return $html;
    }
}

Best Practices

1. Choose the Right Traversal

   • In-order: BST operations, sorted output
   • Pre-order: Tree copying, prefix expressions
   • Post-order: Tree deletion, postfix expressions
   • Level-order: Level-wise processing, shortest path

2. Iterative vs Recursive

   • Recursive: Cleaner code, easier to understand
   • Iterative: Better for deep trees (avoid stack overflow)

3. Space Optimization

   • Use Morris traversal when O(1) space is critical
   • Be aware it temporarily modifies the tree

4. Error Handling

   • Always check for null nodes
   • Handle empty trees gracefully

Advanced Traversal Variations

Vertical Order Traversal

Vertical order traversal groups nodes by their horizontal distance from the root. Nodes at the same horizontal distance appear in the same vertical line.

# filename: vertical-order-traversal.php
<?php

declare(strict_types=1);

class TreeTraversal
{
    public function verticalOrder(?TreeNode $root): array
    {
        if ($root === null) {
            return [];
        }

        $map = [];
        $queue = [['node' => $root, 'hd' => 0]];  // hd = horizontal distance

        while (!empty($queue)) {
            $item = array_shift($queue);
            $node = $item['node'];
            $hd = $item['hd'];

            if (!isset($map[$hd])) {
                $map[$hd] = [];
            }
            $map[$hd][] = $node->data;

            if ($node->left !== null) {
                $queue[] = ['node' => $node->left, 'hd' => $hd - 1];
            }
            if ($node->right !== null) {
                $queue[] = ['node' => $node->right, 'hd' => $hd + 1];
            }
        }

        ksort($map);
        return array_values($map);
    }
}

Boundary Traversal

Boundary traversal prints the left boundary, all leaves, and the right boundary in counterclockwise order.

# filename: boundary-traversal.php
<?php

declare(strict_types=1);

class TreeTraversal
{
    public function boundaryTraversal(?TreeNode $root): array
    {
        if ($root === null) {
            return [];
        }

        $result = [$root->data];

        // Left boundary (excluding leaf)
        $this->leftBoundary($root->left, $result);

        // All leaves
        $this->leaves($root->left, $result);
        $this->leaves($root->right, $result);

        // Right boundary (excluding leaf, in reverse)
        $rightBoundary = [];
        $this->rightBoundary($root->right, $rightBoundary);
        $result = array_merge($result, array_reverse($rightBoundary));

        return $result;
    }

    private function leftBoundary(?TreeNode $node, array &$result): void
    {
        if ($node === null || ($node->left === null && $node->right === null)) {
            return;
        }

        $result[] = $node->data;

        if ($node->left !== null) {
            $this->leftBoundary($node->left, $result);
        } else {
            $this->leftBoundary($node->right, $result);
        }
    }

    private function rightBoundary(?TreeNode $node, array &$result): void
    {
        if ($node === null || ($node->left === null && $node->right === null)) {
            return;
        }

        $result[] = $node->data;

        if ($node->right !== null) {
            $this->rightBoundary($node->right, $result);
        } else {
            $this->rightBoundary($node->left, $result);
        }
    }

    private function leaves(?TreeNode $node, array &$result): void
    {
        if ($node === null) {
            return;
        }

        if ($node->left === null && $node->right === null) {
            $result[] = $node->data;
            return;
        }

        $this->leaves($node->left, $result);
        $this->leaves($node->right, $result);
    }
}

Tree Views

Tree view problems find nodes visible from different perspectives.

# filename: tree-views.php
<?php

declare(strict_types=1);

class TreeTraversal
{
    // Right side view: Last node at each level
    public function rightSideView(?TreeNode $root): array
    {
        if ($root === null) {
            return [];
        }

        $result = [];
        $queue = [$root];

        while (!empty($queue)) {
            $levelSize = count($queue);
            for ($i = 0; $i < $levelSize; $i++) {
                $node = array_shift($queue);
                if ($i === $levelSize - 1) {
                    $result[] = $node->data;  // Last node of level
                }
                if ($node->left !== null) $queue[] = $node->left;
                if ($node->right !== null) $queue[] = $node->right;
            }
        }

        return $result;
    }

    // Left side view: First node at each level
    public function leftSideView(?TreeNode $root): array
    {
        if ($root === null) {
            return [];
        }

        $result = [];
        $queue = [$root];

        while (!empty($queue)) {
            $levelSize = count($queue);
            $result[] = $queue[0]->data;  // First node of level

            for ($i = 0; $i < $levelSize; $i++) {
                $node = array_shift($queue);
                if ($node->left !== null) $queue[] = $node->left;
                if ($node->right !== null) $queue[] = $node->right;
            }
        }

        return $result;
    }
}

Practice Exercises

1. Basic Traversals

   • Implement all four traversals (in/pre/post/level-order) both recursively and iteratively
   • Verify outputs match for the same tree

2. Reverse Traversals

   • Implement reverse in-order traversal for descending order output
   • Compare performance with standard in-order

3. Iterator Pattern

   • Make your tree class implement Iterator interface
   • Support different traversal types via constructor parameter

4. Generator Traversals

   • Convert recursive traversals to use PHP generators
   • Measure memory usage difference for large trees

5. Advanced Variations

   • Implement vertical order traversal
   • Implement boundary traversal
   • Implement diagonal traversal
   • Implement all four view problems (right/left/top/bottom)

Wrap-up

You've completed this chapter on tree traversal algorithms! Here's what you've accomplished:

• ✓ Mastered in-order, pre-order, and post-order depth-first traversals
• ✓ Implemented level-order (breadth-first) traversal using queues
• ✓ Built both recursive and iterative versions of each traversal method
• ✓ Learned reverse traversals for descending order output
• ✓ Implemented Iterator pattern for foreach compatibility
• ✓ Created generator-based traversals for memory efficiency
• ✓ Learned Morris traversal for O(1) space complexity
• ✓ Applied traversals to solve practical problems like expression evaluation and tree serialization
• ✓ Implemented advanced variations: vertical order, boundary traversal, and tree views
• ✓ Understood when to use each traversal strategy based on problem requirements

Tree traversal is fundamental to working with trees and forms the basis for many advanced tree algorithms. The ability to systematically visit nodes in different orders gives you powerful tools for processing hierarchical data structures.

Key Takeaways

• Tree traversal systematically visits every node exactly once
• Depth-first (in/pre/post-order) uses stack, breadth-first (level-order) uses queue
• Recursive implementations are simpler but use call stack space
• Iterative implementations have explicit control over memory usage
• Morris traversal achieves O(1) space by threading the tree
• Choose traversal based on the problem: sorted output (in-order), copying (pre-order), deletion (post-order), level processing (level-order)
• Understanding traversal is fundamental for tree algorithms

Further Reading

• Binary Tree Traversal on GeeksforGeeks — Comprehensive guide to tree traversals
• Morris Traversal Algorithm — Detailed explanation of O(1) space traversal
• Tree Traversal Visualization — Interactive visualization of different traversal methods
• Chapter 18: Trees & Binary Search Trees — Review tree fundamentals

Tree Traversal Algorithms complete!Check the box when you've finished reading, or scroll to the bottom to auto-complete.

## 💻 Code Samples

All code examples from this chapter are available in the GitHub repository:

View Chapter 19 Code Samples

Clone the repository to run examples:

git clone https://github.com/dalehurley/codewithphp.git
cd codewithphp/code-samples/php-algorithms/chapter-19
php 01-*.php

Next Steps

In the next chapter, we'll explore balanced trees including AVL trees and Red-Black trees, which maintain logarithmic height for optimal operation performance.