01: Algorithm Complexity & Big O Notation

Algorithm Complexity & Big O Notation Intermediate

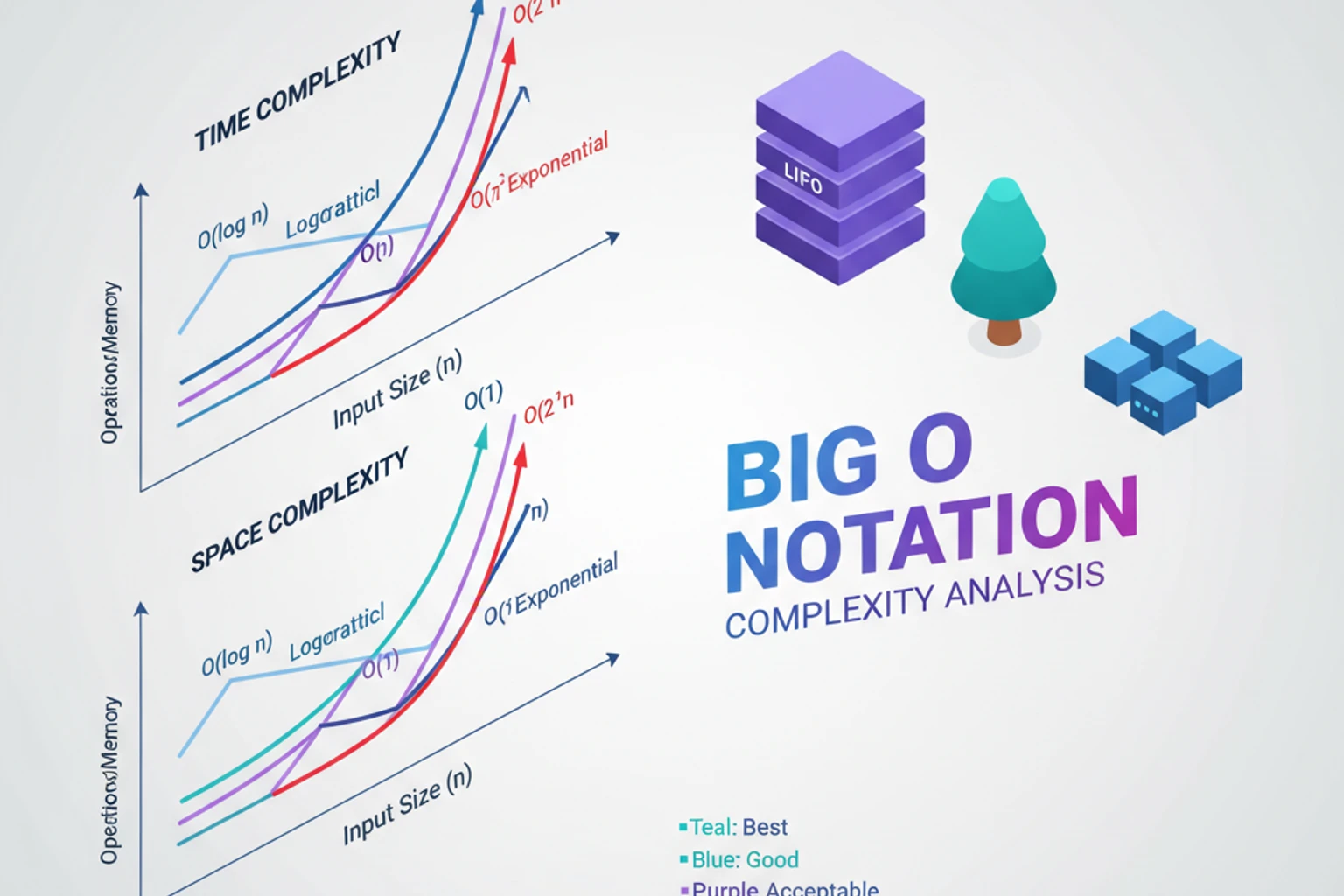
In the previous chapter, we saw that some algorithms are faster than others. But how do we measure and compare algorithm efficiency? Enter Big O notation—the language we use to describe how algorithms scale.

What You’ll Learn

Estimated time: 60 minutes

By the end of this chapter, you will:

• Master Big O notation to analyze algorithm efficiency mathematically
• Understand time and space complexity with practical PHP examples and real-world scenarios
• Learn to calculate complexity for nested loops, recursion, and built-in PHP functions
• Recognize common complexity patterns (O(1), O(n), O(n²), etc.) and when to use each
• Apply complexity analysis to security considerations and avoid performance pitfalls

Prerequisites

Before starting this chapter, ensure you have:

• ✓ Understanding of basic PHP syntax (10 mins review if needed)
• ✓ Familiarity with loops and functions (10 mins review if needed)
• ✓ Completion of Chapter 0 (45 mins if not done)

Why Algorithm Complexity Matters

Imagine you’re building a user search feature for your PHP application:

// Version 1: Linear search - O(n)
function findUserLinear(array $users, string $email): ?array
{
    foreach ($users as $user) {
        if ($user['email'] === $email) {
            return $user;
        }
    }
    return null;
}

// Version 2: Hash lookup - O(1)
function findUserHash(array $usersByEmail, string $email): ?array
{
    return $usersByEmail[$email] ?? null;
}

With 10 users, both versions feel instant. But with 1,000,000 users:

• Linear search: Might check 500,000 users on average
• Hash lookup: Always checks ~1 user

This is why complexity analysis matters—it predicts how your code performs as data grows.

What Is Big O Notation?

Big O notation describes how an algorithm’s runtime or memory usage grows relative to input size. It answers: “As my input gets larger, how much slower does my code get?”

The Basics

Big O uses this format: O(expression)

• O(1): Constant time—stays the same regardless of input size
• O(n): Linear time—grows proportionally with input size
• O(n²): Quadratic time—grows with the square of input size

The n represents input size (number of elements, string length, etc.).

An Analogy

Think of Big O like describing how long it takes to find a book:

• O(1): You know exactly where it is—grab it instantly
• O(log n): Use the library catalog to narrow down the section
• O(n): Check every shelf one by one
• O(n²): Check every shelf, and for each book, flip through every page

Common Time Complexities

Let’s explore the most common complexities you’ll encounter:

O(1) - Constant Time

Operations that take the same time regardless of input size:

// Array access by key - O(1)
function getFirstElement(array $arr): mixed
{
    return $arr[0];
}

// Hash table lookup - O(1)
function getUserById(array $users, int $id): ?array
{
    return $users[$id] ?? null;
}

// Simple arithmetic - O(1)
function calculateDiscount(float $price): float
{
    return $price * 0.1;
}

Key insight: The operation takes the same amount of time whether you have 10 items or 10 million.

O(log n) - Logarithmic Time

Algorithms that halve the problem size with each step:

// Binary search - O(log n)
function binarySearch(array $sorted, int $target): int|false
{
    $left = 0;
    $right = count($sorted) - 1;

    while ($left <= $right) {
        $mid = (int)(($left + $right) / 2);

        if ($sorted[$mid] === $target) {
            return $mid;
        } elseif ($sorted[$mid] < $target) {
            $left = $mid + 1;
        } else {
            $right = $mid - 1;
        }
    }

    return false;
}

// Searching 1,000,000 items takes only ~20 steps!
$numbers = range(1, 1000000);
$index = binarySearch($numbers, 742518);

Key insight: Doubling the input size only adds one more step. Very efficient!

O(n) - Linear Time

Algorithms that process each element once:

// Sum array - O(n)
function sum(array $numbers): int|float
{
    $total = 0;
    foreach ($numbers as $number) {
        $total += $number;
    }
    return $total;
}

// Find maximum - O(n)
function findMax(array $numbers): int|float
{
    $max = $numbers[0];
    foreach ($numbers as $number) {
        if ($number > $max) {
            $max = $number;
        }
    }
    return $max;
}

// Filter array - O(n)
function filterEven(array $numbers): array
{
    $result = [];
    foreach ($numbers as $number) {
        if ($number % 2 === 0) {
            $result[] = $number;
        }
    }
    return $result;
}

Key insight: Doubling the input size doubles the runtime.

O(n log n) - Linearithmic Time

Efficient sorting algorithms fall into this category:

// Merge sort - O(n log n)
function mergeSort(array $arr): array
{
    if (count($arr) <= 1) {
        return $arr;
    }

    $mid = (int)(count($arr) / 2);
    $left = mergeSort(array_slice($arr, 0, $mid));
    $right = mergeSort(array_slice($arr, $mid));

    return merge($left, $right);
}

function merge(array $left, array $right): array
{
    $result = [];
    $i = $j = 0;

    while ($i < count($left) && $j < count($right)) {
        if ($left[$i] <= $right[$j]) {
            $result[] = $left[$i++];
        } else {
            $result[] = $right[$j++];
        }
    }

    return array_merge($result, array_slice($left, $i), array_slice($right, $j));
}

Key insight: Much faster than O(n²) for sorting, but slower than O(n).

O(n²) - Quadratic Time

Nested loops over the same data:

// Bubble sort - O(n²)
function bubbleSort(array $arr): array
{
    $n = count($arr);

    for ($i = 0; $i < $n - 1; $i++) {
        for ($j = 0; $j < $n - $i - 1; $j++) {
            if ($arr[$j] > $arr[$j + 1]) {
                [$arr[$j], $arr[$j + 1]] = [$arr[$j + 1], $arr[$j]];
            }
        }
    }

    return $arr;
}

// Find all pairs - O(n²)
function findAllPairs(array $items): array
{
    $pairs = [];

    for ($i = 0; $i < count($items); $i++) {
        for ($j = $i + 1; $j < count($items); $j++) {
            $pairs[] = [$items[$i], $items[$j]];
        }
    }

    return $pairs;
}

Key insight: Doubling the input size quadruples the runtime. Gets slow quickly!

O(2ⁿ) - Exponential Time

Algorithms that double in runtime with each additional input:

// Fibonacci (naive recursive) - O(2ⁿ)
function fibonacci(int $n): int
{
    if ($n <= 1) {
        return $n;
    }

    return fibonacci($n - 1) + fibonacci($n - 2);
}

// This is VERY slow for large n!
// fibonacci(40) might take seconds
// fibonacci(50) might take hours!

Key insight: Avoid exponential algorithms for anything but tiny inputs.

Complexity Comparison Chart

Here’s how these complexities compare with different input sizes:

n (input)	O(1)	O(log n)	O(n)	O(n log n)	O(n²)	O(2ⁿ)
10	1	3	10	33	100	1,024
100	1	7	100	664	10,000	~10³⁰
1,000	1	10	1,000	9,966	1M	∞
10,000	1	13	10K	130K	100M	∞

Notice how O(2ⁿ) becomes unusable very quickly!

Space Complexity

Big O also describes memory usage:

// O(1) space - only uses a fixed amount of extra memory
function sumArray(array $numbers): int
{
    $total = 0; // Only one variable
    foreach ($numbers as $number) {
        $total += $number;
    }
    return $total;
}

// O(n) space - creates a new array proportional to input
function doubleValues(array $numbers): array
{
    $doubled = []; // New array grows with input
    foreach ($numbers as $number) {
        $doubled[] = $number * 2;
    }
    return $doubled;
}

// O(n) space - recursive call stack
function factorial(int $n): int
{
    if ($n <= 1) {
        return 1;
    }
    return $n * factorial($n - 1); // Stack grows with n
}

Analyzing Real PHP Code

Let’s analyze complexity for a practical example:

class UserRepository
{
    private array $users = [];

    // O(1) - direct array access
    public function findById(int $id): ?array
    {
        return $this->users[$id] ?? null;
    }

    // O(n) - must check each user
    public function findByEmail(string $email): ?array
    {
        foreach ($this->users as $user) {
            if ($user['email'] === $email) {
                return $user;
            }
        }
        return null;
    }

    // O(n) - must process each user
    public function findActive(): array
    {
        $active = [];
        foreach ($this->users as $user) {
            if ($user['active']) {
                $active[] = $user;
            }
        }
        return $active;
    }

    // O(n²) - nested loops!
    public function findCommonFriends(int $userId1, int $userId2): array
    {
        $user1Friends = $this->users[$userId1]['friends'];
        $user2Friends = $this->users[$userId2]['friends'];
        $common = [];

        foreach ($user1Friends as $friend1) {
            foreach ($user2Friends as $friend2) {
                if ($friend1 === $friend2) {
                    $common[] = $friend1;
                }
            }
        }

        return $common;
    }

    // Better: O(n) using hash lookup
    public function findCommonFriendsOptimized(int $userId1, int $userId2): array
    {
        $user1Friends = $this->users[$userId1]['friends'];
        $user2Friends = $this->users[$userId2]['friends'];

        // Create hash set - O(n)
        $friendSet = array_flip($user1Friends);

        // Check membership - O(n)
        $common = [];
        foreach ($user2Friends as $friend) {
            if (isset($friendSet[$friend])) {
                $common[] = $friend;
            }
        }

        return $common;
    }
}

Rules for Calculating Big O

Rule 1: Drop Constants

O(2n) → O(n) O(500) → O(1)

// Both are O(n), even though one does twice the work
function example1(array $arr): void {
    foreach ($arr as $item) { }
}

function example2(array $arr): void {
    foreach ($arr as $item) { }
    foreach ($arr as $item) { }
}

Rule 2: Drop Non-Dominant Terms

O(n² + n) → O(n²) O(n + log n) → O(n)

// This is O(n²), not O(n² + n)
function example(array $arr): void {
    foreach ($arr as $item) { } // O(n)

    foreach ($arr as $item1) {  // O(n²)
        foreach ($arr as $item2) { }
    }
}

Rule 3: Different Inputs = Different Variables

// This is O(a + b), not O(n)
function mergeTwoArrays(array $a, array $b): array {
    $result = [];

    foreach ($a as $item) {
        $result[] = $item;
    }

    foreach ($b as $item) {
        $result[] = $item;
    }

    return $result;
}

// This is O(a * b), not O(n²)
function findCommonElements(array $a, array $b): array {
    $common = [];

    foreach ($a as $itemA) {
        foreach ($b as $itemB) {
            if ($itemA === $itemB) {
                $common[] = $itemA;
            }
        }
    }

    return $common;
}

Best, Worst, and Average Case

Some algorithms have different complexities depending on input:

function linearSearch(array $arr, $target): int|false
{
    foreach ($arr as $index => $value) {
        if ($value === $target) {
            return $index;
        }
    }
    return false;
}

// Best case: O(1) - target is first element
// Worst case: O(n) - target is last or not present
// Average case: O(n/2) → O(n)

We typically focus on worst-case complexity because it guarantees performance.

Practical Tips for PHP Developers

1. Know Your Built-in Functions

// in_array() - O(n)
if (in_array($needle, $haystack)) { }

// isset() - O(1) for arrays
if (isset($array[$key])) { }

// array_search() - O(n)
$key = array_search($value, $array);

// sort() - O(n log n)
sort($array);

2. Use Hash Lookups When Possible

// Bad: O(n) for each check
$validEmails = ['user1@example.com', 'user2@example.com'];
if (in_array($email, $validEmails)) { }

// Good: O(1) for each check
$validEmails = [
    'user1@example.com' => true,
    'user2@example.com' => true
];
if (isset($validEmails[$email])) { }

3. Watch for Hidden Loops

// This looks like O(n) but is actually O(n²)!
function joinWithCommas(array $items): string
{
    $result = '';
    foreach ($items as $item) {
        $result .= $item . ','; // String concatenation is O(n)
    }
    return rtrim($result, ',');
}

// Better: O(n)
function joinWithCommas(array $items): string
{
    return implode(',', $items);
}

Amortized Complexity

Sometimes an operation is expensive occasionally but cheap most of the time. Amortized analysis considers the average cost over a sequence of operations.

Dynamic Array Example

class DynamicArray
{
    private array $data = [];
    private int $size = 0;
    private int $capacity = 1;

    public function append($value): void
    {
        // If array is full, double the capacity
        if ($this->size === $this->capacity) {
            $this->resize($this->capacity * 2); // Expensive O(n) operation
        }

        $this->data[$this->size++] = $value;
    }

    private function resize(int $newCapacity): void
    {
        $newData = [];
        for ($i = 0; $i < $this->size; $i++) {
            $newData[$i] = $this->data[$i];
        }
        $this->data = $newData;
        $this->capacity = $newCapacity;
    }
}

// Individual append: O(1) usually, O(n) occasionally
// Amortized complexity: O(1) per append

Why O(1) amortized?

• Resize happens at sizes: 1, 2, 4, 8, 16, 32…
• For n appends, you copy: 1 + 2 + 4 + 8 + … + n/2 = n-1 elements total
• Average: (n-1)/n ≈ 1 copy per append → O(1) amortized

PHP’s Array Implementation

PHP arrays use this strategy internally:

// PHP arrays have amortized O(1) append
$arr = [];
for ($i = 0; $i < 1000000; $i++) {
    $arr[] = $i; // Amortized O(1), not O(n) each time!
}

Common Mistakes in Complexity Analysis

Mistake 1: Confusing Best, Worst, and Average Cases

function findElement(array $arr, $target): bool
{
    foreach ($arr as $item) {
        if ($item === $target) {
            return true; // Might return early
        }
    }
    return false;
}

// WRONG: "This is O(1) because it might find it immediately"
// CORRECT: Worst case is O(n), which is what we report

Rule: Unless specified, always report worst-case complexity.

Mistake 2: Ignoring Hidden Complexity

// This looks like O(n) but is actually O(n²)!
function buildString(array $words): string
{
    $result = '';
    foreach ($words as $word) {
        $result .= $word; // String concatenation creates new string: O(n)
    }
    return $result;
}

// Each concatenation copies the entire string
// Total: 0 + len(word1) + len(word1+word2) + ... = O(n²)

Mistake 3: Not Considering Input Characteristics

// Complexity depends on BOTH array sizes
function findCommonElements(array $a, array $b): array
{
    $common = [];
    foreach ($a as $itemA) {
        foreach ($b as $itemB) {
            if ($itemA === $itemB) {
                $common[] = $itemA;
            }
        }
    }
    return $common;
}

// WRONG: O(n²)
// CORRECT: O(a × b) where a = len($a), b = len($b)

Mistake 4: Calling count() in Loops

// Inefficient: count() called n times
for ($i = 0; $i < count($arr); $i++) {
    // If count() is O(n), this becomes O(n²)!
}

// Efficient: cache the count
$n = count($arr);
for ($i = 0; $i < $n; $i++) {
    // O(n)
}

Note: In PHP, count() is O(1) for regular arrays, but O(n) for some objects implementing Countable.

Security Considerations

Algorithm complexity affects security, not just performance.

Algorithmic Complexity Attacks

Attackers can exploit O(n²) or worse algorithms to cause denial of service:

// Vulnerable to hash collision attacks
class VulnerableCache
{
    private array $cache = [];

    public function add(string $key, $value): void
    {
        // If attacker finds hash collisions, this degrades to O(n)
        $this->cache[$key] = $value;
    }

    public function get(string $key)
    {
        return $this->cache[$key] ?? null;
    }
}

// Better: Use cryptographically secure hashing or rate limiting

ReDoS (Regular Expression Denial of Service)

// Vulnerable: catastrophic backtracking O(2ⁿ)
function validateEmail_VULNERABLE(string $email): bool
{
    // Pattern with nested quantifiers
    return (bool)preg_match('/^([a-zA-Z0-9]+)+@[a-zA-Z]+\.com$/', $email);
}

// Attack: "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaa!" takes exponential time

// Safe: Avoid nested quantifiers
function validateEmail_SAFE(string $email): bool
{
    return (bool)preg_match('/^[a-zA-Z0-9]+@[a-zA-Z]+\.com$/', $email);
}

Input Validation

Always validate input size to prevent resource exhaustion:

function processArray(array $data): array
{
    // Prevent attacks with huge inputs
    if (count($data) > 10000) {
        throw new InvalidArgumentException('Input too large');
    }

    // Your O(n²) algorithm is now bounded
    return someExpensiveOperation($data);
}

Advanced PHP Performance Tips

Tip 4: Array Functions vs Loops

// Benchmark reveals: loops are often faster for simple operations
$bench = new Benchmark();
$data = range(1, 10000);

$bench->compare([
    'array_map' => fn() => array_map(fn($x) => $x * 2, $data),
    'foreach loop' => function() use ($data) {
        $result = [];
        foreach ($data as $x) {
            $result[] = $x * 2;
        }
        return $result;
    },
], null, 100);

// Loops often win for simple operations due to function call overhead

Tip 5: Generator for Memory Efficiency

// Memory-intensive: O(n) space
function rangeArray(int $start, int $end): array
{
    $result = [];
    for ($i = $start; $i <= $end; $i++) {
        $result[] = $i;
    }
    return $result;
}

// Memory-efficient: O(1) space
function rangeGenerator(int $start, int $end): Generator
{
    for ($i = $start; $i <= $end; $i++) {
        yield $i;
    }
}

// Process 1 million items without using 1 million items of memory
foreach (rangeGenerator(1, 1000000) as $num) {
    processItem($num);
}

Tip 6: Opcode Cache Impact

// With OPcache enabled, code is compiled once
// This can significantly affect benchmarks

// Always benchmark with production-like settings:
// - OPcache enabled
// - JIT enabled (PHP 8.0+)
// - Production error reporting levels

Edge Cases to Consider

Empty Input

function findMax(array $numbers): int|float
{
    // Bug: Crashes on empty array
    // return max($numbers);

    // Fixed: Handle edge case
    if (empty($numbers)) {
        throw new InvalidArgumentException('Array cannot be empty');
    }
    return max($numbers);
}

Single Element

function binarySearch(array $arr, $target): int|false
{
    // Edge case: single element
    if (count($arr) === 1) {
        return $arr[0] === $target ? 0 : false;
    }

    // Main algorithm...
}

Very Large Numbers

function factorial(int $n): int
{
    // Edge case: integer overflow for large n
    if ($n > 20) {
        throw new OverflowException('Result would overflow');
    }

    // Use GMP for arbitrary precision if needed
    // return gmp_fact($n);

    $result = 1;
    for ($i = 2; $i <= $n; $i++) {
        $result *= $i;
    }
    return $result;
}

Negative Numbers

function power(int $base, int $exponent): int|float
{
    // Edge case: negative exponent
    if ($exponent < 0) {
        return 1 / power($base, -$exponent);
    }

    if ($exponent === 0) {
        return 1;
    }

    return $base * power($base, $exponent - 1);
}

Practice Problems

Problem 1: Analyze This Code

What’s the time complexity?

function mystery(array $arr): int
{
    $count = 0;

    for ($i = 0; $i < count($arr); $i++) {
        if ($arr[$i] % 2 === 0) {
            $count++;
        }
    }

    for ($i = 0; $i < count($arr); $i++) {
        if ($arr[$i] % 3 === 0) {
            $count++;
        }
    }

    return $count;
}

Answer

O(n) - Two sequential loops, each O(n), so O(n + n) = O(n)

Problem 2: Optimize This

Improve the complexity:

// Current: O(n²)
function hasDuplicate(array $arr): bool
{
    for ($i = 0; $i < count($arr); $i++) {
        for ($j = $i + 1; $j < count($arr); $j++) {
            if ($arr[$i] === $arr[$j]) {
                return true;
            }
        }
    }
    return false;
}

Solution

// Optimized: O(n)
function hasDuplicate(array $arr): bool
{
    $seen = [];
    foreach ($arr as $value) {
        if (isset($seen[$value])) {
            return true;
        }
        $seen[$value] = true;
    }
    return false;
}

Problem 3: Identify the Complexity

What’s the complexity of this nested loop?

function printPairs(int $n): void
{
    for ($i = 0; $i < $n; $i++) {
        for ($j = $i; $j < $n; $j++) {
            echo "($i, $j) ";
        }
    }
}

Answer

O(n²) - Even though inner loop starts at $i, total iterations:

• i=0: n iterations
• i=1: n-1 iterations
• i=2: n-2 iterations
• …
• Total: n + (n-1) + (n-2) + … + 1 = n(n+1)/2 ≈ n²/2 → O(n²)

Problem 4: Space Complexity

What’s the space complexity?

function fibonacci(int $n, array $memo = []): int
{
    if ($n <= 1) return $n;
    if (isset($memo[$n])) return $memo[$n];

    $memo[$n] = fibonacci($n - 1, $memo) + fibonacci($n - 2, $memo);
    return $memo[$n];
}

Answer

O(n) space:

• Memoization array stores n values: O(n)
• Call stack depth: O(n)
• Total: O(n)

Problem 5: Real-World Optimization

Optimize this function that checks if any email in a list is valid:

// Current: O(n × m) where m is average email length
function hasValidEmail(array $emails): bool
{
    foreach ($emails as $email) {
        if (filter_var($email, FILTER_VALIDATE_EMAIL)) {
            return true;
        }
    }
    return false;
}

Answer

This is already optimal - O(n) in best/average case, O(n × m) in worst case where no valid email is found. The complexity is unavoidable since we must check emails until we find a valid one. However, we can add optimizations:

function hasValidEmail(array $emails): bool
{
    // Quick check: if empty, return false
    if (empty($emails)) {
        return false;
    }

    // Optimization: check shorter emails first (faster validation)
    usort($emails, fn($a, $b) => strlen($a) <=> strlen($b));

    foreach ($emails as $email) {
        // Skip obviously invalid (O(1) check before expensive validation)
        if (strpos($email, '@') === false) {
            continue;
        }

        if (filter_var($email, FILTER_VALIDATE_EMAIL)) {
            return true;
        }
    }
    return false;
}

Note: Sorting adds O(n log n) but can reduce average case if validation is expensive.

Problem 6: Hidden Complexity

What’s wrong with this code’s complexity?

function removeDuplicates(array $arr): array
{
    $result = [];
    foreach ($arr as $item) {
        if (!in_array($item, $result)) {
            $result[] = $item;
        }
    }
    return $result;
}

Answer

This is O(n²) because in_array() is O(n), called n times.

Optimized O(n) solution:

function removeDuplicates(array $arr): array
{
    return array_values(array_unique($arr));
    // Or manually:
    // return array_keys(array_flip($arr)); // O(n)
}

Key Takeaways

• Big O notation describes how algorithms scale with input size
• Focus on worst-case complexity for reliable performance guarantees
• Common complexities: O(1) < O(log n) < O(n) < O(n log n) < O(n²) < O(2ⁿ)
• Space complexity is just as important as time complexity
• Optimize smartly: Profile first, then optimize bottlenecks
• Know your tools: Understand PHP’s built-in function complexities

What’s Next

In the next chapter, we’ll build a benchmarking framework to actually measure algorithm performance in PHP. You’ll learn to validate your complexity analysis with real data.

💻 Code Samples

All code examples from this chapter are available in the GitHub repository:

View Chapter 01 Code Samples

Files included:

• 01-complexity-examples.php - Demonstrates all major time complexity classes with working code
• 02-space-complexity.php - Shows memory usage patterns and space complexity analysis
• README.md - Complete documentation and usage guide

Clone the repository to run the examples locally:

git clone https://github.com/dalehurley/codewithphp.git
cd codewithphp/code/php-algorithms/chapter-01
php 01-complexity-examples.php

---

Continue to Chapter 02: Benchmarking & Performance Testing.