03: Recursion Fundamentals

Recursion Fundamentals Intermediate

Overview

Recursion is one of the most powerful and elegant problem-solving techniques in computer science. A recursive function is one that calls itself to solve smaller instances of the same problem. While it may seem circular at first, recursion provides natural solutions to problems involving hierarchical data, divide-and-conquer algorithms, and backtracking scenarios.

In this chapter, you’ll develop recursive thinking—the ability to break problems down into smaller, self-similar subproblems. You’ll learn the critical elements every recursive function needs (base case and recursive case), understand how the call stack manages recursion, and master optimization techniques like memoization that transform exponential algorithms into linear ones.

By the end, you’ll confidently write recursive solutions to real-world problems including tree traversal, file system navigation, parsing, and backtracking algorithms like Sudoku solvers. You’ll also learn when recursion is the right tool and when iteration is better—a critical skill for production PHP development.

What You’ll Learn

Estimated time: 70 minutes

By the end of this chapter, you will:

• Master recursive thinking and understand how the call stack manages recursive function calls
• Learn to write correct base cases and recursive cases that make progress toward termination
• Understand when to use recursion vs iteration and their performance trade-offs
• Optimize recursive functions with memoization techniques and tail recursion patterns
• Apply recursion to real-world scenarios including tree traversal, parsing, backtracking, and divide-and-conquer

Prerequisites

Before starting this chapter, you should have:

• ✓ Understanding of functions and how they work (10 mins review from Chapter 4 if needed)
• ✓ Familiarity with the call stack concept (15 mins learning if needed)
• ✓ Completion of Chapters 0-2 or equivalent foundations (180 mins if not done)
• ✓ Basic understanding of arrays and loops

Estimated Time: ~70 minutes

What You’ll Build

By the end of this chapter, you will have created:

• A recursive factorial calculator demonstrating base case and recursive case patterns
• An optimized Fibonacci implementation using memoization (100x+ performance improvement)
• A directory tree traversal function for file system navigation
• A recursive array flattener handling deeply nested data structures
• A Sudoku solver using recursive backtracking
• A recursive descent parser for evaluating arithmetic expressions

What Is Recursion? (~5 min)

Recursion occurs when a function calls itself. It’s like looking into two mirrors facing each other—you see infinite reflections, each slightly smaller.

::: tip Recursive Thinking The key to recursion is breaking a problem into smaller versions of itself. Each recursive call should work on a simpler problem, eventually reaching a base case that stops the recursion. :::

A Simple Example

countdown.php

<?php

declare(strict_types=1);

function countdown(int $n): void
{
    if ($n <= 0) {
        echo "Blast off!\n";
        return;
    }

    echo "$n...\n";
    countdown($n - 1); // Function calls itself
}

countdown(5);

Output:

5...
4...
3...
2...
1...
Blast off!

The Two Essential Parts of Recursion (~10 min)

Every recursive function must have:

::: warning Critical Rule Every recursive function MUST have both a base case (stopping condition) and a recursive case (progress toward the base case). Missing either leads to infinite recursion and stack overflow! :::

1. Base Case (Stopping Condition)

The condition that stops the recursion. Without it, you get infinite recursion and a stack overflow!

base-case-example.php

<?php

declare(strict_types=1);

// Bad: No base case = infinite recursion
function badRecursion(int $n): int
{
    return badRecursion($n - 1); // Never stops!
}

// Good: Has base case
function goodRecursion(int $n): int
{
    if ($n <= 0) { // BASE CASE
        return 0;
    }
    return goodRecursion($n - 1); // RECURSIVE CASE
}

2. Recursive Case (Progress Toward Base Case)

The part where the function calls itself with a “smaller” problem, moving toward the base case.

factorial.php

<?php

declare(strict_types=1);

function factorial(int $n): int
{
    // Base case: factorial of 0 or 1 is 1
    if ($n <= 1) {
        return 1;
    }

    // Recursive case: n! = n × (n-1)!
    return $n * factorial($n - 1);
}

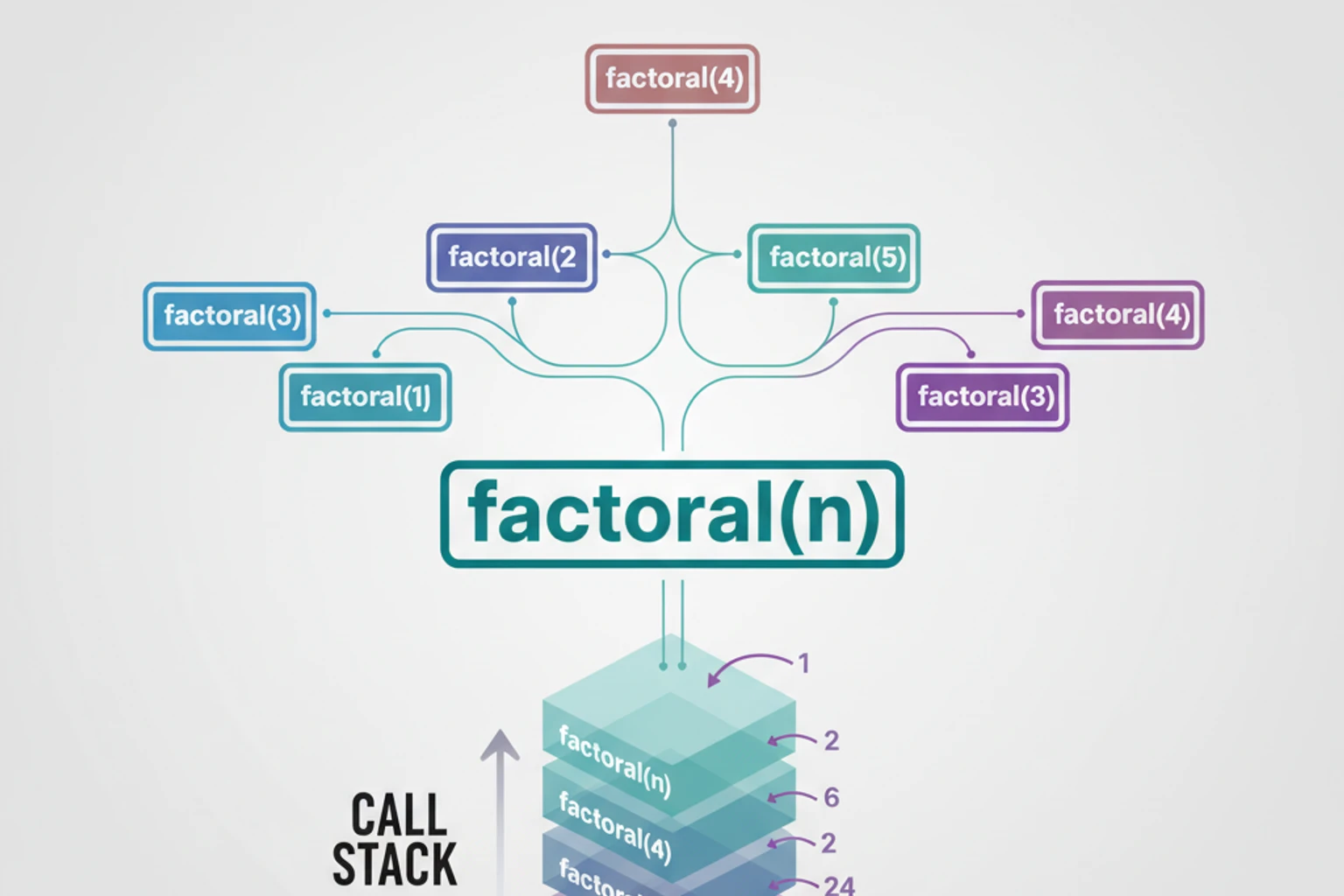
echo factorial(5); // 5 × 4 × 3 × 2 × 1 = 120

How Recursion Works: The Call Stack (~10 min)

PHP uses a call stack to track function calls:

factorial(3)
│
├─ 3 * factorial(2)
│      │
│      ├─ 2 * factorial(1)
│      │      │
│      │      └─ return 1 (base case)
│      │
│      └─ return 2 * 1 = 2
│
└─ return 3 * 2 = 6

Each function call is pushed onto the stack. When a base case is reached, calls start returning (popping off the stack).

Visualizing the Stack

visualize-factorial.php

<?php

declare(strict_types=1);

function visualizeFactorial(int $n, int $depth = 0): int
{
    $indent = str_repeat('  ', $depth);
    echo "{$indent}factorial({$n}) called\n";

    if ($n <= 1) {
        echo "{$indent}Base case reached: returning 1\n";
        return 1;
    }

    $result = $n * visualizeFactorial($n - 1, $depth + 1);
    echo "{$indent}factorial({$n}) returning {$result}\n";
    return $result;
}

visualizeFactorial(4);

Output:

factorial(4) called
  factorial(3) called
    factorial(2) called
      factorial(1) called
      Base case reached: returning 1
    factorial(2) returning 2
  factorial(3) returning 6
factorial(4) returning 24

Classic Recursive Problems (~15 min)

Fibonacci Sequence

Each number is the sum of the two preceding ones: 0, 1, 1, 2, 3, 5, 8, 13…

fibonacci-naive.php

<?php

declare(strict_types=1);

function fibonacci(int $n): int
{
    // Base cases
    if ($n === 0) return 0;
    if ($n === 1) return 1;

    // Recursive case
    return fibonacci($n - 1) + fibonacci($n - 2);
}

echo fibonacci(6); // 8

::: warning Performance Warning This naive Fibonacci implementation is O(2ⁿ)—exponentially slow! For fib(40), you’ll wait several seconds. We’ll fix this with memoization shortly. :::

Sum of Array

sum-array.php

<?php

declare(strict_types=1);

function sumArray(array $arr): int
{
    // Base case: empty array
    if (empty($arr)) {
        return 0;
    }

    // Recursive case: first element + sum of rest
    $first = array_shift($arr);
    return $first + sumArray($arr);
}

echo sumArray([1, 2, 3, 4, 5]); // 15

Power Function

power.php

<?php

declare(strict_types=1);

function power(int $base, int $exponent): int
{
    // Base case: anything to the power of 0 is 1
    if ($exponent === 0) {
        return 1;
    }

    // Recursive case: base × base^(exponent-1)
    return $base * power($base, $exponent - 1);
}

echo power(2, 5); // 2^5 = 32

Reverse a String

reverse-string.php

<?php

declare(strict_types=1);

function reverseString(string $str): string
{
    // Base case: empty or single character
    if (strlen($str) <= 1) {
        return $str;
    }

    // Recursive case: last char + reverse of remaining string
    return substr($str, -1) . reverseString(substr($str, 0, -1));
}

echo reverseString('hello'); // 'olleh'

Recursion vs Iteration (~10 min)

Many recursive problems can be solved iteratively. Let’s compare:

Factorial: Recursive vs Iterative

// Recursive
function factorialRecursive(int $n): int
{
    if ($n <= 1) return 1;
    return $n * factorialRecursive($n - 1);
}

// Iterative
function factorialIterative(int $n): int
{
    $result = 1;
    for ($i = 2; $i <= $n; $i++) {
        $result *= $i;
    }
    return $result;
}

Comparison:

• Recursive: More elegant, easier to understand for some problems
• Iterative: Usually faster, uses less memory (no stack overhead)

When to Use Recursion

✅ Use recursion when:

• Problem naturally divides into smaller subproblems (tree traversal, divide-and-conquer)
• Code is clearer and more maintainable
• Stack depth won’t be excessive

❌ Avoid recursion when:

• Simple iteration is clearer
• Stack depth could be very deep (risk of stack overflow)
• Performance is critical and iteration is faster

Optimizing Recursion: Tail Recursion (~5 min)

Tail recursion occurs when the recursive call is the last operation in the function. Some languages optimize this, but PHP doesn’t automatically.

::: info PHP Limitation Unlike functional languages (Scheme, Erlang), PHP doesn’t perform tail-call optimization. However, understanding tail recursion is still valuable for converting to iterative solutions. :::

// Not tail recursive: operation after recursive call
function factorial(int $n): int
{
    if ($n <= 1) return 1;
    return $n * factorial($n - 1); // Multiplication happens AFTER return
}

// Tail recursive: no operation after recursive call
function factorialTail(int $n, int $accumulator = 1): int
{
    if ($n <= 1) {
        return $accumulator;
    }
    return factorialTail($n - 1, $n * $accumulator); // Nothing after this
}

While PHP doesn’t optimize tail recursion automatically, it’s still a good pattern to know.

Common Recursive Patterns (~10 min)

1. Linear Recursion

Each function call makes one recursive call:

function countDown(int $n): void
{
    if ($n <= 0) return;
    echo "$n ";
    countDown($n - 1); // One recursive call
}

2. Binary Recursion

Each function call makes two recursive calls:

function fibonacci(int $n): int
{
    if ($n <= 1) return $n;
    return fibonacci($n - 1) + fibonacci($n - 2); // Two calls!
}

3. Multiple Recursion

Function makes many recursive calls:

function printCombinations(array $items, int $k, array $current = []): void
{
    if ($k === 0) {
        echo implode(', ', $current) . "\n";
        return;
    }

    foreach ($items as $item) {
        printCombinations($items, $k - 1, array_merge($current, [$item]));
    }
}

Recursive Data Structures (~15 min)

Some data structures are inherently recursive:

::: tip Natural Fit for Recursion Trees, nested arrays, file systems, and JSON structures are naturally recursive. Recursion often provides the clearest solution for these problems. :::

Directory Tree Traversal

function listFiles(string $directory, int $depth = 0): void
{
    $indent = str_repeat('  ', $depth);

    $items = scandir($directory);

    foreach ($items as $item) {
        if ($item === '.' || $item === '..') continue;

        $path = $directory . '/' . $item;
        echo $indent . $item . "\n";

        // Recursive case: if directory, traverse it
        if (is_dir($path)) {
            listFiles($path, $depth + 1);
        }
    }
}

listFiles('./docs');

Nested Array Sum

function sumNested(array $arr): int
{
    $sum = 0;

    foreach ($arr as $item) {
        if (is_array($item)) {
            // Recursive case: nested array
            $sum += sumNested($item);
        } else {
            // Base case: single value
            $sum += $item;
        }
    }

    return $sum;
}

$nested = [1, [2, 3, [4, 5]], 6, [7, [8, 9]]];
echo sumNested($nested); // 45

Avoiding Stack Overflow (~5 min)

PHP has a limited call stack. Deep recursion can cause stack overflow:

::: warning Stack Overflow Risk PHP’s default recursion limit is around 100-512 levels (varies by configuration). For large datasets (n > 10,000), prefer iterative solutions or tail-recursive patterns convertible to loops. :::

stack-overflow-demo.php

<?php

declare(strict_types=1);

// This will likely crash with large n
function deepRecursion(int $n): int
{
    if ($n <= 0) return 0;
    return 1 + deepRecursion($n - 1);
}

// Stack overflow!
// deepRecursion(100000);

Measuring Recursion Depth

Before deploying recursive code, measure your system’s limits:

measure-recursion-depth.php

<?php

declare(strict_types=1);

function measureRecursionDepth(int $n, int $depth = 0): int
{
    if ($n <= 0) {
        return $depth;
    }
    return measureRecursionDepth($n - 1, $depth + 1);
}

// Test your system's limit
try {
    $maxDepth = measureRecursionDepth(10000);
    echo "System supports recursion depth: {$maxDepth}\n";
} catch (Error $e) {
    echo "Recursion limit reached around depth " . substr($e->getMessage(), 0, 50) . "\n";
}

// Alternative: Use debug_backtrace() to inspect call stack
function trackRecursion(int $n): int
{
    $depth = count(debug_backtrace());
    echo "Current depth: {$depth}\n";

    if ($n <= 0) return $depth;
    return trackRecursion($n - 1);
}

// trackRecursion(5); // Shows depth increasing

Production-Safe Recursion with Error Handling

safe-recursion.php

<?php

declare(strict_types=1);

class RecursionLimitException extends RuntimeException {}

function safeRecursion(
    int $n,
    int $maxDepth = 1000,
    int $currentDepth = 0
): int {
    if ($currentDepth > $maxDepth) {
        throw new RecursionLimitException(
            "Maximum recursion depth ({$maxDepth}) exceeded at n={$n}"
        );
    }

    if ($n <= 0) {
        return 0; // Base case
    }

    return 1 + safeRecursion($n - 1, $maxDepth, $currentDepth + 1);
}

// Safe usage in production
try {
    $result = safeRecursion(500); // Safe limit
    echo "Result: {$result}\n";
} catch (RecursionLimitException $e) {
    error_log("Recursion limit error: " . $e->getMessage());
    // Fallback to iterative approach
    echo "Switching to iterative solution...\n";
}

Solution 1: Use Iteration

iterative-count.php

<?php

declare(strict_types=1);

function iterativeCount(int $n): int
{
    $count = 0;
    for ($i = 0; $i < $n; $i++) {
        $count++;
    }
    return $count;
}

echo iterativeCount(100000); // Works fine!

Solution 2: Increase Stack Size (Not Recommended)

ini_set('xdebug.max_nesting_level', 10000); // Requires Xdebug

Better to redesign with iteration or tail recursion where possible.

Memory Usage: Recursion vs Iteration

Recursive calls consume stack memory. Let’s compare:

memory-comparison.php

<?php

declare(strict_types=1);

// Recursive: Uses O(n) stack space
function sumRecursive(int $n): int
{
    if ($n <= 0) return 0;
    return $n + sumRecursive($n - 1);
}

// Iterative: Uses O(1) space
function sumIterative(int $n): int
{
    $sum = 0;
    for ($i = 1; $i <= $n; $i++) {
        $sum += $i;
    }
    return $sum;
}

// Measure memory
$n = 1000;

memory_reset_peak_usage();
$result = sumRecursive($n);
$recursiveMemory = memory_get_peak_usage();

memory_reset_peak_usage();
$result = sumIterative($n);
$iterativeMemory = memory_get_peak_usage();

echo "Recursive memory: " . number_format($recursiveMemory) . " bytes\n";
echo "Iterative memory: " . number_format($iterativeMemory) . " bytes\n";
echo "Difference: " . number_format($recursiveMemory - $iterativeMemory) . " bytes\n";

Key Takeaway: Recursion uses O(n) stack space, iteration uses O(1). For large n, this matters!

Memoization: Optimizing Recursive Functions (~10 min)

Memoization caches results to avoid redundant calculations:

::: tip Performance Boost Memoization can transform Fibonacci from O(2ⁿ) to O(n)—that’s the difference between seconds and microseconds for fib(35)! Always consider memoization for recursive functions with overlapping subproblems. :::

// Slow: O(2ⁿ) - recalculates same values
function fibonacciSlow(int $n): int
{
    if ($n <= 1) return $n;
    return fibonacciSlow($n - 1) + fibonacciSlow($n - 2);
}

// Fast: O(n) - caches results
function fibonacciFast(int $n, array &$memo = []): int
{
    if ($n <= 1) return $n;

    if (isset($memo[$n])) {
        return $memo[$n]; // Return cached result
    }

    $memo[$n] = fibonacciFast($n - 1, $memo) + fibonacciFast($n - 2, $memo);
    return $memo[$n];
}

// Compare performance
$start = microtime(true);
echo fibonacciSlow(35) . "\n"; // Takes several seconds
echo "Time: " . (microtime(true) - $start) . "s\n";

$start = microtime(true);
echo fibonacciFast(35) . "\n"; // Nearly instant!
echo "Time: " . (microtime(true) - $start) . "s\n";

We’ll explore memoization deeply in the Dynamic Programming section.

Real-World PHP Examples (~15 min)

JSON Validation

function validateJSON($data): bool
{
    if (is_scalar($data) || $data === null) {
        return true; // Base case: primitive types are valid
    }

    if (is_array($data)) {
        foreach ($data as $item) {
            if (!validateJSON($item)) { // Recursive validation
                return false;
            }
        }
        return true;
    }

    if (is_object($data)) {
        foreach ($data as $value) {
            if (!validateJSON($value)) { // Recursive validation
                return false;
            }
        }
        return true;
    }

    return false;
}

$data = ['name' => 'John', 'nested' => ['age' => 30, 'tags' => ['php', 'dev']]];
echo validateJSON($data) ? 'Valid' : 'Invalid';

Menu Hierarchy Rendering

function renderMenu(array $items, int $depth = 0): string
{
    $html = str_repeat('  ', $depth) . "<ul>\n";

    foreach ($items as $item) {
        $html .= str_repeat('  ', $depth + 1) . "<li>{$item['title']}";

        // Recursive case: render children
        if (!empty($item['children'])) {
            $html .= "\n" . renderMenu($item['children'], $depth + 2);
            $html .= str_repeat('  ', $depth + 1);
        }

        $html .= "</li>\n";
    }

    $html .= str_repeat('  ', $depth) . "</ul>\n";
    return $html;
}

$menu = [
    ['title' => 'Home', 'children' => []],
    ['title' => 'Products', 'children' => [
        ['title' => 'Electronics', 'children' => []],
        ['title' => 'Clothing', 'children' => []]
    ]],
    ['title' => 'About', 'children' => []]
];

echo renderMenu($menu);

Mutual Recursion (~5 min)

Functions can call each other recursively:

// Check if a number is even/odd using mutual recursion
function isEven(int $n): bool
{
    if ($n === 0) {
        return true;
    }
    return isOdd($n - 1);
}

function isOdd(int $n): bool
{
    if ($n === 0) {
        return false;
    }
    return isEven($n - 1);
}

echo isEven(4) ? 'true' : 'false'; // true
echo isOdd(4) ? 'true' : 'false';  // false

Practical example: State machine

interface State
{
    public function handle(string $input): ?State;
}

class ReadingState implements State
{
    public function handle(string $input): ?State
    {
        if ($input === 'START_TAG') {
            return new TagState();
        }
        return $this; // Stay in reading state
    }
}

class TagState implements State
{
    public function handle(string $input): ?State
    {
        if ($input === 'END_TAG') {
            return new ReadingState();
        }
        return $this;
    }
}

// Parser using mutually recursive states
function parseHTML(array $tokens, State $state = null): void
{
    if (empty($tokens)) {
        return;
    }

    $state = $state ?? new ReadingState();
    $token = array_shift($tokens);
    $newState = $state->handle($token);

    parseHTML($tokens, $newState); // Recursive call with new state
}

Converting Recursion to Iteration (~10 min)

Some recursive algorithms can be converted to iterative ones for better performance.

Technique 1: Using a Stack

// Recursive: Depth-first traversal
function dfsRecursive(TreeNode $node): void
{
    if ($node === null) return;

    echo $node->value . " ";
    dfsRecursive($node->left);
    dfsRecursive($node->right);
}

// Iterative: Using explicit stack
function dfsIterative(TreeNode $node): void
{
    $stack = [$node];

    while (!empty($stack)) {
        $current = array_pop($stack);

        if ($current === null) continue;

        echo $current->value . " ";

        // Push right first so left is processed first
        if ($current->right) $stack[] = $current->right;
        if ($current->left) $stack[] = $current->left;
    }
}

Technique 2: Accumulator Pattern

// Recursive: Uses call stack
function sumRecursive(array $arr): int
{
    if (empty($arr)) return 0;
    return $arr[0] + sumRecursive(array_slice($arr, 1));
}

// Iterative: Uses accumulator
function sumIterative(array $arr): int
{
    $sum = 0;
    foreach ($arr as $value) {
        $sum += $value;
    }
    return $sum;
}

// Tail-recursive with accumulator (still recursive but more efficient)
function sumTailRecursive(array $arr, int $acc = 0): int
{
    if (empty($arr)) return $acc;
    return sumTailRecursive(array_slice($arr, 1), $acc + $arr[0]);
}

Technique 3: Loop with State

// Recursive: Factorial
function factorialRecursive(int $n): int
{
    if ($n <= 1) return 1;
    return $n * factorialRecursive($n - 1);
}

// Iterative: Loop with state
function factorialIterative(int $n): int
{
    $result = 1;
    for ($i = 2; $i <= $n; $i++) {
        $result *= $i;
    }
    return $result;
}

// When to convert:
// - Deep recursion (risk of stack overflow)
// - Performance-critical code
// - When iteration is equally clear

Advanced Recursion Patterns (~15 min)

Divide and Conquer with Recursion

// Binary search - divides problem in half each time
function binarySearchRecursive(array $arr, int $target, int $left = 0, int $right = null): int
{
    if ($right === null) {
        $right = count($arr) - 1;
    }

    if ($left > $right) {
        return -1; // Not found
    }

    $mid = (int)(($left + $right) / 2);

    if ($arr[$mid] === $target) {
        return $mid;
    } elseif ($arr[$mid] < $target) {
        return binarySearchRecursive($arr, $target, $mid + 1, $right);
    } else {
        return binarySearchRecursive($arr, $target, $left, $mid - 1);
    }
}

// Merge sort - divides, sorts, then merges
function mergeSortRecursive(array $arr): array
{
    if (count($arr) <= 1) {
        return $arr;
    }

    $mid = (int)(count($arr) / 2);
    $left = mergeSortRecursive(array_slice($arr, 0, $mid));
    $right = mergeSortRecursive(array_slice($arr, $mid));

    return mergeArrays($left, $right);
}

function mergeArrays(array $left, array $right): array
{
    $result = [];
    $i = $j = 0;

    while ($i < count($left) && $j < count($right)) {
        if ($left[$i] <= $right[$j]) {
            $result[] = $left[$i++];
        } else {
            $result[] = $right[$j++];
        }
    }

    return array_merge($result, array_slice($left, $i), array_slice($right, $j));
}

Recursion with Multiple Parameters

// Longest Common Subsequence (LCS)
function lcs(string $str1, string $str2, int $m = null, int $n = null): int
{
    $m = $m ?? strlen($str1);
    $n = $n ?? strlen($str2);

    // Base case: empty string
    if ($m === 0 || $n === 0) {
        return 0;
    }

    // If last characters match
    if ($str1[$m - 1] === $str2[$n - 1]) {
        return 1 + lcs($str1, $str2, $m - 1, $n - 1);
    }

    // If don't match, try both options
    return max(
        lcs($str1, $str2, $m - 1, $n),
        lcs($str1, $str2, $m, $n - 1)
    );
}

echo lcs("ABCDGH", "AEDFHR"); // 3 (ADH)

// With memoization for O(m×n) instead of exponential
function lcsMemo(string $str1, string $str2, int $m = null, int $n = null, array &$memo = []): int
{
    $m = $m ?? strlen($str1);
    $n = $n ?? strlen($str2);

    if ($m === 0 || $n === 0) return 0;

    $key = "{$m},{$n}";
    if (isset($memo[$key])) {
        return $memo[$key];
    }

    if ($str1[$m - 1] === $str2[$n - 1]) {
        $memo[$key] = 1 + lcsMemo($str1, $str2, $m - 1, $n - 1, $memo);
    } else {
        $memo[$key] = max(
            lcsMemo($str1, $str2, $m - 1, $n, $memo),
            lcsMemo($str1, $str2, $m, $n - 1, $memo)
        );
    }

    return $memo[$key];
}

Recursion in PHP Frameworks (~10 min)

Laravel Collections (Recursive Operations)

// Flattening nested collections
$collection = collect([
    'users' => [
        ['name' => 'John', 'posts' => [1, 2, 3]],
        ['name' => 'Jane', 'posts' => [4, 5]]
    ]
]);

// Recursive flatten
function flattenCollection($items): array
{
    $result = [];

    foreach ($items as $item) {
        if (is_array($item)) {
            $result = array_merge($result, flattenCollection($item));
        } else {
            $result[] = $item;
        }
    }

    return $result;
}

Symfony Finder (Directory Recursion)

use Symfony\Component\Finder\Finder;

// Built on recursive directory traversal
$finder = new Finder();
$finder->files()->in(__DIR__)->name('*.php');

// Manual implementation of recursive file finding
function findFiles(string $dir, string $pattern): array
{
    $result = [];
    $items = scandir($dir);

    foreach ($items as $item) {
        if ($item === '.' || $item === '..') continue;

        $path = $dir . '/' . $item;

        if (is_dir($path)) {
            // Recursive case: descend into directory
            $result = array_merge($result, findFiles($path, $pattern));
        } elseif (fnmatch($pattern, $item)) {
            // Base case: file matches pattern
            $result[] = $path;
        }
    }

    return $result;
}

Doctrine ORM (Entity Loading)

// Recursive relationship loading
class Category
{
    private $id;
    private $name;
    private $parent;
    private $children;

    // Recursively get all ancestors
    public function getAncestors(): array
    {
        if ($this->parent === null) {
            return []; // Base case: no parent
        }

        // Recursive case: parent's ancestors + parent
        return array_merge(
            $this->parent->getAncestors(),
            [$this->parent]
        );
    }

    // Recursively get all descendants
    public function getAllDescendants(): array
    {
        $descendants = [];

        foreach ($this->children as $child) {
            $descendants[] = $child;
            $descendants = array_merge(
                $descendants,
                $child->getAllDescendants()
            );
        }

        return $descendants;
    }
}

Complex Real-World Examples (~20 min)

Expression Evaluator

// Evaluate mathematical expressions recursively
interface Expression
{
    public function evaluate(): float;
}

class NumberExpr implements Expression
{
    public function __construct(private float $value) {}

    public function evaluate(): float
    {
        return $this->value;
    }
}

class BinaryExpr implements Expression
{
    public function __construct(
        private Expression $left,
        private string $operator,
        private Expression $right
    ) {}

    public function evaluate(): float
    {
        $left = $this->left->evaluate();  // Recursive
        $right = $this->right->evaluate(); // Recursive

        return match($this->operator) {
            '+' => $left + $right,
            '-' => $left - $right,
            '*' => $left * $right,
            '/' => $left / $right,
            default => throw new Exception("Unknown operator"),
        };
    }
}

// Build: (3 + 5) * (10 - 2)
$expr = new BinaryExpr(
    new BinaryExpr(new NumberExpr(3), '+', new NumberExpr(5)),
    '*',
    new BinaryExpr(new NumberExpr(10), '-', new NumberExpr(2))
);

echo $expr->evaluate(); // 64

Recursive Backtracking: Sudoku Solver

class SudokuSolver
{
    private const SIZE = 9;

    public function solve(array &$board): bool
    {
        $empty = $this->findEmpty($board);

        if ($empty === null) {
            return true; // Base case: puzzle solved
        }

        [$row, $col] = $empty;

        for ($num = 1; $num <= 9; $num++) {
            if ($this->isValid($board, $row, $col, $num)) {
                $board[$row][$col] = $num;

                // Recursive case: try to solve rest
                if ($this->solve($board)) {
                    return true;
                }

                // Backtrack
                $board[$row][$col] = 0;
            }
        }

        return false; // Trigger backtracking
    }

    private function findEmpty(array $board): ?array
    {
        for ($i = 0; $i < self::SIZE; $i++) {
            for ($j = 0; $j < self::SIZE; $j++) {
                if ($board[$i][$j] === 0) {
                    return [$i, $j];
                }
            }
        }
        return null;
    }

    private function isValid(array $board, int $row, int $col, int $num): bool
    {
        // Check row
        if (in_array($num, $board[$row])) {
            return false;
        }

        // Check column
        for ($i = 0; $i < self::SIZE; $i++) {
            if ($board[$i][$col] === $num) {
                return false;
            }
        }

        // Check 3x3 box
        $boxRow = (int)($row / 3) * 3;
        $boxCol = (int)($col / 3) * 3;

        for ($i = $boxRow; $i < $boxRow + 3; $i++) {
            for ($j = $boxCol; $j < $boxCol + 3; $j++) {
                if ($board[$i][$j] === $num) {
                    return false;
                }
            }
        }

        return true;
    }
}

Recursive Descent Parser

// Simple arithmetic parser
class Parser
{
    private array $tokens;
    private int $pos = 0;

    public function parse(string $expr): int
    {
        $this->tokens = str_split(str_replace(' ', '', $expr));
        $this->pos = 0;
        return $this->parseExpression();
    }

    private function parseExpression(): int
    {
        $result = $this->parseTerm();

        while ($this->pos < count($this->tokens) &&
               in_array($this->tokens[$this->pos], ['+', '-'])) {
            $op = $this->tokens[$this->pos++];
            $right = $this->parseTerm();
            $result = $op === '+' ? $result + $right : $result - $right;
        }

        return $result;
    }

    private function parseTerm(): int
    {
        $result = $this->parseFactor();

        while ($this->pos < count($this->tokens) &&
               in_array($this->tokens[$this->pos], ['*', '/'])) {
            $op = $this->tokens[$this->pos++];
            $right = $this->parseFactor();
            $result = $op === '*' ? $result * $right : (int)($result / $right);
        }

        return $result;
    }

    private function parseFactor(): int
    {
        if ($this->tokens[$this->pos] === '(') {
            $this->pos++; // skip '('
            $result = $this->parseExpression(); // Recursive!
            $this->pos++; // skip ')'
            return $result;
        }

        // Parse number
        $num = '';
        while ($this->pos < count($this->tokens) &&
               is_numeric($this->tokens[$this->pos])) {
            $num .= $this->tokens[$this->pos++];
        }

        return (int)$num;
    }
}

$parser = new Parser();
echo $parser->parse("3 + 5 * (2 + 3)"); // 28

Common Pitfalls and Solutions (~10 min)

Pitfall 1: Forgetting Base Case

// Wrong: Infinite recursion
function countDown(int $n): void
{
    echo "$n ";
    countDown($n - 1); // Never stops!
}

// Correct: Has base case
function countDown(int $n): void
{
    if ($n <= 0) return; // Base case
    echo "$n ";
    countDown($n - 1);
}

Pitfall 2: Not Making Progress

// Wrong: Doesn't get closer to base case
function broken(int $n): int
{
    if ($n === 0) return 0;
    return broken($n); // Same n, infinite loop!
}

// Correct: Makes progress
function working(int $n): int
{
    if ($n === 0) return 0;
    return broken($n - 1); // Moves toward base case
}

Pitfall 3: Inefficient Recursion

// Inefficient: O(2ⁿ) - recalculates same values
function fib(int $n): int
{
    if ($n <= 1) return $n;
    return fib($n - 1) + fib($n - 2);
}

// Efficient: O(n) with memoization
function fibMemo(int $n, array &$memo = []): int
{
    if ($n <= 1) return $n;
    if (isset($memo[$n])) return $memo[$n];

    $memo[$n] = fibMemo($n - 1, $memo) + fibMemo($n - 2, $memo);
    return $memo[$n];
}

// Or iterative: O(n) time, O(1) space
function fibIterative(int $n): int
{
    if ($n <= 1) return $n;

    $prev = 0;
    $curr = 1;

    for ($i = 2; $i <= $n; $i++) {
        $next = $prev + $curr;
        $prev = $curr;
        $curr = $next;
    }

    return $curr;
}

Practice Exercises (~45 min total)

::: tip Learning by Doing These exercises reinforce recursion fundamentals. Try solving each without looking at the solution first. If stuck, review the patterns from earlier sections. :::

Exercise 1: Greatest Common Divisor (GCD) (~10 min)

Use Euclid’s algorithm recursively:

function gcd(int $a, int $b): int
{
    // Your code here
}

echo gcd(48, 18); // Should output: 6

Solution

function gcd(int $a, int $b): int
{
    // Base case: if b is 0, GCD is a
    if ($b === 0) {
        return $a;
    }

    // Recursive case: GCD(a, b) = GCD(b, a % b)
    return gcd($b, $a % $b);
}

Exercise 2: Palindrome Checker (~10 min)

Check if a string is a palindrome recursively:

function isPalindrome(string $str): bool
{
    // Your code here
}

echo isPalindrome('racecar') ? 'Yes' : 'No'; // Should output: Yes

Solution

function isPalindrome(string $str): bool
{
    // Remove non-alphanumeric and convert to lowercase
    $str = strtolower(preg_replace('/[^a-z0-9]/', '', $str));

    // Base case: empty or single character
    if (strlen($str) <= 1) {
        return true;
    }

    // Check if first and last characters match
    if ($str[0] !== $str[strlen($str) - 1]) {
        return false;
    }

    // Recursive case: check middle substring
    return isPalindrome(substr($str, 1, -1));
}

Exercise 3: Flatten Nested Array (~10 min)

Flatten a multi-dimensional array into a single-level array:

function flatten(array $arr): array
{
    // Your code here
}

$nested = [1, [2, [3, 4], 5], 6];
print_r(flatten($nested)); // Should output: [1, 2, 3, 4, 5, 6]

Solution

function flatten(array $arr): array
{
    $result = [];

    foreach ($arr as $item) {
        if (is_array($item)) {
            // Recursive case: merge flattened nested array
            $result = array_merge($result, flatten($item));
        } else {
            // Base case: add single item
            $result[] = $item;
        }
    }

    return $result;
}

Exercise 4: Tower of Hanoi (~15 min)

The Tower of Hanoi is a classic recursive puzzle. Move n disks from source rod to destination rod, using an auxiliary rod, following these rules:

• Only one disk can be moved at a time
• A disk can only be placed on top of a larger disk or an empty rod
• Only the top disk can be moved

function towerOfHanoi(int $n, string $source, string $auxiliary, string $destination): void
{
    // Your code here
}

// Move 3 disks from 'A' to 'C' using 'B'
towerOfHanoi(3, 'A', 'B', 'C');

Expected output:

Move disk 1 from A to C
Move disk 2 from A to B
Move disk 1 from C to B
Move disk 3 from A to C
Move disk 1 from B to A
Move disk 2 from B to C
Move disk 1 from A to C

Solution

tower-of-hanoi.php

<?php

declare(strict_types=1);

function towerOfHanoi(int $n, string $source, string $auxiliary, string $destination): void
{
    // Base case: only 1 disk
    if ($n === 1) {
        echo "Move disk 1 from {$source} to {$destination}\n";
        return;
    }

    // Step 1: Move n-1 disks from source to auxiliary (using destination)
    towerOfHanoi($n - 1, $source, $destination, $auxiliary);

    // Step 2: Move largest disk from source to destination
    echo "Move disk {$n} from {$source} to {$destination}\n";

    // Step 3: Move n-1 disks from auxiliary to destination (using source)
    towerOfHanoi($n - 1, $auxiliary, $source, $destination);
}

// Test with 3 disks
echo "Solution for 3 disks:\n";
towerOfHanoi(3, 'A', 'B', 'C');

echo "\nTotal moves for n disks: 2^n - 1\n";
echo "For 3 disks: 2^3 - 1 = 7 moves\n";

Why it works:

The Tower of Hanoi perfectly demonstrates recursive problem-solving:

1. Base case: If n=1, simply move the disk
2. Recursive case:
   • Move n-1 disks out of the way (to auxiliary)
   • Move the largest disk to destination
   • Move the n-1 disks from auxiliary to destination

Time complexity: O(2ⁿ) - each disk doubles the moves

• 1 disk: 1 move
• 2 disks: 3 moves
• 3 disks: 7 moves
• 4 disks: 15 moves
• n disks: 2ⁿ - 1 moves

Space complexity: O(n) - recursion depth equals number of disks

Wrap-up

Congratulations! You’ve mastered recursion fundamentals—one of the most powerful problem-solving techniques in programming. Here’s what you’ve accomplished:

• ✓ Understood recursive thinking and how functions can call themselves to solve problems
• ✓ Mastered the two essential parts of recursion: base case (stopping condition) and recursive case (progress toward solution)
• ✓ Learned how the call stack works and how PHP manages recursive function calls
• ✓ Implemented classic recursive algorithms including factorial, Fibonacci, and array operations
• ✓ Optimized recursive functions using memoization (transforming O(2ⁿ) to O(n))
• ✓ Applied recursion to real-world problems including file system traversal, JSON validation, menu rendering, and backtracking
• ✓ Built complex recursive solutions including Sudoku solver, recursive descent parser, and Tower of Hanoi
• ✓ Learned production-safe recursion with depth tracking, error handling, and memory management
• ✓ Learned when to use recursion vs iteration based on clarity, performance, and stack depth considerations
• ✓ Avoided common pitfalls including infinite recursion, stack overflow, and inefficient implementations
• ✓ Measured recursion limits and implemented safe recursion patterns for production code

Key Takeaways

• Recursion is when a function calls itself to solve smaller subproblems
• Every recursive function needs a base case (stopping condition) and recursive case (progress toward base)
• The call stack tracks recursive calls; too many can cause stack overflow (PHP limit: ~100-512 levels)
• Memoization can dramatically improve recursive performance (O(2ⁿ) → O(n) for Fibonacci)
• Many recursive problems can be solved iteratively—choose based on clarity and performance
• Recursion shines with naturally recursive data structures (trees, nested data, file systems)
• Always make progress toward the base case to avoid infinite recursion
• Consider stack depth limits for production code with large datasets
• Recursion uses O(n) stack space vs iteration’s O(1)—memory matters for large n
• Implement recursion depth tracking and error handling for production safety
• Measure your system’s recursion limits before deployment

You now have the foundation to tackle complex recursive algorithms. In the next chapter, we’ll explore problem-solving strategies that combine recursion with techniques like divide-and-conquer, backtracking, and dynamic programming.

Further Reading

Deepen your understanding with these resources:

• PHP Functions Documentation — Official PHP documentation on user-defined functions
• Call Stack on Wikipedia — Deep dive into how the call stack works in programming languages
• Tail Call Optimization — Understanding tail recursion and why some languages optimize it
• Dynamic Programming Overview — Where memoization fits into the bigger picture of algorithmic optimization
• Recursion Visualizer — Interactive tool to visualize recursive function calls
• Master Theorem — Mathematical framework for analyzing divide-and-conquer recursive algorithms
• Backtracking Algorithms — Problem-solving technique that uses recursion to explore all possibilities

What’s Next

In the next chapter, we’ll explore Problem-Solving Strategies that combine recursion with other techniques like divide-and-conquer, backtracking, and dynamic programming.

💻 Code Samples

All code examples from this chapter are available in the GitHub repository:

View Chapter 03 Code Samples

Files included:

• 01-recursion-basics.php - Complete recursion examples including basic recursion, Fibonacci (naive, memoized, iterative), recursive data structures, divide and conquer, and backtracking
• README.md - Complete documentation and usage guide

Clone the repository to run the examples locally:

git clone https://github.com/dalehurley/codewithphp.git
cd codewithphp/code/php-algorithms/chapter-03
php 01-recursion-basics.php

---

Continue to Chapter 04: Problem-Solving Strategies.