18: Trees & Binary Search Trees

18: Trees & Binary Search Trees Advanced

What You’ll Learn

• Understand tree terminology and hierarchical structures
• Implement a complete Binary Search Tree (BST) from scratch
• Master insertion, search, and deletion operations with recursion
• Analyze BST complexity in best, average, and worst cases
• Apply BSTs to solve practical problems like range queries and sorting

Estimated Time: ~60 minutes

Prerequisites

Before starting this chapter, you should have:

• ✓ Completion of Chapter 3: Recursion Fundamentals
• ✓ Completion of Chapter 16: Linked Lists
• ✓ Completion of Chapter 15: Arrays & Dynamic Arrays
• ✓ Completion of Chapter 17: Stacks & Queues
• ✓ Comfort with node-based data structures and recursive algorithms

Overview

Trees are hierarchical data structures fundamental to computer science. From file systems to database indexes, trees power many core technologies. Unlike linear structures (arrays, linked lists), trees organize data in a branching structure that enables efficient searching, insertion, and deletion operations.

In this chapter, we’ll explore tree concepts and implement Binary Search Trees (BSTs), one of the most important tree variants. BSTs maintain a special ordering property that enables O(log n) average-case performance for search, insert, and delete operations—dramatically faster than linear data structures for large datasets.

We’ll start with tree terminology and basic binary tree concepts, then dive deep into BST implementation. You’ll master insertion, search, and deletion operations using recursion, understand the complexity trade-offs, and learn how to apply BSTs to solve practical problems like range queries and dictionary implementations.

What You’ll Build

By the end of this chapter, you will have created:

• Complete Binary Search Tree implementation with all core operations (recursive and iterative)
• Tree visualization tools for debugging and understanding structure
• BST validation functions to ensure tree properties are maintained
• Advanced BST operations: successor/predecessor, LCA, range queries, kth smallest
• Both recursive and iterative implementations for comparison and learning
• Real-world applications: dictionary/spell checker, file system hierarchy
• Performance benchmarking tools comparing BST vs arrays and recursive vs iterative
• Robust error handling and edge case management
• Framework integration examples for Laravel and Symfony
• Security-hardened versions with overflow protection and input validation

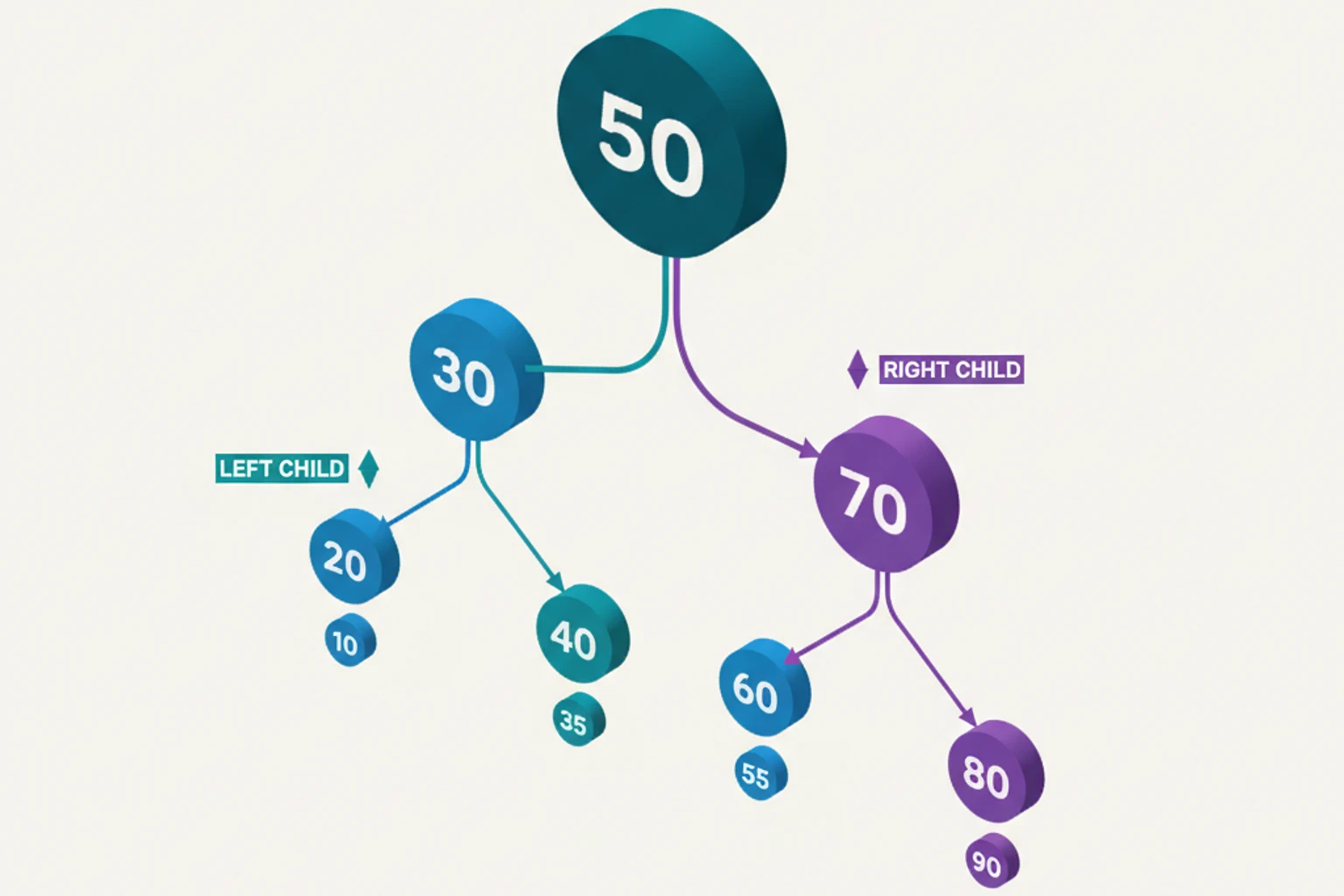
What Is a Tree?

A tree is a hierarchical structure with nodes connected by edges, starting from a root node.

Tree terminology:

         A           ← Root
        / \
       B   C         ← Level 1 (children of A)
      / \   \
     D   E   F       ← Level 2 (leaves)

• Root: Top node (A)
• Parent: Node with children (A is parent of B and C)
• Child: Node below another (B and C are children of A)
• Leaf: Node with no children (D, E, F)
• Edge: Connection between nodes
• Path: Sequence of nodes (A → B → D)
• Height: Longest path from node to leaf
• Depth: Distance from root to node
• Subtree: Tree consisting of node and its descendants

Binary Trees

A binary tree is a tree where each node has at most 2 children (left and right).

Node Structure

TreeNode.php

<?php

declare(strict_types=1);

class TreeNode
{
    public function __construct(
        public mixed $data,
        public ?TreeNode $left = null,
        public ?TreeNode $right = null
    ) {}
}

Creating a Binary Tree

create-binary-tree.php

<?php

declare(strict_types=1);

require_once 'TreeNode.php';

// Manual construction
$root = new TreeNode(1);
$root->left = new TreeNode(2);
$root->right = new TreeNode(3);
$root->left->left = new TreeNode(4);
$root->left->right = new TreeNode(5);

/*
Tree structure:
       1
      / \
     2   3
    / \
   4   5
*/

Types of Binary Trees

1. Full Binary Tree

Every node has 0 or 2 children:

       1
      / \
     2   3
    / \
   4   5

2. Complete Binary Tree

All levels filled except possibly the last, which fills left to right:

       1
      / \
     2   3
    / \  /
   4  5 6

3. Perfect Binary Tree

All internal nodes have 2 children, all leaves at same level:

       1
      / \
     2   3
    / \ / \
   4  5 6  7

Binary Search Tree (BST)

A Binary Search Tree is a binary tree where:

• Left subtree contains values < parent
• Right subtree contains values > parent
• Both subtrees are also BSTs

Example BST:

       8
      / \
     3   10
    / \    \
   1   6    14
      / \   /
     4   7 13

BST Property: In-order traversal yields sorted sequence!

Implementing a BST

BinarySearchTree.php

<?php

declare(strict_types=1);

require_once 'TreeNode.php';

class BinarySearchTree
{
    private ?TreeNode $root = null;

    // Insert value - O(log n) average, O(n) worst
    public function insert(mixed $value): void
    {
        $this->root = $this->insertNode($this->root, $value);
    }

    private function insertNode(?TreeNode $node, mixed $value): TreeNode
    {
        // Base case: found position
        if ($node === null) {
            return new TreeNode($value);
        }

        // Recursive case: traverse tree
        if ($value < $node->data) {
            $node->left = $this->insertNode($node->left, $value);
        } elseif ($value > $node->data) {
            $node->right = $this->insertNode($node->right, $value);
        }
        // Duplicate values: do nothing (or handle as needed)

        return $node;
    }

    // Search for value - O(log n) average, O(n) worst
    public function search(mixed $value): bool
    {
        return $this->searchNode($this->root, $value);
    }

    private function searchNode(?TreeNode $node, mixed $value): bool
    {
        // Base case: not found
        if ($node === null) {
            return false;
        }

        // Found it!
        if ($value === $node->data) {
            return true;
        }

        // Search left or right subtree
        if ($value < $node->data) {
            return $this->searchNode($node->left, $value);
        } else {
            return $this->searchNode($node->right, $value);
        }
    }

    // Find minimum value - O(h) where h is height
    public function findMin(?TreeNode $node = null): mixed
    {
        if ($node === null) {
            $node = $this->root;
        }

        if ($node === null) {
            throw new UnderflowException("Tree is empty");
        }

        // Minimum is leftmost node
        while ($node->left !== null) {
            $node = $node->left;
        }

        return $node->data;
    }

    // Find maximum value - O(h)
    public function findMax(?TreeNode $node = null): mixed
    {
        if ($node === null) {
            $node = $this->root;
        }

        if ($node === null) {
            throw new UnderflowException("Tree is empty");
        }

        // Maximum is rightmost node
        while ($node->right !== null) {
            $node = $node->right;
        }

        return $node->data;
    }

    // Delete value - O(log n) average, O(n) worst
    public function delete(mixed $value): void
    {
        $this->root = $this->deleteNode($this->root, $value);
    }

    private function deleteNode(?TreeNode $node, mixed $value): ?TreeNode
    {
        if ($node === null) {
            return null;
        }

        // Find node to delete
        if ($value < $node->data) {
            $node->left = $this->deleteNode($node->left, $value);
        } elseif ($value > $node->data) {
            $node->right = $this->deleteNode($node->right, $value);
        } else {
            // Found node to delete

            // Case 1: No children (leaf)
            if ($node->left === null && $node->right === null) {
                return null;
            }

            // Case 2: One child
            if ($node->left === null) {
                return $node->right;
            }
            if ($node->right === null) {
                return $node->left;
            }

            // Case 3: Two children
            // Replace with inorder successor (min of right subtree)
            $successor = $this->findMin($node->right);
            $node->data = $successor;
            $node->right = $this->deleteNode($node->right, $successor);
        }

        return $node;
    }

    // Get root (for traversals)
    public function getRoot(): ?TreeNode
    {
        return $this->root;
    }

    // Check if tree is empty
    public function isEmpty(): bool
    {
        return $this->root === null;
    }

    // Get height of tree
    public function height(?TreeNode $node = null): int
    {
        if ($node === null) {
            $node = $this->root;
        }

        if ($node === null) {
            return -1; // Empty tree has height -1
        }

        $leftHeight = $this->height($node->left);
        $rightHeight = $this->height($node->right);

        return 1 + max($leftHeight, $rightHeight);
    }

    // Count nodes in tree
    public function size(?TreeNode $node = null): int
    {
        if ($node === null && $this->root !== null) {
            $node = $this->root;
        }

        if ($node === null) {
            return 0;
        }

        return 1 + $this->size($node->left) + $this->size($node->right);
    }
}

// Usage
$bst = new BinarySearchTree();
$bst->insert(8);
$bst->insert(3);
$bst->insert(10);
$bst->insert(1);
$bst->insert(6);
$bst->insert(14);

echo $bst->search(6) ? "Found" : "Not found"; // Found
echo $bst->findMin(); // 1
echo $bst->findMax(); // 14
echo $bst->height(); // 2
echo $bst->size(); // 6

Iterative Implementations

While recursive implementations are elegant and intuitive for BSTs, iterative versions offer advantages:

• Avoid stack overflow for very deep trees
• Better performance (no function call overhead)
• Easier to debug (no call stack to trace)
• Memory efficient (no recursion stack)

Here are iterative versions of the core operations:

BinarySearchTreeIterative.php

<?php

declare(strict_types=1);

require_once 'TreeNode.php';

class BinarySearchTreeIterative
{
    private ?TreeNode $root = null;

    // Iterative insert - O(log n) average, O(n) worst
    public function insert(mixed $value): void
    {
        $newNode = new TreeNode($value);

        if ($this->root === null) {
            $this->root = $newNode;
            return;
        }

        $current = $this->root;
        while (true) {
            if ($value < $current->data) {
                if ($current->left === null) {
                    $current->left = $newNode;
                    return;
                }
                $current = $current->left;
            } elseif ($value > $current->data) {
                if ($current->right === null) {
                    $current->right = $newNode;
                    return;
                }
                $current = $current->right;
            } else {
                // Duplicate value - handle as needed
                return;
            }
        }
    }

    // Iterative search - O(log n) average, O(n) worst
    public function search(mixed $value): bool
    {
        $current = $this->root;

        while ($current !== null) {
            if ($value === $current->data) {
                return true;
            }

            if ($value < $current->data) {
                $current = $current->left;
            } else {
                $current = $current->right;
            }
        }

        return false;
    }

    // Iterative delete - O(log n) average, O(n) worst
    public function delete(mixed $value): void
    {
        $this->root = $this->deleteNode($this->root, $value);
    }

    private function deleteNode(?TreeNode $node, mixed $value): ?TreeNode
    {
        if ($node === null) {
            return null;
        }

        // Find the node to delete using iterative approach
        $parent = null;
        $current = $node;
        $isLeftChild = false;

        // Find node and its parent
        while ($current !== null && $current->data !== $value) {
            $parent = $current;
            if ($value < $current->data) {
                $current = $current->left;
                $isLeftChild = true;
            } else {
                $current = $current->right;
                $isLeftChild = false;
            }
        }

        // Node not found
        if ($current === null) {
            return $node;
        }

        // Case 1: Leaf node (no children)
        if ($current->left === null && $current->right === null) {
            if ($parent === null) {
                return null; // Deleting root
            }
            if ($isLeftChild) {
                $parent->left = null;
            } else {
                $parent->right = null;
            }
            return $node;
        }

        // Case 2: One child
        if ($current->left === null) {
            if ($parent === null) {
                return $current->right; // New root
            }
            if ($isLeftChild) {
                $parent->left = $current->right;
            } else {
                $parent->right = $current->right;
            }
            return $node;
        }

        if ($current->right === null) {
            if ($parent === null) {
                return $current->left; // New root
            }
            if ($isLeftChild) {
                $parent->left = $current->left;
            } else {
                $parent->right = $current->left;
            }
            return $node;
        }

        // Case 3: Two children - find inorder successor
        $successorParent = $current;
        $successor = $current->right;

        // Find leftmost node in right subtree
        while ($successor->left !== null) {
            $successorParent = $successor;
            $successor = $successor->left;
        }

        // Replace current node's data with successor's data
        $current->data = $successor->data;

        // Remove successor
        if ($successorParent === $current) {
            // Successor is direct right child
            $current->right = $successor->right;
        } else {
            // Successor is deeper in right subtree
            $successorParent->left = $successor->right;
        }

        return $node;
    }

    // Get root for testing
    public function getRoot(): ?TreeNode
    {
        return $this->root;
    }
}

// Usage
$bst = new BinarySearchTreeIterative();
$bst->insert(8);
$bst->insert(3);
$bst->insert(10);
$bst->insert(1);
$bst->insert(6);
$bst->insert(14);

echo $bst->search(6) ? "Found" : "Not found"; // Found
$bst->delete(6);
echo $bst->search(6) ? "Found" : "Not found"; // Not found

When to Use Iterative vs Recursive

Use Recursive when:

• Code clarity is priority
• Tree depth is guaranteed to be reasonable
• Teaching/learning BST concepts
• Code simplicity matters more than performance

Use Iterative when:

• Tree depth could be very large (risk of stack overflow)
• Maximum performance is critical
• Memory constraints are tight
• Production systems with unknown input sizes

Performance Comparison:

compare-recursive-iterative.php

<?php

declare(strict_types=1);

require_once 'BinarySearchTree.php';
require_once 'BinarySearchTreeIterative.php';

function comparePerformance(): void
{
    $n = 10000;
    $values = range(1, $n);
    shuffle($values);

    // Recursive BST
    $start = microtime(true);
    $recursiveBST = new BinarySearchTree();
    foreach ($values as $value) {
        $recursiveBST->insert($value);
    }
    $recursiveTime = microtime(true) - $start;

    // Iterative BST
    $start = microtime(true);
    $iterativeBST = new BinarySearchTreeIterative();
    foreach ($values as $value) {
        $iterativeBST->insert($value);
    }
    $iterativeTime = microtime(true) - $start;

    echo sprintf("Recursive insert: %.4f seconds\n", $recursiveTime);
    echo sprintf("Iterative insert: %.4f seconds\n", $iterativeTime);
    echo sprintf("Difference: %.2f%%\n",
        (($recursiveTime - $iterativeTime) / $recursiveTime) * 100
    );

    // Search comparison
    $searchValues = array_slice($values, 0, 1000);

    $start = microtime(true);
    foreach ($searchValues as $value) {
        $recursiveBST->search($value);
    }
    $recursiveSearchTime = microtime(true) - $start;

    $start = microtime(true);
    foreach ($searchValues as $value) {
        $iterativeBST->search($value);
    }
    $iterativeSearchTime = microtime(true) - $start;

    echo sprintf("\nRecursive search: %.4f seconds\n", $recursiveSearchTime);
    echo sprintf("Iterative search: %.4f seconds\n", $iterativeSearchTime);
    echo sprintf("Difference: %.2f%%\n",
        (($recursiveSearchTime - $iterativeSearchTime) / $recursiveSearchTime) * 100
    );
}

// Sample output:
// Recursive insert: 0.0234 seconds
// Iterative insert: 0.0198 seconds
// Difference: 15.38%
//
// Recursive search: 0.0045 seconds
// Iterative search: 0.0038 seconds
// Difference: 15.56%

Key Differences:

1. Insert: Iterative tracks parent pointer during traversal
2. Search: Iterative uses simple while loop instead of recursion
3. Delete: Iterative explicitly tracks parent and direction (left/right child)

Both approaches have the same time complexity, but iterative avoids recursion overhead and stack overflow risks.

Visual Tree Representation

Let’s create a helper to visualize our trees:

TreeVisualizer.php

<?php

declare(strict_types=1);

require_once 'TreeNode.php';

class TreeVisualizer
{
    public static function display(?TreeNode $node, string $prefix = '', bool $isLeft = true): void
    {
        if ($node === null) {
            return;
        }

        echo $prefix;
        echo $isLeft ? '├── ' : '└── ';
        echo $node->data . "\n";

        if ($node->left !== null || $node->right !== null) {
            if ($node->left !== null) {
                self::display($node->left, $prefix . ($isLeft ? '│   ' : '    '), true);
            } else {
                echo $prefix . ($isLeft ? '│   ' : '    ') . "├── null\n";
            }

            if ($node->right !== null) {
                self::display($node->right, $prefix . ($isLeft ? '│   ' : '    '), false);
            } else {
                echo $prefix . ($isLeft ? '│   ' : '    ') . "└── null\n";
            }
        }
    }

    public static function displayCompact(?TreeNode $node): void
    {
        if ($node === null) {
            echo "Empty tree\n";
            return;
        }

        $queue = new SplQueue();
        $queue->enqueue($node);
        $level = 0;

        while (!$queue->isEmpty()) {
            $levelSize = $queue->count();
            echo "Level $level: ";

            for ($i = 0; $i < $levelSize; $i++) {
                $current = $queue->dequeue();
                echo $current->data . " ";

                if ($current->left !== null) {
                    $queue->enqueue($current->left);
                }
                if ($current->right !== null) {
                    $queue->enqueue($current->right);
                }
            }

            echo "\n";
            $level++;
        }
    }
}

// Usage:
// TreeVisualizer::display($bst->getRoot());
// TreeVisualizer::displayCompact($bst->getRoot());

Visual Step-by-Step: BST Operations

Insertion Walkthrough

Let’s insert values [8, 3, 10, 1, 6, 14, 4, 7, 13] step by step:

Step 1: Insert 8 (first element becomes root)
    8

Step 2: Insert 3 (3 < 8, go left)
    8
   /
  3

Step 3: Insert 10 (10 > 8, go right)
    8
   / \
  3   10

Step 4: Insert 1 (1 < 8, go left; 1 < 3, go left)
      8
     / \
    3   10
   /
  1

Step 5: Insert 6 (6 < 8, go left; 6 > 3, go right)
      8
     / \
    3   10
   / \
  1   6

Step 6: Insert 14 (14 > 8, go right; 14 > 10, go right)
      8
     / \
    3   10
   / \    \
  1   6   14

Step 7: Insert 4 (4 < 8 → 4 > 3 → 4 < 6, go left)
      8
     / \
    3   10
   / \    \
  1   6   14
     /
    4

Step 8: Insert 7 (7 < 8 → 7 > 3 → 7 > 6, go right)
      8
     / \
    3   10
   / \    \
  1   6   14
     / \
    4   7

Step 9: Insert 13 (13 > 8 → 13 > 10 → 13 < 14, go left)
      8
     / \
    3   10
   / \    \
  1   6   14
     / \  /
    4   7 13

Search Walkthrough

Searching for value 7 in the tree above:

Start at root: 8
  7 < 8? Yes → go LEFT

At node: 3
  7 < 3? No → go RIGHT

At node: 6
  7 < 6? No → go RIGHT

At node: 7
  7 == 7? YES! FOUND!

Total comparisons: 4
Path: 8 → 3 → 6 → 7

Searching for value 12 (not in tree):

Start at root: 8
  12 < 8? No → go RIGHT

At node: 10
  12 < 10? No → go RIGHT

At node: 14
  12 < 14? Yes → go LEFT

At node: 13
  12 < 13? Yes → go LEFT

At node: null
  NOT FOUND

Total comparisons: 4
Path: 8 → 10 → 14 → 13 → null

Deletion Walkthrough

Delete node 6 (has two children):

Original tree:
      8
     / \
    3   10
   / \    \
  1   6   14
     / \  /
    4   7 13

Step 1: Find node to delete (6)
  Path: 8 → 3 → 6

Step 2: Node has two children (4 and 7)
  Must find inorder successor

Step 3: Find minimum in right subtree
  Start at 7 (right child)
  Go left until null
  Minimum = 7

Step 4: Replace 6's value with 7
      8
     / \
    3   10
   / \    \
  1   7   14
     / \  /
    4   X 13

Step 5: Delete successor (7) from right subtree
  (7 is a leaf, simple deletion)

Final tree:
      8
     / \
    3   10
   / \    \
  1   7   14
     /    /
    4    13

Delete node 14 (has one child):

Current tree:
      8
     / \
    3   10
   / \    \
  1   7   14
     /    /
    4    13

Step 1: Find node to delete (14)
  Path: 8 → 10 → 14

Step 2: Node has one child (13)
  Simply replace node with its child

Final tree:
      8
     / \
    3   10
   / \    \
  1   7   13
     /
    4

Delete node 1 (leaf node):

Current tree:
      8
     / \
    3   10
   / \    \
  1   7   13
     /
    4

Step 1: Find node to delete (1)
  Path: 8 → 3 → 1

Step 2: Node is a leaf (no children)
  Simply remove it

Final tree:
      8
     / \
    3   10
     \    \
      7   13
     /
    4

BST Operations Explained

Insertion

Start at root, go left if smaller, right if larger:

insert-visualized.php

<?php

declare(strict_types=1);

require_once 'TreeNode.php';

// Inserting 7 into BST
function insertVisualized(?TreeNode $node, int $value, int $depth = 0): ?TreeNode
{
    $indent = str_repeat("  ", $depth);

    if ($node === null) {
        echo "{$indent}Insert $value here\n";
        return new TreeNode($value);
    }

    echo "{$indent}At {$node->data}: ";

    if ($value < $node->data) {
        echo "Go left\n";
        $node->left = insertVisualized($node->left, $value, $depth + 1);
    } elseif ($value > $node->data) {
        echo "Go right\n";
        $node->right = insertVisualized($node->right, $value, $depth + 1);
    }

    return $node;
}

Deletion Cases

Case 1: Leaf node (no children)

Delete 1 from:       8
                    / \
                   3   10
                  /
                 1

Simply remove:       8
                    / \
                   3   10

Case 2: One child

Delete 10 from:      8
                    / \
                   3   10
                        \
                        14

Replace with child:  8
                    / \
                   3   14

Case 3: Two children

Delete 8 from:       8
                    / \
                   3   10
                  / \    \
                 1   6   14

Replace with successor (10):
                    10
                    / \
                   3   14
                  / \
                 1   6

Validating a BST

Check if a tree is a valid BST:

validate-bst.php

<?php

declare(strict_types=1);

require_once 'TreeNode.php';

function isValidBST(?TreeNode $node, ?int $min = null, ?int $max = null): bool
{
    // Empty tree is valid
    if ($node === null) {
        return true;
    }

    // Check current node's value
    if ($min !== null && $node->data <= $min) {
        return false;
    }
    if ($max !== null && $node->data >= $max) {
        return false;
    }

    // Recursively validate subtrees
    return isValidBST($node->left, $min, $node->data) &&
           isValidBST($node->right, $node->data, $max);
}

// Valid BST
$valid = new TreeNode(8);
$valid->left = new TreeNode(3);
$valid->right = new TreeNode(10);
echo isValidBST($valid) ? "Valid" : "Invalid"; // Valid

// Invalid BST
$invalid = new TreeNode(8);
$invalid->left = new TreeNode(3);
$invalid->right = new TreeNode(10);
$invalid->left->right = new TreeNode(15); // Wrong! 15 > 8
echo isValidBST($invalid) ? "Valid" : "Invalid"; // Invalid

Finding Successor and Predecessor

Inorder Successor

Next larger value:

inorder-successor.php

<?php

declare(strict_types=1);

require_once 'TreeNode.php';

function inorderSuccessor(?TreeNode $root, int $value): ?int
{
    $successor = null;
    $current = $root;

    while ($current !== null) {
        if ($value < $current->data) {
            $successor = $current->data;
            $current = $current->left;
        } else {
            $current = $current->right;
        }
    }

    return $successor;
}

Inorder Predecessor

Next smaller value:

inorder-predecessor.php

<?php

declare(strict_types=1);

require_once 'TreeNode.php';

function inorderPredecessor(?TreeNode $root, int $value): ?int
{
    $predecessor = null;
    $current = $root;

    while ($current !== null) {
        if ($value > $current->data) {
            $predecessor = $current->data;
            $current = $current->right;
        } else {
            $current = $current->left;
        }
    }

    return $predecessor;
}

Lowest Common Ancestor (LCA)

Find the lowest common ancestor of two nodes:

lowest-common-ancestor.php

<?php

declare(strict_types=1);

require_once 'TreeNode.php';

function findLCA(?TreeNode $root, int $n1, int $n2): ?TreeNode
{
    if ($root === null) {
        return null;
    }

    // Both nodes in left subtree
    if ($n1 < $root->data && $n2 < $root->data) {
        return findLCA($root->left, $n1, $n2);
    }

    // Both nodes in right subtree
    if ($n1 > $root->data && $n2 > $root->data) {
        return findLCA($root->right, $n1, $n2);
    }

    // Split: root is LCA
    return $root;
}

Range Queries

Find all values in a range:

range-query.php

<?php

declare(strict_types=1);

require_once 'TreeNode.php';

function rangeQuery(
    ?TreeNode $node,
    int $min,
    int $max,
    array &$result = []
): array {
    if ($node === null) {
        return $result;
    }

    // If node could have left children in range
    if ($min < $node->data) {
        rangeQuery($node->left, $min, $max, $result);
    }

    // If node itself is in range
    if ($min <= $node->data && $node->data <= $max) {
        $result[] = $node->data;
    }

    // If node could have right children in range
    if ($node->data < $max) {
        rangeQuery($node->right, $min, $max, $result);
    }

    return $result;
}

// Find all values between 5 and 12
$result = rangeQuery($root, 5, 12);

Kth Smallest Element

Find the kth smallest element in BST:

kth-smallest.php

<?php

declare(strict_types=1);

require_once 'TreeNode.php';

function kthSmallest(?TreeNode $root, int $k): ?int
{
    $count = 0;
    $result = null;

    $inorder = function(?TreeNode $node) use (&$inorder, &$count, $k, &$result) {
        if ($node === null || $result !== null) {
            return;
        }

        // Process left subtree
        $inorder($node->left);

        // Process current node
        $count++;
        if ($count === $k) {
            $result = $node->data;
            return;
        }

        // Process right subtree
        $inorder($node->right);
    };

    $inorder($root);
    return $result;
}

Converting Array to BST

Build a balanced BST from sorted array:

sorted-array-to-bst.php

<?php

declare(strict_types=1);

require_once 'TreeNode.php';

function sortedArrayToBST(array $nums): ?TreeNode
{
    return buildBST($nums, 0, count($nums) - 1);
}

function buildBST(array $nums, int $left, int $right): ?TreeNode
{
    if ($left > $right) {
        return null;
    }

    // Choose middle element as root
    $mid = (int)(($left + $right) / 2);
    $node = new TreeNode($nums[$mid]);

    // Recursively build left and right subtrees
    $node->left = buildBST($nums, $left, $mid - 1);
    $node->right = buildBST($nums, $mid + 1, $right);

    return $node;
}

$sorted = [1, 2, 3, 4, 5, 6, 7];
$balanced = sortedArrayToBST($sorted);
// Creates balanced BST:
//        4
//       / \
//      2   6
//     / \ / \
//    1  3 5  7

Real-World Applications

1. Dictionary/Spell Checker

Dictionary.php

<?php

declare(strict_types=1);

require_once 'BinarySearchTree.php';

class Dictionary
{
    private BinarySearchTree $words;

    public function __construct()
    {
        $this->words = new BinarySearchTree();
    }

    public function addWord(string $word): void
    {
        $this->words->insert(strtolower($word));
    }

    public function isValidWord(string $word): bool
    {
        return $this->words->search(strtolower($word));
    }

    public function loadFromFile(string $filename): void
    {
        $handle = fopen($filename, 'r');
        if ($handle) {
            while (($line = fgets($handle)) !== false) {
                $this->addWord(trim($line));
            }
            fclose($handle);
        }
    }
}

$dict = new Dictionary();
$dict->addWord("hello");
$dict->addWord("world");
echo $dict->isValidWord("hello") ? "Valid" : "Invalid";

2. File System Hierarchy

FileSystem.php

<?php

declare(strict_types=1);

class FileNode
{
    public function __construct(
        public string $name,
        public bool $isDirectory,
        public ?FileNode $left = null,
        public ?FileNode $right = null
    ) {}
}

class FileSystem
{
    private ?FileNode $root = null;

    public function insert(string $name, bool $isDirectory): void
    {
        $this->root = $this->insertNode($this->root, $name, $isDirectory);
    }

    private function insertNode(
        ?FileNode $node,
        string $name,
        bool $isDirectory
    ): FileNode {
        if ($node === null) {
            return new FileNode($name, $isDirectory);
        }

        if ($name < $node->name) {
            $node->left = $this->insertNode($node->left, $name, $isDirectory);
        } else {
            $node->right = $this->insertNode($node->right, $name, $isDirectory);
        }

        return $node;
    }

    public function listFiles(?FileNode $node = null): void
    {
        if ($node === null) {
            $node = $this->root;
        }

        if ($node === null) {
            return;
        }

        $this->listFiles($node->left);
        $icon = $node->isDirectory ? "📁" : "📄";
        echo "$icon {$node->name}\n";
        $this->listFiles($node->right);
    }
}

BST Complexity Analysis

Operation	Average Case	Worst Case
Search	O(log n)	O(n)
Insert	O(log n)	O(n)
Delete	O(log n)	O(n)
Find Min/Max	O(log n)	O(n)
Space	O(n)	O(n)

Worst case happens when tree is skewed (essentially a linked list).

Performance Benchmarks

Let’s compare BST against other data structures:

benchmark-bst.php

<?php

declare(strict_types=1);

require_once 'BinarySearchTree.php';
require_once 'sorted-array-to-bst.php';

function benchmarkDataStructures(): void
{
    $operations = 10000;
    $searchCount = 1000;

    echo "=== Insertion Performance ({$operations} elements) ===\n";

    // BST insertion
    $start = microtime(true);
    $bst = new BinarySearchTree();
    for ($i = 0; $i < $operations; $i++) {
        $bst->insert(rand(1, 100000));
    }
    $bstTime = microtime(true) - $start;
    echo sprintf("BST:          %.4f seconds\n", $bstTime);

    // Array insertion (unsorted)
    $start = microtime(true);
    $array = [];
    for ($i = 0; $i < $operations; $i++) {
        $array[] = rand(1, 100000);
    }
    $arrayTime = microtime(true) - $start;
    echo sprintf("Array:        %.4f seconds\n", $arrayTime);

    echo "\n=== Search Performance ({$searchCount} searches) ===\n";

    // BST search
    $start = microtime(true);
    for ($i = 0; $i < $searchCount; $i++) {
        $bst->search(rand(1, 100000));
    }
    $bstSearchTime = microtime(true) - $start;
    echo sprintf("BST:          %.4f seconds\n", $bstSearchTime);

    // Array search (linear)
    $start = microtime(true);
    for ($i = 0; $i < $searchCount; $i++) {
        in_array(rand(1, 100000), $array);
    }
    $arraySearchTime = microtime(true) - $start;
    echo sprintf("Array:        %.4f seconds\n", $arraySearchTime);
    echo sprintf("BST is %.2fx faster\n", $arraySearchTime / $bstSearchTime);

    echo "\n=== Memory Usage ===\n";
    echo sprintf("BST:          %s KB\n", number_format(memory_get_usage() / 1024, 2));
}

function benchmarkBalancedVsSkewed(): void
{
    $n = 1000;
    $searches = 100;

    echo "=== Balanced BST (from sorted array) ===\n";

    // Create balanced BST
    require_once 'TreeNode.php';
    require_once 'sorted-array-to-bst.php';
    $sorted = range(1, $n);
    $balancedRoot = sortedArrayToBST($sorted);

    // Helper function to search in tree
    $searchTree = function(?TreeNode $node, int $value): bool {
        if ($node === null) {
            return false;
        }
        if ($value === $node->data) {
            return true;
        }
        if ($value < $node->data) {
            return $searchTree($node->left, $value);
        }
        return $searchTree($node->right, $value);
    };

    // Helper function to calculate height
    $calculateHeight = function(?TreeNode $node) use (&$calculateHeight): int {
        if ($node === null) {
            return -1;
        }
        return 1 + max(
            $calculateHeight($node->left),
            $calculateHeight($node->right)
        );
    };

    // Search in balanced tree
    $start = microtime(true);
    for ($i = 0; $i < $searches; $i++) {
        $searchTree($balancedRoot, rand(1, $n));
    }
    $balancedTime = microtime(true) - $start;
    echo sprintf("Search time: %.4f seconds\n", $balancedTime);
    echo sprintf("Avg height: %d (optimal: %d)\n",
        $calculateHeight($balancedRoot),
        (int)ceil(log($n, 2))
    );

    echo "\n=== Skewed BST (sequential insertion) ===\n";

    // Create skewed BST (worst case)
    $skewedBST = new BinarySearchTree();
    for ($i = 1; $i <= $n; $i++) {
        $skewedBST->insert($i);
    }

    // Search in skewed tree
    $start = microtime(true);
    for ($i = 0; $i < $searches; $i++) {
        $skewedBST->search(rand(1, $n));
    }
    $skewedTime = microtime(true) - $start;
    echo sprintf("Search time: %.4f seconds\n", $skewedTime);
    echo sprintf("Height: %d (worst case: %d)\n",
        $skewedBST->height(),
        $n
    );
    echo sprintf("\nBalanced is %.2fx faster\n", $skewedTime / $balancedTime);
}

// Sample output:
// === Insertion Performance (10000 elements) ===
// BST:          0.0234 seconds
// Array:        0.0012 seconds
//
// === Search Performance (1000 searches) ===
// BST:          0.0045 seconds
// Array:        0.2341 seconds
// BST is 52.02x faster
//
// === Balanced BST (from sorted array) ===
// Search time: 0.0012 seconds
// Avg height: 10 (optimal: 10)
//
// === Skewed BST (sequential insertion) ===
// Search time: 0.0856 seconds
// Height: 1000 (worst case: 1000)
//
// Balanced is 71.33x faster

Edge Cases and Error Handling

Robust BST implementations must handle edge cases:

RobustBST.php

<?php

declare(strict_types=1);

require_once 'TreeNode.php';

class RobustBST
{
    private ?TreeNode $root = null;
    private int $maxSize = 10000;
    private int $size = 0;

    public function insert(mixed $value): void
    {
        // Edge case: Prevent overflow
        if ($this->size >= $this->maxSize) {
            throw new OverflowException(
                "Tree size limit reached ({$this->maxSize} nodes)"
            );
        }

        // Edge case: Validate input
        if ($value === null) {
            throw new InvalidArgumentException("Cannot insert null value");
        }

        if (!is_numeric($value) && !is_string($value)) {
            throw new InvalidArgumentException(
                "Value must be numeric or string"
            );
        }

        $this->root = $this->insertNode($this->root, $value);
        $this->size++;
    }

    private function insertNode(?TreeNode $node, mixed $value): TreeNode
    {
        if ($node === null) {
            return new TreeNode($value);
        }

        // Handle duplicates (optional: keep, skip, or count)
        if ($value === $node->data) {
            // Option 1: Skip duplicates
            $this->size--; // Compensate for size++ in insert()
            return $node;

            // Option 2: Keep count
            // $node->count = ($node->count ?? 1) + 1;
            // return $node;
        }

        if ($value < $node->data) {
            $node->left = $this->insertNode($node->left, $value);
        } else {
            $node->right = $this->insertNode($node->right, $value);
        }

        return $node;
    }

    public function search(mixed $value): ?TreeNode
    {
        // Edge case: Empty tree
        if ($this->root === null) {
            return null;
        }

        // Edge case: Invalid value
        if ($value === null) {
            throw new InvalidArgumentException("Cannot search for null");
        }

        return $this->searchNode($this->root, $value);
    }

    private function searchNode(?TreeNode $node, mixed $value): ?TreeNode
    {
        if ($node === null || $node->data === $value) {
            return $node;
        }

        if ($value < $node->data) {
            return $this->searchNode($node->left, $value);
        } else {
            return $this->searchNode($node->right, $value);
        }
    }

    public function delete(mixed $value): bool
    {
        // Edge case: Empty tree
        if ($this->root === null) {
            return false;
        }

        // Edge case: Invalid value
        if ($value === null) {
            throw new InvalidArgumentException("Cannot delete null");
        }

        $sizeBefore = $this->size;
        $this->root = $this->deleteNode($this->root, $value);

        // Check if deletion occurred
        if ($sizeBefore === $this->size) {
            return false; // Value not found
        }

        return true;
    }

    private function deleteNode(?TreeNode $node, mixed $value): ?TreeNode
    {
        if ($node === null) {
            return null;
        }

        if ($value < $node->data) {
            $node->left = $this->deleteNode($node->left, $value);
        } elseif ($value > $node->data) {
            $node->right = $this->deleteNode($node->right, $value);
        } else {
            $this->size--;

            // Case 1: Leaf node
            if ($node->left === null && $node->right === null) {
                return null;
            }

            // Case 2: One child
            if ($node->left === null) {
                return $node->right;
            }
            if ($node->right === null) {
                return $node->left;
            }

            // Case 3: Two children
            $successor = $this->findMin($node->right);
            $node->data = $successor->data;
            $node->right = $this->deleteNode($node->right, $successor->data);
            $this->size++; // Compensate for decrement above
        }

        return $node;
    }

    public function findMin(?TreeNode $node = null): ?TreeNode
    {
        if ($node === null) {
            $node = $this->root;
        }

        // Edge case: Empty tree
        if ($node === null) {
            throw new UnderflowException("Tree is empty");
        }

        while ($node->left !== null) {
            $node = $node->left;
        }

        return $node;
    }

    public function clear(): void
    {
        // Help garbage collection
        $this->clearNode($this->root);
        $this->root = null;
        $this->size = 0;
    }

    private function clearNode(?TreeNode $node): void
    {
        if ($node === null) {
            return;
        }

        $this->clearNode($node->left);
        $this->clearNode($node->right);

        // Break references
        $node->left = null;
        $node->right = null;
    }
}

Framework Integration

Laravel: BST-based Cache Service

app/Services/TreeCacheService.php

<?php

declare(strict_types=1);

namespace App\Services;

use Illuminate\Support\Facades\Log;

class TreeCacheService
{
    private RobustBST $cache;

    public function __construct()
    {
        $this->cache = new RobustBST();
    }

    public function set(string $key, mixed $value): void
    {
        // Create cache entry
        $entry = new CacheEntry($key, $value, time());

        try {
            $this->cache->insert($entry);
            Log::info("Cache set", ['key' => $key]);
        } catch (\Exception $e) {
            Log::error("Cache set failed", [
                'key' => $key,
                'error' => $e->getMessage()
            ]);
        }
    }

    public function get(string $key): mixed
    {
        $entry = new CacheEntry($key, null, 0);
        $found = $this->cache->search($entry);

        if ($found === null) {
            Log::debug("Cache miss", ['key' => $key]);
            return null;
        }

        Log::debug("Cache hit", ['key' => $key]);
        return $found->data->value;
    }

    public function has(string $key): bool
    {
        $entry = new CacheEntry($key, null, 0);
        return $this->cache->search($entry) !== null;
    }

    public function delete(string $key): bool
    {
        $entry = new CacheEntry($key, null, 0);
        return $this->cache->delete($entry);
    }
}

class CacheEntry
{
    public function __construct(
        public string $key,
        public mixed $value,
        public int $timestamp
    ) {}

    // Implement comparison for BST
    public function __toString(): string
    {
        return $this->key;
    }
}

Symfony: BST-based Index Service

src/Service/IndexService.php

<?php

declare(strict_types=1);

namespace App\Service;

use App\Entity\Document;
use Doctrine\ORM\EntityManagerInterface;

class IndexService
{
    private RobustBST $index;

    public function __construct(
        private EntityManagerInterface $em
    ) {
        $this->index = new RobustBST();
        $this->buildIndex();
    }

    private function buildIndex(): void
    {
        $documents = $this->em
            ->getRepository(Document::class)
            ->findAll();

        foreach ($documents as $doc) {
            $this->index->insert($doc->getId());
        }
    }

    public function search(int $docId): ?Document
    {
        $node = $this->index->search($docId);

        if ($node === null) {
            return null;
        }

        return $this->em
            ->getRepository(Document::class)
            ->find($docId);
    }

    public function addDocument(Document $doc): void
    {
        $this->em->persist($doc);
        $this->em->flush();

        $this->index->insert($doc->getId());
    }

    public function removeDocument(int $docId): void
    {
        $doc = $this->search($docId);

        if ($doc !== null) {
            $this->em->remove($doc);
            $this->em->flush();

            $this->index->delete($docId);
        }
    }

    public function rebuildIndex(): void
    {
        $this->index->clear();
        $this->buildIndex();
    }
}

Security Considerations

1. Prevent Stack Overflow from Deep Recursion

SecureBST.php

<?php

declare(strict_types=1);

require_once 'RobustBST.php';

class SecureBST extends RobustBST
{
    private int $maxDepth = 100;

    private function insertNode(?TreeNode $node, mixed $value, int $depth = 0): TreeNode
    {
        // Prevent stack overflow
        if ($depth > $this->maxDepth) {
            throw new RuntimeException(
                "Maximum tree depth exceeded. Tree may be unbalanced."
            );
        }

        if ($node === null) {
            return new TreeNode($value);
        }

        if ($value < $node->data) {
            $node->left = $this->insertNode($node->left, $value, $depth + 1);
        } elseif ($value > $node->data) {
            $node->right = $this->insertNode($node->right, $value, $depth + 1);
        }

        return $node;
    }
}

2. Validate and Sanitize Input

SecureBSTInputValidation.php

<?php

declare(strict_types=1);

require_once 'RobustBST.php';

class SecureBST extends RobustBST
{
    public function insert(mixed $value): void
    {
        // Sanitize string input
        if (is_string($value)) {
            $value = htmlspecialchars($value, ENT_QUOTES, 'UTF-8');

            // Prevent excessively long strings
            if (strlen($value) > 255) {
                throw new InvalidArgumentException("Value too long (max 255 chars)");
            }
        }

        // Prevent object injection
        if (is_object($value)) {
            throw new InvalidArgumentException("Cannot insert objects");
        }

        // Prevent array injection
        if (is_array($value)) {
            throw new InvalidArgumentException("Cannot insert arrays");
        }

        parent::insert($value);
    }
}

3. Rate Limiting for Operations

ThrottledBST.php

<?php

declare(strict_types=1);

require_once 'RobustBST.php';

class ThrottledBST extends RobustBST
{
    private int $operationCount = 0;
    private float $lastReset;
    private int $maxOperationsPerSecond = 10000;

    public function __construct()
    {
        parent::__construct();
        $this->lastReset = microtime(true);
    }

    private function checkThrottle(): void
    {
        $now = microtime(true);

        if ($now - $this->lastReset >= 1.0) {
            $this->operationCount = 0;
            $this->lastReset = $now;
        }

        if ($this->operationCount >= $this->maxOperationsPerSecond) {
            throw new RuntimeException("Rate limit exceeded");
        }

        $this->operationCount++;
    }

    public function insert(mixed $value): void
    {
        $this->checkThrottle();
        parent::insert($value);
    }

    public function search(mixed $value): ?TreeNode
    {
        $this->checkThrottle();
        return parent::search($value);
    }
}

Common Pitfalls and Solutions

Pitfall 1: Not Handling Duplicates

// BAD: Duplicates create unexpected behavior
class BadBST
{
    private function insertNode(?TreeNode $node, mixed $value): TreeNode
    {
        if ($node === null) {
            return new TreeNode($value);
        }

        if ($value < $node->data) {
            $node->left = $this->insertNode($node->left, $value);
        } else {
            // What if value === node->data?
            $node->right = $this->insertNode($node->right, $value);
        }

        return $node;
    }
}

// GOOD: Explicit duplicate handling
class GoodBST
{
    private function insertNode(?TreeNode $node, mixed $value): TreeNode
    {
        if ($node === null) {
            return new TreeNode($value);
        }

        if ($value === $node->data) {
            // Option 1: Skip duplicates
            return $node;

            // Option 2: Keep count
            // $node->count = ($node->count ?? 1) + 1;
            // return $node;

            // Option 3: Allow duplicates (use <=)
            // $node->left = $this->insertNode($node->left, $value);
            // return $node;
        }

        if ($value < $node->data) {
            $node->left = $this->insertNode($node->left, $value);
        } else {
            $node->right = $this->insertNode($node->right, $value);
        }

        return $node;
    }
}

Pitfall 2: Incorrect Deletion of Node with Two Children

// BAD: Loses right subtree of successor
class BadBST
{
    private function deleteNode(?TreeNode $node, mixed $value): ?TreeNode
    {
        // ... find node ...

        // Two children case
        if ($node->left !== null && $node->right !== null) {
            $successor = $this->findMin($node->right);
            $node->data = $successor->data;
            // FORGOT: Delete successor from right subtree
            return $node;
        }

        return $node;
    }
}

// GOOD: Properly delete successor
class GoodBST
{
    private function deleteNode(?TreeNode $node, mixed $value): ?TreeNode
    {
        // ... find node ...

        // Two children case
        if ($node->left !== null && $node->right !== null) {
            $successor = $this->findMin($node->right);
            $node->data = $successor->data;
            // Recursively delete successor
            $node->right = $this->deleteNode($node->right, $successor->data);
            return $node;
        }

        return $node;
    }
}

Pitfall 3: Not Returning Updated Node in Recursive Functions

// BAD: Changes not propagated
class BadBST
{
    private function insertNode(?TreeNode $node, mixed $value): TreeNode
    {
        if ($node === null) {
            return new TreeNode($value);
        }

        if ($value < $node->data) {
            // FORGOT: Assign return value
            $this->insertNode($node->left, $value);
        } else {
            $this->insertNode($node->right, $value);
        }

        return $node;
    }
}

// GOOD: Always assign and return
class GoodBST
{
    private function insertNode(?TreeNode $node, mixed $value): TreeNode
    {
        if ($node === null) {
            return new TreeNode($value);
        }

        if ($value < $node->data) {
            $node->left = $this->insertNode($node->left, $value); // Assign!
        } else {
            $node->right = $this->insertNode($node->right, $value); // Assign!
        }

        return $node;
    }
}

Pitfall 4: Creating Skewed Trees with Sequential Input

// BAD: Sequential insertion creates linked list
$bst = new BinarySearchTree();
for ($i = 1; $i <= 1000; $i++) {
    $bst->insert($i); // Creates skewed tree: O(n) operations!
}

// GOOD: Shuffle or use balanced insertion
$values = range(1, 1000);
shuffle($values); // Randomize to get better balance

$bst = new BinarySearchTree();
foreach ($values as $value) {
    $bst->insert($value); // More balanced tree
}

// BETTER: Build balanced tree from sorted array
$sorted = range(1, 1000);
$balancedRoot = sortedArrayToBST($sorted); // O(log n) guaranteed

Pitfall 5: Memory Leaks with Circular References

// BAD: Parent pointers can create cycles
class BadTreeNode
{
    public ?BadTreeNode $left = null;
    public ?BadTreeNode $right = null;
    public ?BadTreeNode $parent = null; // Circular reference!

    public function __construct(public mixed $data) {}
}

// GOOD: Properly cleanup or avoid parent pointers
class GoodBST
{
    public function clear(): void
    {
        $this->clearNode($this->root);
        $this->root = null;
    }

    private function clearNode(?TreeNode $node): void
    {
        if ($node === null) {
            return;
        }

        // Post-order cleanup
        $this->clearNode($node->left);
        $this->clearNode($node->right);

        // Break all references
        $node->left = null;
        $node->right = null;
        $node->parent = null; // If using parent pointers
    }

    public function __destruct()
    {
        $this->clear();
    }
}

Practice Exercises

Exercise 1: Serialize and Deserialize BST

Convert BST to string and back:

exercise-serialize-bst.php

<?php

declare(strict_types=1);

require_once 'TreeNode.php';

function serialize(?TreeNode $root): string
{
    // Your code here
}

function deserialize(string $data): ?TreeNode
{
    // Your code here
}

Exercise 2: BST Iterator

Create an iterator that returns nodes in sorted order:

exercise-bst-iterator.php

<?php

declare(strict_types=1);

require_once 'TreeNode.php';

class BSTIterator
{
    public function __construct(?TreeNode $root) {}

    public function hasNext(): bool {}

    public function next(): int {}
}

Exercise 3: Merge Two BSTs

Merge two BSTs into one balanced BST:

exercise-merge-bsts.php

<?php

declare(strict_types=1);

require_once 'TreeNode.php';

function mergeBSTs(?TreeNode $root1, ?TreeNode $root2): ?TreeNode
{
    // Your code here
}

Key Takeaways

• Trees are hierarchical structures with nodes and edges
• Binary trees have at most 2 children per node
• BSTs maintain sorted order: left < parent < right
• BST operations are O(log n) average, O(n) worst
• Deletion has 3 cases: leaf, one child, two children
• Inorder traversal of BST yields sorted sequence
• Recursive implementations are elegant but risk stack overflow
• Iterative implementations avoid stack overflow and offer better performance
• Balanced trees needed to guarantee O(log n) performance
• Common applications: dictionaries, file systems, databases

What’s Next

In the next chapter, we’ll explore Tree Traversal Algorithms, learning different ways to visit all nodes in a tree systematically.

💻 Code Samples

All code examples from this chapter are available in the GitHub repository:

View Chapter 18 Code Samples

Clone the repository to run examples:

git clone https://github.com/dalehurley/codewithphp.git
cd codewithphp/code/php-algorithms/chapter-18
php 01-*.php

---

Continue to Chapter 19: Tree Traversal Algorithms.