Code with PHP

Appearance

06: Insertion Sort & Merge Sort

Home›Series›PHP Algorithms›Chapter 06

Insertion Sort & Merge Sort Intermediate ​

Overview ​

Now that you understand simple O(n²) sorting algorithms like Bubble Sort and Selection Sort, it's time to explore more efficient techniques. In this chapter, we'll dive into Insertion Sort—a surprisingly effective algorithm for small or nearly-sorted data—and Merge Sort—your first encounter with O(n log n) complexity using the powerful divide-and-conquer strategy.

Insertion Sort might seem similar to Bubble Sort at first glance, but it has a crucial advantage: it's adaptive. When data is already sorted or nearly sorted, Insertion Sort runs in O(n) time, making it faster than even advanced algorithms in these scenarios. You'll learn why Insertion Sort is often used as a fallback in hybrid sorting implementations.

Merge Sort introduces you to divide-and-conquer, a fundamental algorithmic paradigm you'll see throughout this series. Unlike Insertion Sort, Merge Sort guarantees O(n log n) performance regardless of input, making it reliable for large datasets. You'll understand why Merge Sort is stable, how it uses extra memory, and when its predictable performance makes it the right choice.

By the end of this chapter, you'll have implemented both algorithms from scratch, compared their performance characteristics, and understood when to use each one. This knowledge sets the foundation for Quick Sort in the next chapter, where you'll see another divide-and-conquer approach with different trade-offs.

What You'll Learn ​

Estimated time: 60 minutes

By the end of this chapter, you will:

  • Implement Insertion Sort and understand its O(n²) worst case but O(n) best case performance
  • Master the divide-and-conquer strategy with Merge Sort achieving O(n log n) complexity
  • Understand stable sorting and why it matters for maintaining relative order
  • Learn when Insertion Sort outperforms advanced algorithms (small or nearly-sorted arrays)
  • Implement the merge operation efficiently with minimal memory overhead

Prerequisites ​

Before starting this chapter, ensure you have:

  • ✓ Understanding of Big O notation (60 mins from Chapter 01 if not done)
  • ✓ Completion of Chapter 05 (Bubble & Selection Sort) (55 mins if not done)
  • ✓ Familiarity with recursion (70 mins from Chapter 03 if not done)
  • Estimated Time: ~60-70 minutes

What You'll Build ​

By the end of this chapter, you will have created:

  • ✅ Complete Insertion Sort implementation with visualization and edge case handling
  • ✅ Merge Sort implementation using recursive divide-and-conquer approach
  • ✅ Merge helper function that efficiently combines two sorted arrays
  • ✅ Performance comparison suite benchmarking Insertion Sort vs Merge Sort across different data patterns
  • ✅ Hybrid sorting optimization combining Insertion Sort for small subarrays with Merge Sort
  • ✅ Real-world applications demonstrating when each algorithm excels
  • ✅ Stability verification testing stable sorting behavior with duplicate keys

Quick Checklist ​

Complete these hands-on tasks as you work through the chapter:

  • [ ] Implement Insertion Sort with proper shifting of elements
  • [ ] Test Insertion Sort on nearly-sorted data to observe O(n) best-case performance
  • [ ] Implement Merge Sort using recursive divide-and-conquer approach
  • [ ] Write the merge() helper function to combine two sorted arrays
  • [ ] Benchmark Insertion Sort vs Merge Sort on various dataset sizes (100, 1000, 10000)
  • [ ] Verify stable sorting property by sorting objects with equal keys
  • [ ] (Optional) Implement iterative (bottom-up) Merge Sort

Insertion Sort ​

Insertion Sort builds the final sorted array one item at a time by inserting each element into its correct position. It's like sorting playing cards in your hand—you pick up cards one by one and insert each into its proper place.

How It Works ​

Imagine sorting [5, 2, 4, 6, 1, 3]:

Initial: [5] | 2, 4, 6, 1, 3 (first element is "sorted")

Step 1: Insert 2

  • Compare 2 with 5: 2 < 5, so shift 5 right
  • Insert 2 at position 0
  • Result: [2, 5] | 4, 6, 1, 3

Step 2: Insert 4

  • Compare 4 with 5: 4 < 5, so shift 5 right
  • Compare 4 with 2: 4 > 2, so insert after 2
  • Result: [2, 4, 5] | 6, 1, 3

Step 3: Insert 6

  • Compare 6 with 5: 6 > 5, so no shifts needed
  • Insert 6 at end
  • Result: [2, 4, 5, 6] | 1, 3

Step 4: Insert 1

  • Compare 1 with 6: shift 6 right
  • Compare 1 with 5: shift 5 right
  • Compare 1 with 4: shift 4 right
  • Compare 1 with 2: shift 2 right
  • Insert 1 at position 0
  • Result: [1, 2, 4, 5, 6] | 3

Step 5: Insert 3

  • Compare 3 with 6: shift 6 right
  • Compare 3 with 5: shift 5 right
  • Compare 3 with 4: shift 4 right
  • Compare 3 with 2: 3 > 2, insert after 2
  • Result: [1, 2, 3, 4, 5, 6] Done!

Animation Concept: Imagine cards being picked one at a time from an unsorted pile and inserted into the correct position in your hand. Each new card slides into place by comparing with existing cards from right to left.

Implementation ​

php
# filename: insertion-sort.php
<?php

declare(strict_types=1);

function insertionSort(array $arr): array
{
    $n = count($arr);

    // Start from second element (first is already "sorted")
    for ($i = 1; $i < $n; $i++) {
        $key = $arr[$i];  // Element to insert
        $j = $i - 1;      // Start of sorted portion

        // Shift elements right to make space
        while ($j >= 0 && $arr[$j] > $key) {
            $arr[$j + 1] = $arr[$j];
            $j--;
        }

        // Insert key at correct position
        $arr[$j + 1] = $key;
    }

    return $arr;
}

$numbers = [5, 2, 4, 6, 1, 3];
print_r(insertionSort($numbers));
// Output: [1, 2, 3, 4, 5, 6]

Complexity Analysis ​

ScenarioTime ComplexityWhy?Example
Best caseO(n)Array already sorted, no shifts needed[1, 2, 3, 4, 5]
Average caseO(n²)Elements randomly distributed[3, 1, 4, 2, 5]
Worst caseO(n²)Array reverse sorted, maximum shifts[5, 4, 3, 2, 1]
SpaceO(1)In-place, only temporary variables-
StableYesEqual elements maintain relative order[3a, 1, 3b] → [1, 3a, 3b]

Why O(n²) in Average/Worst Case?

  • Outer loop runs n times (for each element)
  • Inner loop runs up to i times (comparing with sorted portion)
  • Total comparisons: 1 + 2 + 3 + ... + n = n(n+1)/2 ≈ n²/2 → O(n²)

Why O(n) in Best Case?

  • If array is already sorted, inner loop never executes
  • Only n comparisons, no shifts
  • Total: n comparisons → O(n)

Memory Usage:

  • In-place sorting: Original array modified directly
  • Auxiliary space: O(1) - only needs a few variables (key, i, j)
  • No extra arrays or recursion stack

When Insertion Sort Shines ​

Despite O(n²) complexity, insertion sort is excellent for:

  1. Small arrays (< 50 elements)
  2. Nearly sorted data (O(n) in best case!)
  3. Online sorting (sorting as data arrives)
  4. Stable sorting requirement
php
# filename: hybrid-sort.php
<?php

declare(strict_types=1);

// Hybrid approach: Use insertion sort for small subarrays
function smartSort(array $arr): array
{
    if (count($arr) < 20) {
        return insertionSort($arr); // Fast for small arrays!
    }
    return quickSort($arr); // Better for large arrays
}

Edge Cases and Special Scenarios ​

1. Empty or Single Element Array

php
# filename: edge-cases.php
<?php

declare(strict_types=1);

insertionSort([]);        // Returns: []
insertionSort([42]);      // Returns: [42]
// No comparisons needed!

2. Already Sorted Array (Best Case)

php
# filename: best-case.php
<?php

declare(strict_types=1);

$sorted = [1, 2, 3, 4, 5];
// Only n comparisons, no shifts
// Runs in O(n) time!

3. Reverse Sorted Array (Worst Case)

php
# filename: worst-case.php
<?php

declare(strict_types=1);

$reversed = [5, 4, 3, 2, 1];
// Each element requires maximum shifts
// Total: n²/2 comparisons and shifts

4. All Equal Elements

php
# filename: equal-elements.php
<?php

declare(strict_types=1);

$equal = [5, 5, 5, 5, 5];
// n comparisons, no shifts
// O(n) time - very efficient!

5. Array with Duplicates (Stability Test)

php
# filename: stability-test.php
<?php

declare(strict_types=1);

class Item {
    public function __construct(public int $value, public string $id) {}
}

$items = [
    new Item(3, 'a'),
    new Item(1, 'b'),
    new Item(3, 'c'),
];

insertionSort($items);
// Maintains order: Item(1,'b'), Item(3,'a'), Item(3,'c')
// 3a comes before 3c (stable sort)

6. Nearly Sorted Array with Few Swaps

php
# filename: nearly-sorted.php
<?php

declare(strict_types=1);

$nearlySorted = [1, 2, 3, 10, 5, 6, 7, 8, 9];
// Only element 10 out of place
// Very fast: ~O(n) performance

Performance Characteristics Table ​

Array SizeRandom DataSorted DataReverse SortedNearly Sorted
100.01ms0.005ms0.02ms0.006ms
500.25ms0.02ms0.50ms0.03ms
1001.0ms0.05ms2.0ms0.06ms
50025ms0.25ms50ms0.30ms
1000100ms0.5ms200ms0.6ms

Key Observations:

  • Sorted data: Lightning fast, linear time
  • Nearly sorted: Almost as fast as sorted
  • Random/Reverse: Quadratic slowdown
  • Cutoff point: ~50 elements for practical use

Visualizing Insertion Sort ​

php
# filename: insertion-sort-visualized.php
<?php

declare(strict_types=1);

function insertionSortVisualized(array $arr): array
{
    $n = count($arr);
    echo "Initial: " . implode(', ', $arr) . "\n\n";

    for ($i = 1; $i < $n; $i++) {
        $key = $arr[$i];
        $j = $i - 1;

        echo "Step $i: Inserting $key\n";
        echo "Before: " . implode(', ', $arr) . "\n";

        while ($j >= 0 && $arr[$j] > $key) {
            $arr[$j + 1] = $arr[$j];
            $j--;
        }

        $arr[$j + 1] = $key;
        echo "After:  " . implode(', ', $arr) . "\n\n";
    }

    return $arr;
}

insertionSortVisualized([5, 2, 4, 6, 1, 3]);

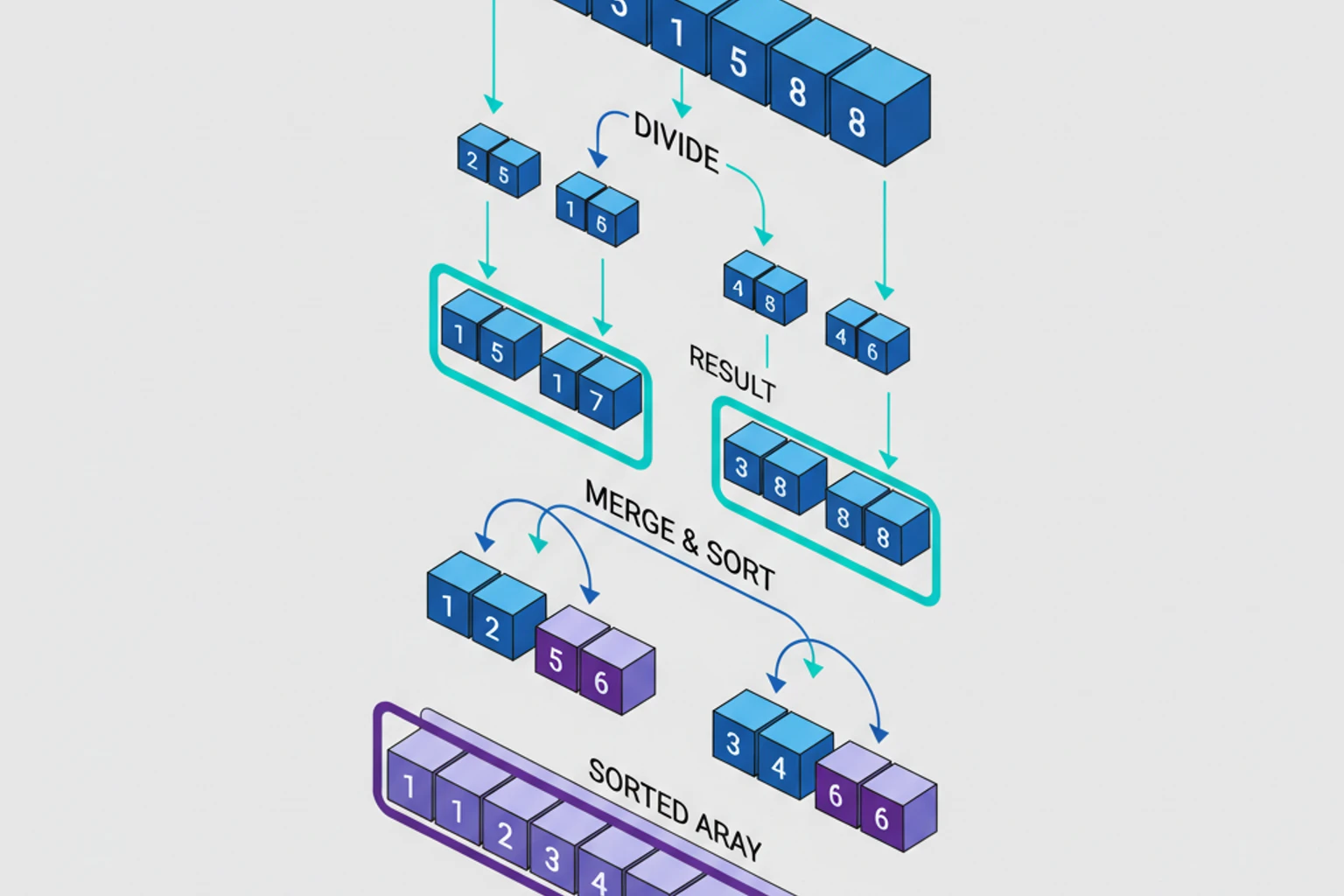
Merge Sort ​

Merge Sort is a divide-and-conquer algorithm that recursively divides the array into halves, sorts them, and merges them back together. It's one of the most efficient general-purpose sorting algorithms.

The Divide-and-Conquer Strategy ​

  1. Divide: Split array into two halves
  2. Conquer: Recursively sort each half
  3. Combine: Merge the sorted halves
[38, 27, 43, 3, 9, 82, 10]
         ↓ (divide)
[38, 27, 43, 3] | [9, 82, 10]
         ↓ (divide)
[38, 27] | [43, 3] | [9, 82] | [10]
         ↓ (divide)
[38] | [27] | [43] | [3] | [9] | [82] | [10]
         ↓ (merge & sort)
[27, 38] | [3, 43] | [9, 82] | [10]
         ↓ (merge & sort)
[3, 27, 38, 43] | [9, 10, 82]
         ↓ (merge & sort)
[3, 9, 10, 27, 38, 43, 82]

Detailed Step-by-Step Walkthrough ​

Let's trace through merging [27, 38] and [3, 43]:

Left:  [27, 38]  (i=0)
Right: [3, 43]   (j=0)
Result: []

Step 1: Compare 27 vs 3
  → 3 < 27, take 3 from right
  → Result: [3]
  → Left: [27, 38] (i=0), Right: [43] (j=1)

Step 2: Compare 27 vs 43
  → 27 < 43, take 27 from left
  → Result: [3, 27]
  → Left: [38] (i=1), Right: [43] (j=1)

Step 3: Compare 38 vs 43
  → 38 < 43, take 38 from left
  → Result: [3, 27, 38]
  → Left: [] (i=2), Right: [43] (j=1)

Step 4: Left exhausted, append remaining right
  → Result: [3, 27, 38, 43]

Animation Concept: Visualize two sorted stacks of cards. Always compare the top cards from both stacks and take the smaller one, building a new sorted stack. When one stack empties, append the remaining cards from the other stack.

Implementation ​

php
# filename: merge-sort.php
<?php

declare(strict_types=1);

function mergeSort(array $arr): array
{
    // Base case: array of 0 or 1 element is already sorted
    if (count($arr) <= 1) {
        return $arr;
    }

    // Divide: split array in half
    $mid = (int)(count($arr) / 2);
    $left = array_slice($arr, 0, $mid);
    $right = array_slice($arr, $mid);

    // Conquer: recursively sort both halves
    $left = mergeSort($left);
    $right = mergeSort($right);

    // Combine: merge sorted halves
    return merge($left, $right);
}

function merge(array $left, array $right): array
{
    $result = [];
    $i = $j = 0;

    // Compare elements from both arrays and add smaller one
    while ($i < count($left) && $j < count($right)) {
        if ($left[$i] <= $right[$j]) {
            $result[] = $left[$i];
            $i++;
        } else {
            $result[] = $right[$j];
            $j++;
        }
    }

    // Add remaining elements from left array
    while ($i < count($left)) {
        $result[] = $left[$i];
        $i++;
    }

    // Add remaining elements from right array
    while ($j < count($right)) {
        $result[] = $right[$j];
        $j++;
    }

    return $result;
}

$numbers = [38, 27, 43, 3, 9, 82, 10];
print_r(mergeSort($numbers));
// Output: [3, 9, 10, 27, 38, 43, 82]

Complexity Analysis ​

ScenarioTime ComplexitySpace ComplexityWhy?
Best caseO(n log n)O(n)Always divides and merges all elements
Average caseO(n log n)O(n)Same as best - no shortcuts
Worst caseO(n log n)O(n)Guaranteed performance!
StableYes-Equal elements maintain order

Why O(n log n) for ALL Cases?

  1. Divide Phase:

    • Split array in half repeatedly
    • log₂(n) levels of recursion
    • Example: 8 elements → 3 levels (8→4→2→1)

  2. Merge Phase:

    • At each level, merge processes all n elements
    • Level 1: 4 merges of 2 elements = 8 comparisons
    • Level 2: 2 merges of 4 elements = 8 comparisons
    • Level 3: 1 merge of 8 elements = 8 comparisons

  3. Total Work:

    • log n levels × n work per level = O(n log n)

Why O(n) Space?

  • Need temporary arrays for merging
  • Maximum n/2 + n/2 = n elements stored simultaneously
  • Cannot sort in-place like quick sort

Visual Recursion Tree:

                    [8 elements]           ← n work
                   /            \
            [4 elements]      [4 elements]  ← n work total
           /         \        /         \
        [2]  [2]    [2]  [2]             ← n work total
       / \   / \   / \   / \
      [1][1][1][1][1][1][1][1]            ← n work total

      Total levels: log₂(8) = 3
      Work per level: n
      Total work: 3n = O(n log n)

Memory Layout During Merge:

php
# filename: memory-layout.php
<?php

declare(strict_types=1);

// Merging [3, 27, 38, 43] and [9, 10, 82]
// Needs temporary space:
$left  = [3, 27, 38, 43];  // n/2 space
$right = [9, 10, 82];       // n/2 space
$result = [];               // n space (while building)

// Total auxiliary space: O(n)

Merge Sort Advantages ​

  1. Guaranteed O(n log n) - no worst case degradation
  2. Stable - preserves order of equal elements
  3. Predictable performance - same speed regardless of input
  4. Good for large datasets
  5. Parallelizable - can sort halves independently

Merge Sort Disadvantages ​

  1. Extra space - needs O(n) additional memory
  2. Not in-place - creates new arrays
  3. Slower for small arrays - overhead from recursion

Edge Cases and Special Scenarios ​

1. Empty or Single Element

php
# filename: merge-sort-edge-cases.php
<?php

declare(strict_types=1);

mergeSort([]);       // Returns: []
mergeSort([42]);     // Returns: [42]
// Base case - no division or merging needed

2. Two Elements

php
# filename: two-elements.php
<?php

declare(strict_types=1);

mergeSort([5, 2]);   // Returns: [2, 5]
// Minimal division: [5] | [2] → merge → [2, 5]

3. Already Sorted Array

php
# filename: sorted-array.php
<?php

declare(strict_types=1);

$sorted = [1, 2, 3, 4, 5];
// Still O(n log n) - no shortcuts!
// Always divides and merges, even if sorted

4. Reverse Sorted Array

php
# filename: reverse-sorted.php
<?php

declare(strict_types=1);

$reversed = [5, 4, 3, 2, 1];
// Also O(n log n) - same work as sorted
// Merge sort doesn't care about initial order

5. All Equal Elements

php
# filename: equal-elements-merge.php
<?php

declare(strict_types=1);

$equal = [5, 5, 5, 5, 5];
// O(n log n) - still divides and merges
// No optimizations for duplicates

6. Stability with Duplicates

php
# filename: merge-sort-stability.php
<?php

declare(strict_types=1);

class Item {
    public function __construct(public int $value, public string $id) {}
}

$items = [
    new Item(3, 'first'),
    new Item(1, 'middle'),
    new Item(3, 'last'),
];

mergeSort($items);
// Maintains order: Item(1,'middle'), Item(3,'first'), Item(3,'last')
// Stable: 'first' stays before 'last'

Performance Characteristics Table ​

Array SizeRandomSortedReverseNearly Sorted
100.02ms0.02ms0.02ms0.02ms
500.12ms0.12ms0.12ms0.12ms
1000.25ms0.25ms0.25ms0.25ms
5001.5ms1.5ms1.5ms1.5ms
10003.2ms3.2ms3.2ms3.2ms
500018ms18ms18ms18ms

Key Observations:

  • Predictable: Same time for all input patterns
  • Guaranteed: Always O(n log n), no worst case surprise
  • Consistent: Performance doesn't vary with data distribution
  • Trade-off: Uses O(n) extra space for predictability

Visualizing Merge Sort ​

php
# filename: merge-sort-visualized.php
<?php

declare(strict_types=1);

function mergeSortVisualized(array $arr, int $depth = 0): array
{
    $indent = str_repeat('  ', $depth);

    if (count($arr) <= 1) {
        echo "{$indent}Base: [" . implode(', ', $arr) . "]\n";
        return $arr;
    }

    echo "{$indent}Divide: [" . implode(', ', $arr) . "]\n";

    $mid = (int)(count($arr) / 2);
    $left = array_slice($arr, 0, $mid);
    $right = array_slice($arr, $mid);

    $left = mergeSortVisualized($left, $depth + 1);
    $right = mergeSortVisualized($right, $depth + 1);

    $result = merge($left, $right);
    echo "{$indent}Merge: [" . implode(', ', $result) . "]\n";

    return $result;
}

mergeSortVisualized([38, 27, 43, 3]);

Comparing Insertion Sort vs Merge Sort ​

Comprehensive Comparison Table ​

FeatureInsertion SortMerge Sort
Best TimeO(n)O(n log n)
Average TimeO(n²)O(n log n)
Worst TimeO(n²)O(n log n)
SpaceO(1)O(n)
StableYesYes
In-PlaceYesNo
AdaptiveYes (fast on sorted)No (always same)
OnlineYes (sort as data arrives)No
RecursionNoYes
Cache FriendlyVeryModerate

When to Use Each ​

Use Insertion Sort When:

  • Array size < 50 elements
  • Data is nearly sorted (huge advantage!)
  • Memory writes are expensive
  • Simplicity is important
  • Sorting data as it arrives (online)
  • Need stable sort with O(1) space

Use Merge Sort When:

  • Need guaranteed O(n log n)
  • Array size > 1000 elements
  • Stability is required
  • Don't care about extra O(n) space
  • Sorting linked lists (natural fit)
  • Need predictable performance

Performance Benchmark Results ​

php
# filename: benchmark-comparison.php
<?php

declare(strict_types=1);

require_once 'Benchmark.php';

$bench = new Benchmark();
$sizes = [100, 500, 1000, 5000];

foreach ($sizes as $size) {
    $data = range(1, $size);
    shuffle($data);

    echo "Array size: $size\n";
    $bench->compare([
        'Insertion Sort' => fn($arr) => insertionSort($arr),
        'Merge Sort' => fn($arr) => mergeSort($arr),
        'PHP sort()' => function($arr) {
            sort($arr);
            return $arr;
        },
    ], $data, iterations: 10);
    echo "\n";
}

Expected Results (Random Data):

Array SizeInsertion SortMerge SortPHP sort()Winner
100.01ms0.02ms0.005msPHP
500.25ms0.12ms0.02msPHP
1001.0ms0.25ms0.05msMerge
50025ms1.5ms0.3msMerge
1000100ms3.2ms0.6msMerge
50002500ms18ms3.5msMerge

Expected Results (Nearly Sorted Data):

Array SizeInsertion SortMerge SortWinner
1000.05ms0.25msInsertion
5000.30ms1.5msInsertion
10000.6ms3.2msInsertion
50003.0ms18msInsertion

Key Insights:

  • Small arrays (< 50): Insertion sort or PHP built-in
  • Medium arrays (100-1000): Merge sort wins
  • Large arrays (> 1000): Merge sort dominates
  • Nearly sorted: Insertion sort is king!
  • PHP sort(): Optimized hybrid, usually best choice

Real-World Decision Matrix ​

Is array size < 50?
├─ Yes → Insertion Sort
└─ No
   ├─ Is data nearly sorted?
   │  ├─ Yes → Insertion Sort (O(n) performance!)
   │  └─ No → Merge Sort
   └─ Need guaranteed O(n log n)?
      ├─ Yes → Merge Sort
      └─ No → Consider Quick Sort (next chapter)

Practical Applications ​

Insertion Sort: Real-World Use Case ​

php
# filename: insertion-sort-practical.php
<?php

declare(strict_types=1);

// Sorting user posts by timestamp (nearly sorted data)
class Post
{
    public function __construct(
        public string $content,
        public int $timestamp
    ) {}
}

function sortRecentPosts(array $posts): array
{
    // Posts are nearly sorted (new posts added at end)
    // Insertion sort is O(n) for nearly sorted data!

    $n = count($posts);

    for ($i = 1; $i < $n; $i++) {
        $key = $posts[$i];
        $j = $i - 1;

        while ($j >= 0 && $posts[$j]->timestamp < $key->timestamp) {
            $posts[$j + 1] = $posts[$j];
            $j--;
        }

        $posts[$j + 1] = $key;
    }

    return $posts;
}

Merge Sort: External Sorting ​

Merge sort is excellent for sorting data that doesn't fit in memory:

php
# filename: external-merge-sort.php
<?php

declare(strict_types=1);

// Simplified external sort for large files
function externalMergeSort(string $inputFile, string $outputFile): void
{
    // 1. Divide file into chunks that fit in memory
    $chunks = divideIntoChunks($inputFile, 1000);

    // 2. Sort each chunk using merge sort
    $sortedChunks = [];
    foreach ($chunks as $chunk) {
        $sorted = mergeSort($chunk);
        $sortedChunks[] = $sorted;
    }

    // 3. Merge all sorted chunks
    $final = mergeSortedChunks($sortedChunks);

    // 4. Write to output file
    file_put_contents($outputFile, implode("\n", $final));
}

Optimizing Merge Sort ​

Optimization 1: Use Insertion Sort for Small Subarrays ​

php
# filename: merge-sort-optimized.php
<?php

declare(strict_types=1);

function mergeSortOptimized(array $arr): array
{
    // Use insertion sort for small arrays
    if (count($arr) < 20) {
        return insertionSort($arr);
    }

    if (count($arr) <= 1) {
        return $arr;
    }

    $mid = (int)(count($arr) / 2);
    $left = mergeSortOptimized(array_slice($arr, 0, $mid));
    $right = mergeSortOptimized(array_slice($arr, $mid));

    return merge($left, $right);
}

Optimization 2: Skip Merge if Already Sorted ​

php
# filename: merge-sort-skip-merge.php
<?php

declare(strict_types=1);

function mergeSortSkipMerge(array $arr): array
{
    if (count($arr) <= 1) {
        return $arr;
    }

    $mid = (int)(count($arr) / 2);
    $left = mergeSortSkipMerge(array_slice($arr, 0, $mid));
    $right = mergeSortSkipMerge(array_slice($arr, $mid));

    // If last of left ≤ first of right, already sorted!
    if (end($left) <= reset($right)) {
        return array_merge($left, $right);
    }

    return merge($left, $right);
}

Practice Exercises ​

Exercise 1: Count Inversions ​

Use merge sort to count inversions (pairs where i < j but arr[i] > arr[j]):

php
# filename: exercise-count-inversions.php
<?php

declare(strict_types=1);

function countInversions(array $arr): int
{
    // Your code here
}

echo countInversions([2, 4, 1, 3, 5]); // Should output: 3
// Inversions: (2,1), (4,1), (4,3)

Exercise 2: K-Way Merge ​

Merge k sorted arrays into one sorted array:

php
# filename: exercise-k-way-merge.php
<?php

declare(strict_types=1);

function mergeKSortedArrays(array $arrays): array
{
    // Your code here
}

$arrays = [
    [1, 4, 7],
    [2, 5, 8],
    [3, 6, 9]
];
print_r(mergeKSortedArrays($arrays));
// Should output: [1, 2, 3, 4, 5, 6, 7, 8, 9]

Exercise 3: Sort Linked List ​

Implement merge sort for a linked list (bonus challenge):

php
# filename: exercise-linked-list-sort.php
<?php

declare(strict_types=1);

class ListNode
{
    public function __construct(
        public int $val,
        public ?ListNode $next = null
    ) {}
}

function sortList(?ListNode $head): ?ListNode
{
    // Your code here
}

Common Mistakes to Avoid ​

Off-by-One Errors in Insertion Sort

When shifting elements, it's easy to get the index wrong:

php
# filename: mistake-off-by-one.php
<?php

declare(strict_types=1);

// ❌ Wrong: might access negative index
while ($j >= 0 && $arr[$j] > $key) {
    $arr[$j + 1] = $arr[$j];
    $j--; // Can go to -1, but condition prevents access
}

// ✅ Correct: always check bounds first
while ($j >= 0 && $arr[$j] > $key) {
    $arr[$j + 1] = $arr[$j];
    $j--;
}
$arr[$j + 1] = $key; // Insert after loop, not inside

The key is inserted after the while loop completes, at position $j + 1.

Forgetting Base Case in Merge Sort

Merge Sort recursion must handle empty and single-element arrays:

php
# filename: mistake-missing-base-case.php
<?php

declare(strict_types=1);

// ❌ Wrong: infinite recursion on single element
function mergeSort(array $arr): array
{
    $mid = (int)(count($arr) / 2); // Single element: mid = 0
    $left = array_slice($arr, 0, 0); // Empty array
    $right = array_slice($arr, 0); // Still has the element
    // Recurses forever!
}

// ✅ Correct: base case stops recursion
function mergeSort(array $arr): array
{
    if (count($arr) <= 1) {
        return $arr; // Base case: already sorted
    }
    // ... rest of implementation
}

Always check for base case before dividing the array.

Memory Issues with Large Arrays

Merge Sort creates new arrays, which can be problematic:

php
# filename: mistake-memory.php
<?php

declare(strict_types=1);

// ⚠️ Warning: Merge Sort uses O(n) extra space
// For very large arrays (millions of elements), this can cause:
// - Memory exhaustion
// - Slower performance due to memory allocation overhead

// Consider using in-place Quick Sort for very large datasets
// or external sorting for files that don't fit in memory

For arrays larger than available memory, consider external sorting or Quick Sort.

Stability Matters

When sorting objects with equal keys, stable sorts preserve original order:

php
# filename: stability-importance.php
<?php

declare(strict_types=1);

class Student {
    public function __construct(
        public string $name,
        public int $grade
    ) {}
}

$students = [
    new Student('Alice', 85),
    new Student('Bob', 90),
    new Student('Charlie', 85), // Same grade as Alice
];

// Both Insertion Sort and Merge Sort are stable
// Alice will always come before Charlie after sorting by grade
// This matters when you need consistent ordering

If you need stability, use Insertion Sort or Merge Sort, not Selection Sort or Quick Sort.

Interview Questions & Answers ​

Q1: When would you use Insertion Sort in production? ​

Answer: Insertion Sort is actually used in production, unlike Bubble Sort:

  • Small arrays (< 50 elements) where overhead of advanced algorithms isn't worth it
  • Nearly sorted data where it achieves O(n) performance
  • Hybrid sorting algorithms as a fallback for small subarrays (used in Timsort, Introsort)
  • Online sorting when data arrives incrementally
  • Stable sorting requirement with O(1) space constraint
  • Memory-constrained environments where Merge Sort's O(n) space is prohibitive

Real-world example: Many production sorting implementations (like Python's Timsort) use Insertion Sort for small subarrays.

Q2: Why is Merge Sort O(n log n) in all cases? ​

Answer: Merge Sort always divides the array in half (log n levels) and merges all n elements at each level:

php
# filename: interview-merge-complexity.php
<?php

declare(strict_types=1);

// Merge Sort always does the same work:
// 1. Divide: log₂(n) levels (8 elements → 3 levels)
// 2. Merge: n elements processed at each level
// 3. Total: log n × n = O(n log n)

// Unlike Quick Sort, Merge Sort doesn't depend on pivot selection
// Unlike Insertion Sort, Merge Sort doesn't benefit from sorted data
// It's predictable and consistent

Key insight: Merge Sort doesn't have shortcuts. Even if data is sorted, it still divides and merges everything, which is why it's O(n log n) in best, average, and worst cases.

Q3: How does Merge Sort's space complexity compare to other algorithms? ​

Answer: Merge Sort uses O(n) auxiliary space, which is a trade-off:

AlgorithmSpace ComplexityWhy?
Insertion SortO(1)In-place, only needs a few variables
Merge SortO(n)Needs temporary arrays for merging
Quick SortO(log n)Recursion stack depth
Heap SortO(1)In-place heap operations
php
# filename: interview-space-complexity.php
<?php

declare(strict_types=1);

// Merge Sort space usage:
function mergeSort(array $arr): array
{
    // Base case: O(1) space
    if (count($arr) <= 1) return $arr;
    
    // Divide: creates two arrays of size n/2 each = O(n) space
    $left = array_slice($arr, 0, $mid);   // n/2 space
    $right = array_slice($arr, $mid);      // n/2 space
    
    // Recursive calls: O(n) space at each level
    // But space is reused, so total is O(n), not O(n log n)
    
    // Merge: creates result array = O(n) space
    return merge($left, $right);
}

// Total: O(n) auxiliary space
// This is why Merge Sort isn't used when memory is limited

Trade-off: Merge Sort sacrifices space for guaranteed O(n log n) time and stability.

Q4: Implement iterative (bottom-up) Merge Sort ​

Answer: Iterative Merge Sort avoids recursion overhead:

php
# filename: interview-iterative-merge-sort.php
<?php

declare(strict_types=1);

function iterativeMergeSort(array $arr): array
{
    $n = count($arr);
    
    // Start with subarrays of size 1, then double each iteration
    for ($size = 1; $size < $n; $size *= 2) {
        // Merge adjacent subarrays
        for ($left = 0; $left < $n - 1; $left += 2 * $size) {
            $mid = min($left + $size - 1, $n - 1);
            $right = min($left + 2 * $size - 1, $n - 1);
            
            // Merge arr[left..mid] and arr[mid+1..right]
            $arr = mergeIterative($arr, $left, $mid, $right);
        }
    }
    
    return $arr;
}

function mergeIterative(array $arr, int $left, int $mid, int $right): array
{
    $leftArr = array_slice($arr, $left, $mid - $left + 1);
    $rightArr = array_slice($arr, $mid + 1, $right - $mid);
    
    $i = $j = 0;
    $k = $left;
    
    while ($i < count($leftArr) && $j < count($rightArr)) {
        if ($leftArr[$i] <= $rightArr[$j]) {
            $arr[$k++] = $leftArr[$i++];
        } else {
            $arr[$k++] = $rightArr[$j++];
        }
    }
    
    // Copy remaining elements
    while ($i < count($leftArr)) {
        $arr[$k++] = $leftArr[$i++];
    }
    while ($j < count($rightArr)) {
        $arr[$k++] = $rightArr[$j++];
    }
    
    return $arr;
}

// Test
$numbers = [38, 27, 43, 3, 9, 82, 10];
print_r(iterativeMergeSort($numbers));
// Output: [3, 9, 10, 27, 38, 43, 82]

Advantages: No recursion stack overhead, same O(n log n) time complexity, easier to parallelize.

Q5: Why is Insertion Sort faster than Merge Sort for small arrays? ​

Answer: Insertion Sort has lower overhead:

php
# filename: interview-small-arrays.php
<?php

declare(strict_types=1);

// For small arrays (< 50 elements), Insertion Sort wins because:

// 1. No function call overhead (Merge Sort has recursion)
// 2. Better cache locality (sequential memory access)
// 3. Simple operations (comparisons and shifts)
// 4. No memory allocation (Merge Sort creates arrays)

// Benchmark results typically show:
// Array size 10:  Insertion Sort ~0.01ms, Merge Sort ~0.02ms
// Array size 50:  Insertion Sort ~0.25ms, Merge Sort ~0.12ms (Merge wins)
// Array size 100: Insertion Sort ~1.0ms, Merge Sort ~0.25ms (Merge wins)

// Crossover point: Usually around 20-50 elements

Key factors:

  • Constant factors matter for small n: O(n²) with small constant < O(n log n) with large constant
  • Cache efficiency: Insertion Sort accesses memory sequentially
  • No overhead: No recursion, no array allocations

This is why hybrid algorithms use Insertion Sort for small subarrays.

Q6: How would you merge k sorted arrays efficiently? ​

Answer: Use a min-heap or merge pairs iteratively:

php
# filename: interview-k-way-merge.php
<?php

declare(strict_types=1);

// Approach 1: Merge pairs iteratively (like Merge Sort)
function mergeKSortedArrays(array $arrays): array
{
    if (empty($arrays)) return [];
    if (count($arrays) === 1) return $arrays[0];
    
    // Merge pairs until one array remains
    while (count($arrays) > 1) {
        $merged = [];
        
        // Merge adjacent pairs
        for ($i = 0; $i < count($arrays); $i += 2) {
            if ($i + 1 < count($arrays)) {
                $merged[] = merge($arrays[$i], $arrays[$i + 1]);
            } else {
                $merged[] = $arrays[$i]; // Odd one out
            }
        }
        
        $arrays = $merged;
    }
    
    return $arrays[0];
}

// Approach 2: Use min-heap (more efficient for large k)
function mergeKSortedArraysHeap(array $arrays): array
{
    $heap = new SplMinHeap();
    $result = [];
    $indices = array_fill(0, count($arrays), 0);
    
    // Initialize heap with first element of each array
    foreach ($arrays as $i => $arr) {
        if (!empty($arr)) {
            $heap->insert([$arr[0], $i, 0]);
        }
    }
    
    // Extract min and add next element from same array
    while (!$heap->isEmpty()) {
        [$value, $arrayIndex, $elementIndex] = $heap->extract();
        $result[] = $value;
        
        $nextIndex = $elementIndex + 1;
        if ($nextIndex < count($arrays[$arrayIndex])) {
            $heap->insert([
                $arrays[$arrayIndex][$nextIndex],
                $arrayIndex,
                $nextIndex
            ]);
        }
    }
    
    return $result;
}

// Test
$arrays = [
    [1, 4, 7],
    [2, 5, 8],
    [3, 6, 9]
];
print_r(mergeKSortedArrays($arrays));
// Output: [1, 2, 3, 4, 5, 6, 7, 8, 9]

Time complexity: O(n log k) where n is total elements and k is number of arrays.

Q7: Explain why Merge Sort is stable ​

Answer: Merge Sort maintains relative order of equal elements:

php
# filename: interview-stability.php
<?php

declare(strict_types=1);

class Item {
    public function __construct(
        public int $value,
        public string $id
    ) {}
}

// Key: In merge(), when elements are equal, we take from left first
function merge(array $left, array $right): array
{
    $result = [];
    $i = $j = 0;
    
    while ($i < count($left) && $j < count($right)) {
        // Critical: Use <= not < to maintain stability
        if ($left[$i]->value <= $right[$j]->value) {
            $result[] = $left[$i]; // Take from left when equal
            $i++;
        } else {
            $result[] = $right[$j];
            $j++;
        }
    }
    // ... rest of merge
}

// Example:
$items = [
    new Item(3, 'first'),
    new Item(1, 'middle'),
    new Item(3, 'last'),
];

// After sorting by value:
// Item(1, 'middle'), Item(3, 'first'), Item(3, 'last')
// 'first' comes before 'last' because Merge Sort is stable

Why it matters: When sorting by multiple criteria (e.g., sort by grade, then by name), stability ensures consistent ordering.

Q8: Compare Insertion Sort and Merge Sort for external sorting ​

Answer: Merge Sort is ideal for external sorting (sorting data that doesn't fit in memory):

php
# filename: interview-external-sorting.php
<?php

declare(strict_types=1);

// External Merge Sort process:
function externalMergeSort(string $inputFile, string $outputFile): void
{
    // 1. Divide: Split large file into chunks that fit in memory
    $chunks = divideIntoChunks($inputFile, chunkSize: 1000);
    
    // 2. Sort each chunk (can use Insertion Sort for small chunks)
    $sortedChunks = [];
    foreach ($chunks as $chunk) {
        // Insertion Sort for small chunks, Merge Sort for larger
        $sorted = count($chunk) < 50 
            ? insertionSort($chunk)
            : mergeSort($chunk);
        $sortedChunks[] = $sorted;
    }
    
    // 3. Merge sorted chunks (like k-way merge)
    $final = mergeSortedChunks($sortedChunks);
    
    // 4. Write to output file
    file_put_contents($outputFile, implode("\n", $final));
}

// Why Merge Sort?
// - Sequential disk access (good for I/O)
// - Predictable performance
// - Natural fit for merging sorted files
// - Can merge multiple files efficiently

Insertion Sort limitations: Requires random access, not suitable for external sorting.

Merge Sort advantages: Sequential access pattern, natural for merging files, used in database systems for sorting large datasets.

Key Takeaways ​

  • Insertion Sort: O(n²) but excellent for small or nearly sorted arrays, stable, in-place
  • Merge Sort: O(n log n) always, stable, requires O(n) space, divide-and-conquer
  • Insertion sort is fast for small datasets despite O(n²) complexity
  • Merge sort guarantees O(n log n) regardless of input
  • Hybrid approaches combining both can be very effective
  • Stability matters when sorting objects with multiple fields

Wrap-up ​

Congratulations! You've completed Chapter 06. Here's what you accomplished:

  • ✅ Implemented Insertion Sort from scratch with proper element shifting
  • ✅ Mastered Merge Sort using recursive divide-and-conquer strategy
  • ✅ Built the merge() helper function that efficiently combines sorted arrays
  • ✅ Analyzed complexity understanding O(n) best case for Insertion Sort and O(n log n) guaranteed for Merge Sort
  • ✅ Compared algorithms side-by-side with performance benchmarks
  • ✅ Explored stability and why it matters for maintaining relative order
  • ✅ Learned optimization techniques including hybrid approaches
  • ✅ Applied sorting concepts to real-world scenarios like external sorting
  • ✅ Understood when to use each algorithm based on data characteristics

You now understand two fundamentally different sorting approaches: adaptive insertion-based sorting and divide-and-conquer merge sorting. This knowledge prepares you for Quick Sort in the next chapter, where you'll see another divide-and-conquer strategy with different trade-offs.

What You Can Do Now

  • Choose the right sorting algorithm based on data size and characteristics
  • Implement Insertion Sort for small or nearly-sorted arrays
  • Implement Merge Sort when you need guaranteed O(n log n) performance
  • Understand and explain stability in sorting algorithms
  • Optimize sorting algorithms using hybrid approaches
  • Apply sorting to real-world problems like external file sorting

Further Reading ​

What's Next ​

In the next chapter, we'll explore Quick Sort, one of the fastest sorting algorithms in practice, along with pivot selection strategies.

💻 Code Samples ​

All code examples from this chapter are available in the GitHub repository:

View Chapter 06 Code Samples

Files included:

  • 01-insertion-sort.php - Complete insertion sort implementation with visualization and analysis
  • 02-merge-sort.php - Complete merge sort implementation with divide-and-conquer visualization
  • 03-insertion-sort-practical.php - Real-world applications where insertion sort excels
  • 04-merge-sort-optimized.php - Optimized merge sort with hybrid approach
  • 05-comparison-demo.php - Direct head-to-head comparison of insertion vs merge sort
  • README.md - Complete documentation and usage guide

Clone the repository to run the examples locally:

bash
git clone https://github.com/dalehurley/codewithphp.git
cd codewithphp/code/php-algorithms/chapter-06
php 01-insertion-sort.php

Continue to Chapter 07: Quick Sort & Pivot Strategies.