20: Balanced Trees: AVL & Red-Black Trees

Balanced Trees: AVL & Red-Black Trees

20: Balanced Trees: AVL & Red-Black Trees Advanced

What You’ll Learn

Understand why BSTs can degrade and how self-balancing solves this
Implement AVL trees with rotation operations (single and double)
Master Red-Black tree properties and insertion rules
Compare AVL vs. Red-Black trees for different use cases
Build self-balancing trees that guarantee O(log n) operations

Prerequisites

Before starting this chapter, you should have:

✓ Complete understanding of binary search trees (Chapter 18)
✓ Mastery of tree traversal algorithms (Chapter 19)
✓ Strong recursion skills (Chapter 3)
✓ Patience for complex rotations and rebalancing logic

Estimated Time: ~70 minutes

Overview

Regular binary search trees can become unbalanced, degrading to O(n) time complexity in the worst case. Imagine inserting sorted data—you’d end up with essentially a linked list! Self-balancing trees maintain logarithmic height automatically through clever rotations and color properties, ensuring O(log n) performance for all operations no matter the insertion order.

In this chapter, you’ll explore two fundamental self-balancing tree structures: AVL trees and Red-Black trees. AVL trees maintain strict balance through height tracking and rotations, while Red-Black trees use color properties to achieve looser but still effective balancing. Both guarantee O(log n) worst-case performance, but they differ in their balancing strategies and use cases.

The Problem with Unbalanced Trees

<?php

declare(strict_types=1);

// Inserting sorted data into a BST creates a linked list
$bst = new BinarySearchTree();
foreach ([1, 2, 3, 4, 5, 6, 7] as $value) {
    $bst->insert($value);
}

// Tree structure becomes:
//     1
//      \
//       2
//        \
//         3
//          \
//           4
//            \
//             5
//              \
//               6
//                \
//                 7

// Height: 7, Search time: O(n) instead of O(log n)

Self-balancing trees solve this by maintaining balance through rotations and color properties. When a tree becomes unbalanced after insertion or deletion, these trees automatically detect the imbalance and perform rotations to restore balance, ensuring the tree height remains logarithmic.

AVL Trees

AVL (Adelson-Velsky and Landis) trees maintain strict balance: the height difference between left and right subtrees (balance factor) of any node is at most 1. This strict balancing ensures the tree height is always bounded by approximately 1.44 * log₂(n), making searches very efficient. However, this strictness means more rotations are needed during insertions and deletions compared to Red-Black trees.

Balance Factor

The balance factor is the key metric that determines if an AVL tree is balanced. It’s calculated as the difference between the heights of the left and right subtrees.

Balance Factor = Height(Left Subtree) - Height(Right Subtree)
Valid values: -1, 0, 1

Why these values? If the balance factor is outside this range, the tree is unbalanced:

Balance factor > 1: Left subtree is too tall (needs right rotation)
Balance factor < -1: Right subtree is too tall (needs left rotation)
Balance factor in [-1, 0, 1]: Tree is balanced, no action needed

AVL Node Implementation

The AVL node extends a standard BST node by tracking the height of the subtree rooted at that node. This height information is crucial for calculating balance factors and determining when rotations are needed.

<?php

declare(strict_types=1);

class AVLNode
{
    public function __construct(
        public mixed $data,
        public ?AVLNode $left = null,
        public ?AVLNode $right = null,
        public int $height = 1  // Height of subtree rooted at this node
    ) {}
}

class AVLTree
{
    private ?AVLNode $root = null;

    // Get height of node
    private function height(?AVLNode $node): int
    {
        return $node?->height ?? 0;
    }

    // Update height of node
    private function updateHeight(AVLNode $node): void
    {
        $node->height = 1 + max(
            $this->height($node->left),
            $this->height($node->right)
        );
    }

    // Get balance factor
    private function getBalance(?AVLNode $node): int
    {
        if ($node === null) {
            return 0;
        }

        return $this->height($node->left) - $this->height($node->right);
    }

    // Right rotation (single rotation)
    // Used when left subtree is taller (Left-Left case)
    //       y                    x
    //      / \                  / \
    //     x   C    =>          A   y
    //    / \                      / \
    //   A   B                    B   C
    //
    // Steps:
    // 1. x becomes the new root
    // 2. y becomes x's right child
    // 3. B (x's right subtree) becomes y's left subtree
    private function rotateRight(AVLNode $y): AVLNode
    {
        $x = $y->left;        // x is the left child of y
        $B = $x->right;       // Save x's right subtree

        // Perform rotation
        $x->right = $y;       // Make y the right child of x
        $y->left = $B;        // Attach B as left child of y

        // Update heights (must update y first, then x)
        $this->updateHeight($y);
        $this->updateHeight($x);

        return $x;            // Return new root
    }

    // Left rotation (single rotation)
    // Used when right subtree is taller (Right-Right case)
    //     x                      y
    //    / \                    / \
    //   A   y      =>          x   C
    //      / \                / \
    //     B   C              A   B
    //
    // Steps:
    // 1. y becomes the new root
    // 2. x becomes y's left child
    // 3. B (y's left subtree) becomes x's right subtree
    private function rotateLeft(AVLNode $x): AVLNode
    {
        $y = $x->right;       // y is the right child of x
        $B = $y->left;        // Save y's left subtree

        // Perform rotation
        $y->left = $x;        // Make x the left child of y
        $x->right = $B;       // Attach B as right child of x

        // Update heights (must update x first, then y)
        $this->updateHeight($x);
        $this->updateHeight($y);

        return $y;            // Return new root
    }

    // Insert a value
    public function insert(mixed $value): void
    {
        $this->root = $this->insertNode($this->root, $value);
    }

    private function insertNode(?AVLNode $node, mixed $value): AVLNode
    {
        // Normal BST insertion
        if ($node === null) {
            return new AVLNode($value);
        }

        if ($value < $node->data) {
            $node->left = $this->insertNode($node->left, $value);
        } elseif ($value > $node->data) {
            $node->right = $this->insertNode($node->right, $value);
        } else {
            // Duplicate values not allowed
            return $node;
        }

        // Update height
        $this->updateHeight($node);

        // Get balance factor to check if tree became unbalanced
        $balance = $this->getBalance($node);

        // Left-Left Case: Left subtree is taller and insertion was in left subtree
        // Solution: Single right rotation
        if ($balance > 1 && $value < $node->left->data) {
            return $this->rotateRight($node);
        }

        // Right-Right Case: Right subtree is taller and insertion was in right subtree
        // Solution: Single left rotation
        if ($balance < -1 && $value > $node->right->data) {
            return $this->rotateLeft($node);
        }

        // Left-Right Case: Left subtree is taller but insertion was in right subtree of left child
        // Solution: Left rotation on left child, then right rotation on root
        if ($balance > 1 && $value > $node->left->data) {
            $node->left = $this->rotateLeft($node->left);
            return $this->rotateRight($node);
        }

        // Right-Left Case: Right subtree is taller but insertion was in left subtree of right child
        // Solution: Right rotation on right child, then left rotation on root
        if ($balance < -1 && $value < $node->right->data) {
            $node->right = $this->rotateRight($node->right);
            return $this->rotateLeft($node);
        }

        return $node;
    }

    // Find minimum value node
    private function minValueNode(AVLNode $node): AVLNode
    {
        $current = $node;
        while ($current->left !== null) {
            $current = $current->left;
        }
        return $current;
    }

    // Delete a value
    public function delete(mixed $value): void
    {
        $this->root = $this->deleteNode($this->root, $value);
    }

    private function deleteNode(?AVLNode $node, mixed $value): ?AVLNode
    {
        // Normal BST deletion
        if ($node === null) {
            return null;
        }

        if ($value < $node->data) {
            $node->left = $this->deleteNode($node->left, $value);
        } elseif ($value > $node->data) {
            $node->right = $this->deleteNode($node->right, $value);
        } else {
            // Node to be deleted found

            // Node with one child or no child
            if ($node->left === null) {
                return $node->right;
            } elseif ($node->right === null) {
                return $node->left;
            }

            // Node with two children: get inorder successor
            $successor = $this->minValueNode($node->right);
            $node->data = $successor->data;
            $node->right = $this->deleteNode($node->right, $successor->data);
        }

        // Update height
        $this->updateHeight($node);

        // Get balance factor
        $balance = $this->getBalance($node);

        // Left-Left Case
        if ($balance > 1 && $this->getBalance($node->left) >= 0) {
            return $this->rotateRight($node);
        }

        // Left-Right Case
        if ($balance > 1 && $this->getBalance($node->left) < 0) {
            $node->left = $this->rotateLeft($node->left);
            return $this->rotateRight($node);
        }

        // Right-Right Case
        if ($balance < -1 && $this->getBalance($node->right) <= 0) {
            return $this->rotateLeft($node);
        }

        // Right-Left Case
        if ($balance < -1 && $this->getBalance($node->right) > 0) {
            $node->right = $this->rotateRight($node->right);
            return $this->rotateLeft($node);
        }

        return $node;
    }

    // Search for a value
    public function search(mixed $value): bool
    {
        return $this->searchNode($this->root, $value);
    }

    private function searchNode(?AVLNode $node, mixed $value): bool
    {
        if ($node === null) {
            return false;
        }

        if ($value === $node->data) {
            return true;
        }

        if ($value < $node->data) {
            return $this->searchNode($node->left, $value);
        }

        return $this->searchNode($node->right, $value);
    }

    // In-order traversal
    public function inOrder(): array
    {
        $result = [];
        $this->inOrderTraversal($this->root, $result);
        return $result;
    }

    private function inOrderTraversal(?AVLNode $node, array &$result): void
    {
        if ($node === null) {
            return;
        }

        $this->inOrderTraversal($node->left, $result);
        $result[] = $node->data;
        $this->inOrderTraversal($node->right, $result);
    }

    // Visualize tree structure
    public function visualize(): void
    {
        $this->printTree($this->root, '', true);
    }

    private function printTree(?AVLNode $node, string $prefix, bool $isRight): void
    {
        if ($node === null) {
            return;
        }

        echo $prefix;
        echo $isRight ? '└── ' : '├── ';
        echo "{$node->data} (h:{$node->height}, bf:{$this->getBalance($node)})\n";

        $newPrefix = $prefix . ($isRight ? '    ' : '│   ');
        if ($node->left !== null || $node->right !== null) {
            $this->printTree($node->right, $newPrefix, false);
            $this->printTree($node->left, $newPrefix, true);
        }
    }
}

// Example usage
$avl = new AVLTree();
foreach ([10, 20, 30, 40, 50, 25] as $value) {
    $avl->insert($value);
}

$avl->visualize();
// Output shows balanced tree:
//         30 (h:3, bf:0)
//         ├── 40 (h:2, bf:-1)
//         │   └── 50 (h:1, bf:0)
//         └── 20 (h:2, bf:0)
//             ├── 25 (h:1, bf:0)
//             └── 10 (h:1, bf:0)

print_r($avl->inOrder());  // [10, 20, 25, 30, 40, 50]
echo $avl->search(25) ? 'Found' : 'Not found';  // Found

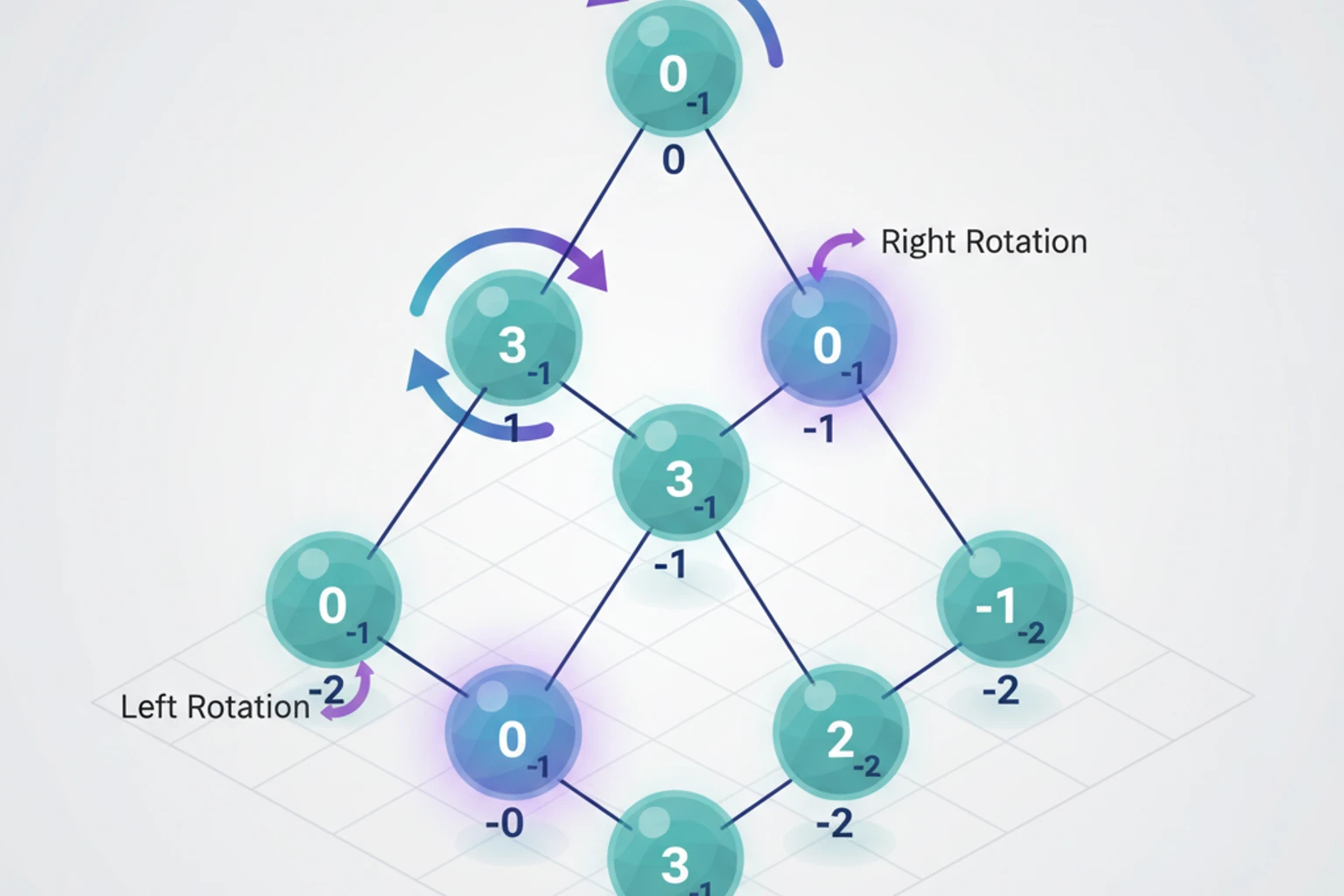
$avl->delete(30);
$avl->visualize();

AVL Tree Rotations

Four Cases Requiring Rebalancing

<?php

declare(strict_types=1);

class AVLTreeRotations
{
    // Case 1: Left-Left (Single Right Rotation)
    //       z                      y
    //      / \                    / \
    //     y   D    =>            x   z
    //    / \                    /   / \
    //   x   C                  A   C   D
    //  /
    // A
    public function leftLeftCase(): void
    {
        // Insert into left subtree of left child
        // Solution: Single right rotation at z
        echo "Left-Left Case: Single right rotation\n";
    }

    // Case 2: Right-Right (Single Left Rotation)
    //   z                          y
    //  / \                        / \
    // A   y        =>            z   x
    //    / \                    / \   \
    //   B   x                  A   B   D
    //        \
    //         D
    public function rightRightCase(): void
    {
        // Insert into right subtree of right child
        // Solution: Single left rotation at z
        echo "Right-Right Case: Single left rotation\n";
    }

    // Case 3: Left-Right (Double Rotation: Left then Right)
    //     z                    z                    x
    //    / \                  / \                  / \
    //   y   D    =>          x   D    =>          y   z
    //  / \                  / \                  /   / \
    // A   x                y   C                A   C   D
    //    /                /
    //   C                A
    public function leftRightCase(): void
    {
        // Insert into right subtree of left child
        // Solution: Left rotation at y, then right rotation at z
        echo "Left-Right Case: Double rotation (L-R)\n";
    }

    // Case 4: Right-Left (Double Rotation: Right then Left)
    //   z                    z                      x
    //  / \                  / \                    / \
    // A   y    =>          A   x        =>        z   y
    //    / \                  / \                / \   \
    //   x   D                B   y              A   B   D
    //    \                      /
    //     B                    D
    public function rightLeftCase(): void
    {
        // Insert into left subtree of right child
        // Solution: Right rotation at y, then left rotation at z
        echo "Right-Left Case: Double rotation (R-L)\n";
    }
}

Red-Black Trees

Red-Black trees are self-balancing binary search trees with less strict balancing than AVL trees, using node colors to maintain balance. While AVL trees maintain strict height balance, Red-Black trees maintain a looser form of balance through color properties, which allows them to perform fewer rotations during insertions and deletions. This makes Red-Black trees more efficient for write-heavy workloads, though searches may be slightly slower due to the taller trees (height bounded by 2 * log₂(n) vs AVL’s 1.44 * log₂(n)).

Red-Black Tree Properties

Red-Black trees maintain balance through five invariants:

Every node is either red or black — Each node has a color property
Root is always black — Ensures the first property can be maintained
All leaves (NULL/NIL) are black — Sentinel nodes are considered black
Red nodes have black children — No two red nodes can be adjacent (prevents long red chains)
All paths from root to leaves have the same number of black nodes — This “black height” property ensures balance

Why these properties work: Property 5 ensures that the longest path (alternating red-black) is at most twice the shortest path (all black), keeping the tree height logarithmic. Properties 3 and 4 prevent the tree from becoming too unbalanced by limiting consecutive red nodes.

Red-Black Node Implementation

<?php

declare(strict_types=1);

enum NodeColor: string
{
    case RED = 'red';
    case BLACK = 'black';
}

class RBNode
{
    public function __construct(
        public mixed $data,
        public NodeColor $color = NodeColor::RED,
        public ?RBNode $left = null,
        public ?RBNode $right = null,
        public ?RBNode $parent = null
    ) {}
}

class RedBlackTree
{
    private ?RBNode $root = null;
    private RBNode $nil;  // Sentinel node for leaves

    public function __construct()
    {
        // NIL node is always black
        $this->nil = new RBNode(null, NodeColor::BLACK);
        $this->root = $this->nil;
    }

    // Left rotation
    private function rotateLeft(RBNode $x): void
    {
        $y = $x->right;
        $x->right = $y->left;

        if ($y->left !== $this->nil) {
            $y->left->parent = $x;
        }

        $y->parent = $x->parent;

        if ($x->parent === null) {
            $this->root = $y;
        } elseif ($x === $x->parent->left) {
            $x->parent->left = $y;
        } else {
            $x->parent->right = $y;
        }

        $y->left = $x;
        $x->parent = $y;
    }

    // Right rotation
    private function rotateRight(RBNode $y): void
    {
        $x = $y->left;
        $y->left = $x->right;

        if ($x->right !== $this->nil) {
            $x->right->parent = $y;
        }

        $x->parent = $y->parent;

        if ($y->parent === null) {
            $this->root = $x;
        } elseif ($y === $y->parent->right) {
            $y->parent->right = $x;
        } else {
            $y->parent->left = $x;
        }

        $x->right = $y;
        $y->parent = $x;
    }

    // Insert a value
    public function insert(mixed $value): void
    {
        $node = new RBNode($value, NodeColor::RED, $this->nil, $this->nil);

        $parent = null;
        $current = $this->root;

        // Find position for new node
        while ($current !== $this->nil) {
            $parent = $current;
            if ($value < $current->data) {
                $current = $current->left;
            } else {
                $current = $current->right;
            }
        }

        $node->parent = $parent;

        // Insert node
        if ($parent === null) {
            $this->root = $node;
        } elseif ($value < $parent->data) {
            $parent->left = $node;
        } else {
            $parent->right = $node;
        }

        // Fix Red-Black properties
        $this->insertFixup($node);
    }

    // Fix Red-Black tree properties after insertion
    // New nodes are inserted as RED, which may violate property 4 (red nodes must have black children)
    // This function fixes violations by recoloring and rotating
    private function insertFixup(RBNode $z): void
    {
        // Continue fixing while parent is red (violation of property 4)
        while ($z->parent !== null && $z->parent->color === NodeColor::RED) {
            if ($z->parent === $z->parent->parent?->left) {
                $y = $z->parent->parent->right;  // Uncle

                if ($y->color === NodeColor::RED) {
                    // Case 1: Uncle is red
                    $z->parent->color = NodeColor::BLACK;
                    $y->color = NodeColor::BLACK;
                    $z->parent->parent->color = NodeColor::RED;
                    $z = $z->parent->parent;
                } else {
                    if ($z === $z->parent->right) {
                        // Case 2: Uncle is black, z is right child
                        $z = $z->parent;
                        $this->rotateLeft($z);
                    }
                    // Case 3: Uncle is black, z is left child
                    $z->parent->color = NodeColor::BLACK;
                    $z->parent->parent->color = NodeColor::RED;
                    $this->rotateRight($z->parent->parent);
                }
            } else {
                // Mirror cases
                $y = $z->parent->parent?->left;  // Uncle

                if ($y !== null && $y->color === NodeColor::RED) {
                    $z->parent->color = NodeColor::BLACK;
                    $y->color = NodeColor::BLACK;
                    $z->parent->parent->color = NodeColor::RED;
                    $z = $z->parent->parent;
                } else {
                    if ($z === $z->parent->left) {
                        $z = $z->parent;
                        $this->rotateRight($z);
                    }
                    $z->parent->color = NodeColor::BLACK;
                    if ($z->parent->parent !== null) {
                        $z->parent->parent->color = NodeColor::RED;
                        $this->rotateLeft($z->parent->parent);
                    }
                }
            }
        }

        $this->root->color = NodeColor::BLACK;
    }

    // Search for a value
    public function search(mixed $value): bool
    {
        return $this->searchNode($this->root, $value);
    }

    private function searchNode(?RBNode $node, mixed $value): bool
    {
        if ($node === null || $node === $this->nil) {
            return false;
        }

        if ($value === $node->data) {
            return true;
        }

        if ($value < $node->data) {
            return $this->searchNode($node->left, $value);
        }

        return $this->searchNode($node->right, $value);
    }

    // Find minimum node
    private function minimum(RBNode $node): RBNode
    {
        while ($node->left !== $this->nil) {
            $node = $node->left;
        }
        return $node;
    }

    // Transplant subtree
    private function transplant(RBNode $u, RBNode $v): void
    {
        if ($u->parent === null) {
            $this->root = $v;
        } elseif ($u === $u->parent->left) {
            $u->parent->left = $v;
        } else {
            $u->parent->right = $v;
        }
        $v->parent = $u->parent;
    }

    // Delete a value
    public function delete(mixed $value): void
    {
        $z = $this->findNode($this->root, $value);
        if ($z === $this->nil) {
            return;  // Value not found
        }

        $y = $z;
        $yOriginalColor = $y->color;

        if ($z->left === $this->nil) {
            $x = $z->right;
            $this->transplant($z, $z->right);
        } elseif ($z->right === $this->nil) {
            $x = $z->left;
            $this->transplant($z, $z->left);
        } else {
            $y = $this->minimum($z->right);
            $yOriginalColor = $y->color;
            $x = $y->right;

            if ($y->parent === $z) {
                $x->parent = $y;
            } else {
                $this->transplant($y, $y->right);
                $y->right = $z->right;
                $y->right->parent = $y;
            }

            $this->transplant($z, $y);
            $y->left = $z->left;
            $y->left->parent = $y;
            $y->color = $z->color;
        }

        if ($yOriginalColor === NodeColor::BLACK) {
            $this->deleteFixup($x);
        }
    }

    // Find node with given value
    private function findNode(RBNode $node, mixed $value): RBNode
    {
        while ($node !== $this->nil && $value !== $node->data) {
            if ($value < $node->data) {
                $node = $node->left;
            } else {
                $node = $node->right;
            }
        }
        return $node;
    }

    // Fix Red-Black tree properties after deletion
    private function deleteFixup(RBNode $x): void
    {
        while ($x !== $this->root && $x->color === NodeColor::BLACK) {
            if ($x === $x->parent?->left) {
                $w = $x->parent->right;

                if ($w->color === NodeColor::RED) {
                    $w->color = NodeColor::BLACK;
                    $x->parent->color = NodeColor::RED;
                    $this->rotateLeft($x->parent);
                    $w = $x->parent->right;
                }

                if ($w->left->color === NodeColor::BLACK &&
                    $w->right->color === NodeColor::BLACK) {
                    $w->color = NodeColor::RED;
                    $x = $x->parent;
                } else {
                    if ($w->right->color === NodeColor::BLACK) {
                        $w->left->color = NodeColor::BLACK;
                        $w->color = NodeColor::RED;
                        $this->rotateRight($w);
                        $w = $x->parent->right;
                    }
                    $w->color = $x->parent->color;
                    $x->parent->color = NodeColor::BLACK;
                    $w->right->color = NodeColor::BLACK;
                    $this->rotateLeft($x->parent);
                    $x = $this->root;
                }
            } else {
                // Mirror cases
                $w = $x->parent?->left;

                if ($w !== null && $w->color === NodeColor::RED) {
                    $w->color = NodeColor::BLACK;
                    $x->parent->color = NodeColor::RED;
                    $this->rotateRight($x->parent);
                    $w = $x->parent->left;
                }

                if ($w !== null &&
                    $w->right->color === NodeColor::BLACK &&
                    $w->left->color === NodeColor::BLACK) {
                    $w->color = NodeColor::RED;
                    $x = $x->parent;
                } else {
                    if ($w !== null && $w->left->color === NodeColor::BLACK) {
                        $w->right->color = NodeColor::BLACK;
                        $w->color = NodeColor::RED;
                        $this->rotateLeft($w);
                        $w = $x->parent->left;
                    }
                    if ($w !== null) {
                        $w->color = $x->parent->color;
                        $x->parent->color = NodeColor::BLACK;
                        $w->left->color = NodeColor::BLACK;
                        $this->rotateRight($x->parent);
                    }
                    $x = $this->root;
                }
            }
        }
        $x->color = NodeColor::BLACK;
    }

    // In-order traversal
    public function inOrder(): array
    {
        $result = [];
        $this->inOrderTraversal($this->root, $result);
        return $result;
    }

    private function inOrderTraversal(RBNode $node, array &$result): void
    {
        if ($node === $this->nil) {
            return;
        }

        $this->inOrderTraversal($node->left, $result);
        $result[] = [
            'value' => $node->data,
            'color' => $node->color->value
        ];
        $this->inOrderTraversal($node->right, $result);
    }
}

// Example usage
$rbt = new RedBlackTree();
foreach ([10, 20, 30, 15, 25, 5] as $value) {
    $rbt->insert($value);
}

print_r($rbt->inOrder());
echo $rbt->search(15) ? 'Found' : 'Not found';  // Found

$rbt->delete(15);
print_r($rbt->inOrder());

Real-World Usage Examples

Balanced trees are used extensively in real-world systems. Here are some concrete examples:

1. Linux Kernel

The Linux kernel uses Red-Black trees extensively for:

Process scheduling: Managing run queues and process priorities
Virtual memory management: Tracking memory regions
File system: Directory entries and inode caches
Network routing: IP routing tables

Why Red-Black? The kernel needs fast insertions/deletions (write-heavy) and Red-Black trees provide better write performance than AVL trees.

2. Java Collections Framework

Java TreeMap and TreeSet use Red-Black trees internally:

TreeMap<K, V>: Sorted key-value pairs
TreeSet<E>: Sorted set implementation

// Java TreeMap uses Red-Black tree internally
TreeMap<Integer, String> map = new TreeMap<>();
map.put(10, "ten");
map.put(20, "twenty");
// Guarantees O(log n) for all operations

Why Red-Black? Java prioritizes consistent performance for insertions and deletions, which Red-Black trees provide.

3. C++ Standard Library

C++ std::map and std::set typically use Red-Black trees:

std::map<K, V>: Ordered associative container
std::set<T>: Ordered set container

Why Red-Black? C++ standard doesn’t mandate implementation, but most implementations (GCC, Clang) use Red-Black trees for their balanced performance characteristics.

4. Database Systems

PostgreSQL uses both AVL and Red-Black trees:

AVL trees: For read-heavy indexes where search performance is critical
Red-Black trees: For write-heavy indexes and internal data structures

MySQL InnoDB uses B+ trees (a variant of B-trees) for indexes, but the concepts are similar.

5. PHP Internal Usage

While PHP doesn’t expose balanced trees directly, the concepts apply to:

SPL Data Structures: SplHeap, SplPriorityQueue use heap structures (similar balancing concepts)
Array sorting: Internal sorting algorithms use balanced tree concepts
Session storage: Some session handlers use tree structures for efficient lookups

AVL vs Red-Black Trees Comparison

<?php

declare(strict_types=1);

class TreeComparison
{
    public function compareCharacteristics(): array
    {
        return [
            'Balance' => [
                'AVL' => 'Strictly balanced (height diff ≤ 1)',
                'Red-Black' => 'Loosely balanced (black-height equality)'
            ],
            'Height' => [
                'AVL' => '~1.44 * log(n) (tighter)',
                'Red-Black' => '~2 * log(n) (looser)'
            ],
            'Insertion' => [
                'AVL' => 'Slower (more rotations)',
                'Red-Black' => 'Faster (fewer rotations, max 2)'
            ],
            'Deletion' => [
                'AVL' => 'Slower (more rotations)',
                'Red-Black' => 'Faster (fewer rotations, max 3)'
            ],
            'Search' => [
                'AVL' => 'Faster (better balanced)',
                'Red-Black' => 'Slightly slower'
            ],
            'Memory' => [
                'AVL' => 'Height field per node',
                'Red-Black' => 'Color bit per node'
            ],
            'Use Case' => [
                'AVL' => 'Read-heavy workloads',
                'Red-Black' => 'Write-heavy workloads'
            ],
            'Real-World Usage' => [
                'AVL' => 'Database indexes (read-heavy), search engines',
                'Red-Black' => 'Linux kernel, Java TreeMap, C++ std::map'
            ]
        ];
    }

    public function benchmark(int $operations = 10000): array
    {
        $results = [];

        // AVL Tree benchmark
        $avl = new AVLTree();
        $avlInsertTime = microtime(true);
        for ($i = 0; $i < $operations; $i++) {
            $avl->insert(random_int(1, $operations * 10));
        }
        $avlInsertTime = microtime(true) - $avlInsertTime;

        $avlSearchTime = microtime(true);
        for ($i = 0; $i < $operations / 10; $i++) {
            $avl->search(random_int(1, $operations * 10));
        }
        $avlSearchTime = microtime(true) - $avlSearchTime;

        // Red-Black Tree benchmark
        $rbt = new RedBlackTree();
        $rbtInsertTime = microtime(true);
        for ($i = 0; $i < $operations; $i++) {
            $rbt->insert(random_int(1, $operations * 10));
        }
        $rbtInsertTime = microtime(true) - $rbtInsertTime;

        $rbtSearchTime = microtime(true);
        for ($i = 0; $i < $operations / 10; $i++) {
            $rbt->search(random_int(1, $operations * 10));
        }
        $rbtSearchTime = microtime(true) - $rbtSearchTime;

        $results = [
            'operations' => $operations,
            'avl' => [
                'insert_time_ms' => round($avlInsertTime * 1000, 2),
                'search_time_ms' => round($avlSearchTime * 1000, 2),
                'insert_per_op' => round($avlInsertTime / $operations * 1000000, 3) . ' μs',
                'search_per_op' => round($avlSearchTime / ($operations / 10) * 1000000, 3) . ' μs',
            ],
            'red_black' => [
                'insert_time_ms' => round($rbtInsertTime * 1000, 2),
                'search_time_ms' => round($rbtSearchTime * 1000, 2),
                'insert_per_op' => round($rbtInsertTime / $operations * 1000000, 3) . ' μs',
                'search_per_op' => round($rbtSearchTime / ($operations / 10) * 1000000, 3) . ' μs',
            ],
            'analysis' => [
                'insert_winner' => $rbtInsertTime < $avlInsertTime ? 'Red-Black' : 'AVL',
                'insert_diff' => round(abs($rbtInsertTime - $avlInsertTime) / max($avlInsertTime, $rbtInsertTime) * 100, 1) . '%',
                'search_winner' => $avlSearchTime < $rbtSearchTime ? 'AVL' : 'Red-Black',
                'search_diff' => round(abs($rbtSearchTime - $avlSearchTime) / max($avlSearchTime, $rbtSearchTime) * 100, 1) . '%',
            ]
        ];

        return $results;
    }

    public function printBenchmarkResults(int $operations = 10000): void
    {
        $results = $this->benchmark($operations);

        echo "Performance Comparison ({$results['operations']} operations):\n\n";
        echo "AVL Tree:\n";
        echo "  Insert: {$results['avl']['insert_time_ms']} ms ({$results['avl']['insert_per_op']} per operation)\n";
        echo "  Search: {$results['avl']['search_time_ms']} ms ({$results['avl']['search_per_op']} per operation)\n\n";
        echo "Red-Black Tree:\n";
        echo "  Insert: {$results['red_black']['insert_time_ms']} ms ({$results['red_black']['insert_per_op']} per operation)\n";
        echo "  Search: {$results['red_black']['search_time_ms']} ms ({$results['red_black']['search_per_op']} per operation)\n\n";
        echo "Analysis:\n";
        echo "  Insert Winner: {$results['analysis']['insert_winner']} ({$results['analysis']['insert_diff']} difference)\n";
        echo "  Search Winner: {$results['analysis']['search_winner']} ({$results['analysis']['search_diff']} difference)\n";
        echo "\nConclusion: ";
        if ($results['analysis']['insert_winner'] === 'Red-Black' && $results['analysis']['search_winner'] === 'AVL') {
            echo "Red-Black is faster for writes, AVL is faster for reads (as expected)\n";
        }
    }
}

// Example usage
$comparison = new TreeComparison();
$comparison->printBenchmarkResults(10000);

// Typical output:
// Performance Comparison (10000 operations):
//
// AVL Tree:
//   Insert: 45.23 ms (4.523 μs per operation)
//   Search: 2.15 ms (0.215 μs per operation)
//
// Red-Black Tree:
//   Insert: 38.67 ms (3.867 μs per operation)
//   Search: 2.34 ms (0.234 μs per operation)
//
// Analysis:
//   Insert Winner: Red-Black (14.5% difference)
//   Search Winner: AVL (8.8% difference)
//
// Conclusion: Red-Black is faster for writes, AVL is faster for reads (as expected)

Complexity Analysis

AVL Trees

Operation	Average	Worst Case	Notes
Search	O(log n)	O(log n)	Height bounded by 1.44 * log(n)
Insert	O(log n)	O(log n)	May require rotations
Delete	O(log n)	O(log n)	May require rotations
Space	O(n)	O(n)	Height field per node

Red-Black Trees

Operation	Average	Worst Case	Notes
Search	O(log n)	O(log n)	Height bounded by 2 * log(n)
Insert	O(log n)	O(log n)	Max 2 rotations
Delete	O(log n)	O(log n)	Max 3 rotations
Space	O(n)	O(n)	Color bit per node

Tree Augmentation: Order Statistics

Tree augmentation allows us to store additional information in each node to support advanced queries efficiently. One common augmentation is storing subtree sizes, which enables order statistics queries like finding the kth smallest element or the rank of an element in O(log n) time.

Augmented AVL Node

<?php

declare(strict_types=1);

class AugmentedAVLNode
{
    public function __construct(
        public mixed $data,
        public ?AugmentedAVLNode $left = null,
        public ?AugmentedAVLNode $right = null,
        public int $height = 1,
        public int $size = 1  // Number of nodes in subtree rooted at this node
    ) {}
}

class OrderStatisticsTree
{
    private ?AugmentedAVLNode $root = null;

    private function height(?AugmentedAVLNode $node): int
    {
        return $node?->height ?? 0;
    }

    private function size(?AugmentedAVLNode $node): int
    {
        return $node?->size ?? 0;
    }

    private function updateNodeInfo(AugmentedAVLNode $node): void
    {
        $node->height = 1 + max(
            $this->height($node->left),
            $this->height($node->right)
        );
        $node->size = 1 + $this->size($node->left) + $this->size($node->right);
    }

    private function getBalance(?AugmentedAVLNode $node): int
    {
        if ($node === null) {
            return 0;
        }
        return $this->height($node->left) - $this->height($node->right);
    }

    private function rotateRight(AugmentedAVLNode $y): AugmentedAVLNode
    {
        $x = $y->left;
        $B = $x->right;

        $x->right = $y;
        $y->left = $B;

        // Update sizes and heights (must update y first, then x)
        $this->updateNodeInfo($y);
        $this->updateNodeInfo($x);

        return $x;
    }

    private function rotateLeft(AugmentedAVLNode $x): AugmentedAVLNode
    {
        $y = $x->right;
        $B = $y->left;

        $y->left = $x;
        $x->right = $B;

        // Update sizes and heights
        $this->updateNodeInfo($x);
        $this->updateNodeInfo($y);

        return $y;
    }

    public function insert(mixed $value): void
    {
        $this->root = $this->insertNode($this->root, $value);
    }

    private function insertNode(?AugmentedAVLNode $node, mixed $value): AugmentedAVLNode
    {
        if ($node === null) {
            return new AugmentedAVLNode($value);
        }

        if ($value < $node->data) {
            $node->left = $this->insertNode($node->left, $value);
        } elseif ($value > $node->data) {
            $node->right = $this->insertNode($node->right, $value);
        } else {
            return $node;  // Duplicate
        }

        // Update size and height
        $this->updateNodeInfo($node);

        // Rebalance
        $balance = $this->getBalance($node);

        if ($balance > 1 && $value < $node->left->data) {
            return $this->rotateRight($node);
        }
        if ($balance < -1 && $value > $node->right->data) {
            return $this->rotateLeft($node);
        }
        if ($balance > 1 && $value > $node->left->data) {
            $node->left = $this->rotateLeft($node->left);
            return $this->rotateRight($node);
        }
        if ($balance < -1 && $value < $node->right->data) {
            $node->right = $this->rotateRight($node->right);
            return $this->rotateLeft($node);
        }

        return $node;
    }

    // Find kth smallest element (1-indexed)
    public function findKthSmallest(int $k): ?mixed
    {
        if ($k < 1 || $k > $this->size($this->root)) {
            return null;
        }
        return $this->findKthSmallestNode($this->root, $k);
    }

    private function findKthSmallestNode(?AugmentedAVLNode $node, int $k): ?mixed
    {
        if ($node === null) {
            return null;
        }

        $leftSize = $this->size($node->left);

        if ($k <= $leftSize) {
            // kth smallest is in left subtree
            return $this->findKthSmallestNode($node->left, $k);
        } elseif ($k === $leftSize + 1) {
            // Current node is the kth smallest
            return $node->data;
        } else {
            // kth smallest is in right subtree
            return $this->findKthSmallestNode($node->right, $k - $leftSize - 1);
        }
    }

    // Find rank of an element (1-indexed: position in sorted order)
    public function rank(mixed $value): int
    {
        return $this->rankNode($this->root, $value);
    }

    private function rankNode(?AugmentedAVLNode $node, mixed $value): int
    {
        if ($node === null) {
            return 0;
        }

        if ($value < $node->data) {
            return $this->rankNode($node->left, $value);
        } elseif ($value === $node->data) {
            return $this->size($node->left) + 1;
        } else {
            return $this->size($node->left) + 1 + $this->rankNode($node->right, $value);
        }
    }

    // Count elements in range [start, end]
    public function rangeCount(mixed $start, mixed $end): int
    {
        return $this->rank($end) - $this->rank($start) + ($this->search($start) ? 1 : 0);
    }

    public function search(mixed $value): bool
    {
        return $this->searchNode($this->root, $value);
    }

    private function searchNode(?AugmentedAVLNode $node, mixed $value): bool
    {
        if ($node === null) {
            return false;
        }
        if ($value === $node->data) {
            return true;
        }
        if ($value < $node->data) {
            return $this->searchNode($node->left, $value);
        }
        return $this->searchNode($node->right, $value);
    }
}

// Example usage
$ost = new OrderStatisticsTree();
foreach ([10, 20, 30, 40, 50, 25, 35] as $value) {
    $ost->insert($value);
}

echo $ost->findKthSmallest(3) . "\n";  // 25 (3rd smallest)
echo $ost->findKthSmallest(5) . "\n";  // 35 (5th smallest)
echo $ost->rank(30) . "\n";             // 4 (30 is 4th smallest)
echo $ost->rangeCount(20, 40) . "\n";  // 4 (20, 25, 30, 35)

Why It Works: By storing subtree sizes, we can determine how many elements are smaller than the current node. When searching for the kth smallest:

If k ≤ left subtree size, the kth element is in the left subtree
If k = left subtree size + 1, the current node is the kth element
Otherwise, the kth element is in the right subtree at position (k - left size - 1)

The key is maintaining subtree sizes correctly during rotations. When rotating, we must recalculate sizes for affected nodes, which is why updateNodeInfo() updates both height and size.

Practical Applications

1. In-Memory Databases

<?php

declare(strict_types=1);

class OrderedIndex
{
    private AVLTree $index;

    public function __construct()
    {
        $this->index = new AVLTree();
    }

    public function addRecord(int $id, array $data): void
    {
        $this->index->insert($id);
        // Store actual data elsewhere, indexed by id
    }

    public function findRecord(int $id): bool
    {
        return $this->index->search($id);
    }

    public function rangeQuery(int $start, int $end): array
    {
        // Get all records in sorted order, filter by range
        $allRecords = $this->index->inOrder();
        return array_filter($allRecords, fn($id) => $id >= $start && $id <= $end);
    }
}

2. PHP’s Internal Implementation

<?php

declare(strict_types=1);

// PHP's SPL (Standard PHP Library) doesn't expose AVL/RB tree directly,
// but you can use SplHeap or implement custom sorted structures

class SortedSet
{
    private AVLTree $tree;

    public function __construct()
    {
        $this->tree = new AVLTree();
    }

    public function add(mixed $value): void
    {
        $this->tree->insert($value);
    }

    public function contains(mixed $value): bool
    {
        return $this->tree->search($value);
    }

    public function toArray(): array
    {
        return $this->tree->inOrder();
    }

    public function first(): mixed
    {
        $values = $this->tree->inOrder();
        return $values[0] ?? null;
    }

    public function last(): mixed
    {
        $values = $this->tree->inOrder();
        return end($values) ?: null;
    }
}

// Usage
$set = new SortedSet();
$set->add(5);
$set->add(2);
$set->add(8);
$set->add(1);

print_r($set->toArray());  // [1, 2, 5, 8] - always sorted
echo $set->first();        // 1
echo $set->last();         // 8

3. Priority Queue with Updates

<?php

declare(strict_types=1);

class UpdatablePriorityQueue
{
    private RedBlackTree $tree;
    private array $positions = [];  // Track node positions for updates

    public function __construct()
    {
        $this->tree = new RedBlackTree();
    }

    public function insert(string $id, int $priority): void
    {
        $this->tree->insert($priority);
        $this->positions[$id] = $priority;
    }

    public function updatePriority(string $id, int $newPriority): void
    {
        if (isset($this->positions[$id])) {
            $oldPriority = $this->positions[$id];
            $this->tree->delete($oldPriority);
            $this->tree->insert($newPriority);
            $this->positions[$id] = $newPriority;
        }
    }

    public function extractMin(): ?string
    {
        $values = $this->tree->inOrder();
        if (empty($values)) {
            return null;
        }

        $minPriority = $values[0]['value'];
        $minId = array_search($minPriority, $this->positions);

        $this->tree->delete($minPriority);
        unset($this->positions[$minId]);

        return $minId;
    }
}

Best Practices

Choose the Right Tree
- Use AVL for read-heavy workloads (databases, dictionaries)
- Use Red-Black for write-heavy workloads (system libraries)
- Consider memory constraints (color bit vs height field)
Implementation Tips
- Always maintain tree properties during modifications
- Use sentinel nodes (NIL) in Red-Black trees to simplify logic
- Test thoroughly with edge cases (single node, deletions, duplicates)
When to Use
- Need guaranteed O(log n) operations
- Cannot tolerate worst-case O(n) of regular BST
- Require sorted data with frequent updates
When Not to Use
- Small datasets (overhead not worth it)
- Hash table would work (O(1) average, no ordering needed)
- Data is append-only (B-tree might be better)

Troubleshooting

Error: “Call to a member function on null”

Symptom: Fatal error: Uncaught Error: Call to a member function data on null

Cause: Accessing left or right child without checking if it’s null first, especially in rotation operations.

Solution: Always check for null before accessing node properties:

// Wrong
if ($balance > 1 && $value < $node->left->data) {  // May fail if left is null
    return $this->rotateRight($node);
}

// Correct
if ($balance > 1 && $node->left !== null && $value < $node->left->data) {
    return $this->rotateRight($node);
}

Error: “Tree becomes unbalanced after deletion”

Symptom: Tree balance factors exceed [-1, 0, 1] after deletion operations.

Cause: Not rebalancing after deletion, or incorrect rotation case detection.

Solution: Ensure deletion rebalancing checks all four cases and updates heights:

// After deletion, always check balance and rebalance
$this->updateHeight($node);
$balance = $this->getBalance($node);

// Check all four rotation cases
if ($balance > 1 && $this->getBalance($node->left) >= 0) {
    return $this->rotateRight($node);
}
// ... other cases

Problem: Red-Black tree violates color properties

Symptom: Two red nodes appear consecutively, or black height is inconsistent.

Cause: Not properly fixing violations in insertFixup or deleteFixup, or missing null checks for parent nodes.

Solution: Ensure fixup functions handle all cases and check for null parents:

// Always check parent exists before accessing
while ($z->parent !== null && $z->parent->color === NodeColor::RED) {
    if ($z->parent->parent !== null) {
        // Safe to access grandparent
        $y = $z->parent->parent->right;
        // ... rest of fixup logic
    }
}

Problem: Height not updating correctly

Symptom: Balance factors are incorrect, leading to unnecessary rotations or missed rebalancing.

Cause: Not updating heights after rotations, or updating in wrong order.

Solution: Always update heights after structural changes, and update child before parent:

// Correct order: update children first, then parent
$this->updateHeight($y);  // Child first
$this->updateHeight($x);  // Parent second

Problem: Sentinel node (NIL) causing issues

Symptom: Red-Black tree operations fail with null pointer errors.

Cause: Not properly initializing NIL node or not checking for NIL in comparisons.

Solution: Initialize NIL in constructor and always use === $this->nil for comparisons:

public function __construct()
{
    $this->nil = new RBNode(null, NodeColor::BLACK);
    $this->root = $this->nil;
}

// Always check against NIL properly
if ($node === $this->nil) {
    return;  // Not: if ($node === null)
}

Practice Exercises

Exercise 1: Validate AVL Balance

Goal: Verify that an AVL tree maintains proper balance factors

Write a function that checks if an AVL tree is properly balanced:

function isAVLBalanced(?AVLNode $node): bool
{
    // Your code here
    // Check that balance factor is -1, 0, or 1 for all nodes
    // Recursively check left and right subtrees
}

Validation: Test with a balanced and unbalanced tree:

$avl = new AVLTree();
$avl->insert(10);
$avl->insert(20);
$avl->insert(30);

echo isAVLBalanced($avl->root) ? 'Balanced' : 'Unbalanced';
// Expected: Balanced (tree should auto-balance)

Exercise 2: Validate Red-Black Properties

Goal: Verify Red-Black tree properties are maintained

Write a function that checks all five Red-Black tree properties:

function isValidRedBlack(?RBNode $root, RBNode $nil): bool
{
    // Your code here
    // Check: 1) Root is black, 2) No red-red violations,
    // 3) Black height is consistent, 4) Leaves are black
}

Validation: Test with a valid and invalid Red-Black tree.

Exercise 3: Range Count Query

Goal: Count nodes in a range efficiently

Implement a method to count nodes with values in range [a, b] in O(log n + k) time where k is the number of nodes in range. You can use the augmented tree approach from the Tree Augmentation section:

public function rangeCount(mixed $start, mixed $end): int
{
    // Your code here
    // Hint: Use rank() function: rank(end) - rank(start) + 1 if start exists
    // Or traverse and count nodes in range
}

Validation: Test with various ranges:

$ost = new OrderStatisticsTree();
foreach ([10, 20, 30, 40, 50, 25, 35] as $v) {
    $ost->insert($v);
}

echo $ost->rangeCount(20, 40);  // Expected: 4 (20, 25, 30, 35)
echo $ost->rangeCount(15, 45);  // Expected: 5 (20, 25, 30, 35, 40)

Exercise 4: Merge Two Balanced Trees

Goal: Combine two balanced trees efficiently

Merge two AVL or Red-Black trees into one balanced tree:

function mergeTrees(AVLTree $tree1, AVLTree $tree2): AVLTree
{
    // Your code here
    // Hint: Use in-order traversal to get sorted values,
    // then build a new balanced tree
}

Validation: Verify the merged tree is balanced and contains all elements.

Exercise 5: Kth Smallest Element

Goal: Find kth smallest element in O(log n) time

Implement the augmented tree approach shown in the Tree Augmentation section. The key is maintaining subtree sizes:

public function findKthSmallest(int $k): mixed
{
    // Your code here
    // Use the implementation from Tree Augmentation section
    // Remember to update subtree sizes during rotations
}

Validation: Test with various k values:

$ost = new OrderStatisticsTree();
foreach ([10, 20, 30, 40, 50] as $v) {
    $ost->insert($v);
}

echo $ost->findKthSmallest(1);  // Expected: 10
echo $ost->findKthSmallest(3);  // Expected: 30
echo $ost->findKthSmallest(5);  // Expected: 50
echo $ost->rank(30);            // Expected: 3 (30 is 3rd smallest)

Key Takeaways

Balanced trees maintain O(log n) height automatically through rotations
AVL trees are strictly balanced (height diff ≤ 1), better for searches
Red-Black trees are loosely balanced (black-height equality), better for updates
AVL requires more rotations (slower updates) but has tighter height bounds
Red-Black requires fewer rotations (max 2-3) but slightly taller trees
Choose based on workload: AVL for read-heavy, Red-Black for write-heavy
Both guarantee O(log n) worst-case for search, insert, delete
Tree augmentation enables advanced queries like order statistics in O(log n)
Subtree sizes can be maintained during rotations for kth smallest/rank queries
Real-world usage: Linux kernel (Red-Black), Java TreeMap (Red-Black), databases (both)
PHP doesn’t have built-in balanced trees, but concepts apply to many data structures
Understanding balanced trees is essential for database internals and system programming

💻 Code Samples

All code examples from this chapter are available in the GitHub repository:

View Chapter 20 Code Samples

Clone the repository to run examples:

git clone https://github.com/dalehurley/codewithphp.git
cd codewithphp/code/php-algorithms/chapter-20
php 01-*.php

What’s Next

In the next chapter, we’ll explore Graph Representations, learning how to model relationships and connections between entities using adjacency lists, adjacency matrices, and edge lists.

20: Balanced Trees: AVL & Red-Black Trees

20: Balanced Trees: AVL & Red-Black Trees Advanced

What You’ll Learn

Prerequisites

Overview

The Problem with Unbalanced Trees

AVL Trees

Balance Factor

AVL Node Implementation

AVL Tree Rotations

Four Cases Requiring Rebalancing

Red-Black Trees

Red-Black Tree Properties

Red-Black Node Implementation

Real-World Usage Examples

1. Linux Kernel

2. Java Collections Framework

3. C++ Standard Library

4. Database Systems

5. PHP Internal Usage

AVL vs Red-Black Trees Comparison

Complexity Analysis

AVL Trees

Red-Black Trees

Tree Augmentation: Order Statistics

Augmented AVL Node

Practical Applications

1. In-Memory Databases

2. PHP’s Internal Implementation

3. Priority Queue with Updates

Best Practices

Troubleshooting

Error: “Call to a member function on null”

Error: “Tree becomes unbalanced after deletion”

Problem: Red-Black tree violates color properties

Problem: Height not updating correctly

Problem: Sentinel node (NIL) causing issues

Practice Exercises

Exercise 1: Validate AVL Balance

Exercise 2: Validate Red-Black Properties

Exercise 3: Range Count Query

Exercise 4: Merge Two Balanced Trees

Exercise 5: Kth Smallest Element

Key Takeaways

Further Reading

💻 Code Samples

What’s Next