07: Quick Sort & Pivot Strategies

Quick Sort & Pivot Strategies Intermediate

Quick Sort is one of the most important and widely used sorting algorithms. Despite having O(n²) worst-case complexity, it’s typically faster than other O(n log n) algorithms in practice due to excellent cache locality and low overhead. In this chapter, we’ll master Quick Sort and learn how to optimize it with smart pivot selection.

What You’ll Learn

Estimated time: 65 minutes

By the end of this chapter, you will:

• Implement Quick Sort using the divide-and-conquer partitioning approach
• Master different pivot selection strategies (first, last, middle, random, median-of-three)
• Understand Quick Sort’s O(n log n) average case and O(n²) worst case scenarios
• Learn optimization techniques including tail recursion and hybrid approaches
• Apply Quick Sort to real-world scenarios and understand why it’s often faster than Merge Sort

Prerequisites

Before starting this chapter, ensure you have:

• ✓ Understanding of recursion (70 mins from Chapter 3 if not done)
• ✓ Understanding of Big O notation (60 mins from Chapter 1 if not done)
• ✓ Completion of Chapters 05-06 (115 mins if not done)

Quick Checklist

Complete these hands-on tasks as you work through the chapter:

• Implement basic Quick Sort with the partition function
• Try different pivot strategies: first element, last element, middle element
• Implement median-of-three pivot selection for better performance
• Add random pivot selection to avoid worst-case scenarios
• Benchmark Quick Sort against Merge Sort on various datasets
• Implement hybrid Quick Sort that switches to Insertion Sort for small subarrays
• (Optional) Implement three-way partitioning for handling duplicate elements

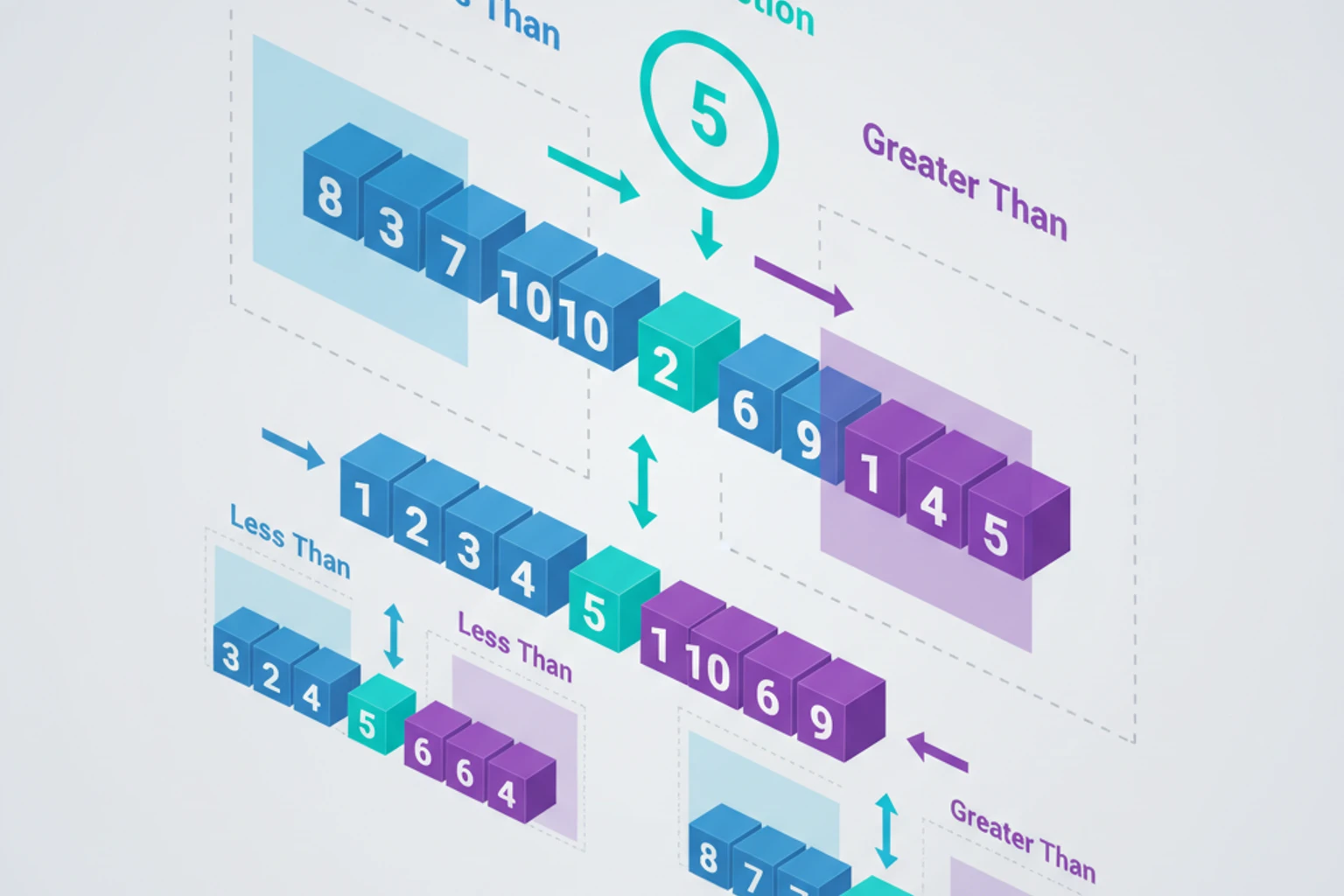
How Quick Sort Works

Quick Sort uses a divide-and-conquer strategy:

1. Pick a pivot element from the array
2. Partition the array so elements smaller than pivot are on the left, larger on the right
3. Recursively sort the left and right partitions

Key insight: After partitioning, the pivot is in its final sorted position!

Detailed Example with Step-by-Step Partition

Sort [8, 3, 1, 7, 0, 10, 2] using last element as pivot:

Initial Array: [8, 3, 1, 7, 0, 10, 2], pivot = 2

Partition Process:

i = -1 (tracks boundary of smaller elements)

j=0: arr[0]=8, 8 < 2? No → skip
     [8, 3, 1, 7, 0, 10, 2]  i=-1

j=1: arr[1]=3, 3 < 2? No → skip
     [8, 3, 1, 7, 0, 10, 2]  i=-1

j=2: arr[2]=1, 1 < 2? Yes → i++, swap arr[0] with arr[2]
     [1, 3, 8, 7, 0, 10, 2]  i=0

j=3: arr[3]=7, 7 < 2? No → skip
     [1, 3, 8, 7, 0, 10, 2]  i=0

j=4: arr[4]=0, 0 < 2? Yes → i++, swap arr[1] with arr[4]
     [1, 0, 8, 7, 3, 10, 2]  i=1

j=5: arr[5]=10, 10 < 2? No → skip
     [1, 0, 8, 7, 3, 10, 2]  i=1

Place pivot: swap arr[2] with pivot
     [1, 0, 2, 7, 3, 10, 8]  pivot at index 2

Result: All elements < 2 are on left, all > 2 are on right

Recursion:

• Left: [1, 0] → pivot=0 → [0, 1]
• Right: [7, 3, 10, 8] → pivot=8 → … → [3, 7, 8, 10]

Final: [0, 1, 2, 3, 7, 8, 10]

Animation Concept: Imagine a dividing wall moving through the array. Elements smaller than pivot jump over the wall to the left, while larger elements stay on the right. The pivot then slides into position at the wall.

Basic Implementation

function quickSort(array $arr): array
{
    // Base case: arrays with 0 or 1 element are already sorted
    if (count($arr) < 2) {
        return $arr;
    }

    // Choose pivot (simple: use first element)
    $pivot = $arr[0];
    $left = [];
    $right = [];

    // Partition: elements < pivot go left, >= pivot go right
    for ($i = 1; $i < count($arr); $i++) {
        if ($arr[$i] < $pivot) {
            $left[] = $arr[$i];
        } else {
            $right[] = $arr[$i];
        }
    }

    // Recursively sort and combine
    return array_merge(
        quickSort($left),
        [$pivot],
        quickSort($right)
    );
}

$numbers = [8, 3, 1, 7, 0, 10, 2];
print_r(quickSort($numbers));
// Output: [0, 1, 2, 3, 7, 8, 10]

Note: This implementation is easy to understand but not space-efficient (creates new arrays). Let’s build an in-place version.

In-Place Quick Sort

In-place sorting uses O(1) extra space by partitioning within the original array:

function quickSortInPlace(array &$arr, int $low = 0, int $high = null): void
{
    if ($high === null) {
        $high = count($arr) - 1;
    }

    if ($low < $high) {
        // Partition and get pivot index
        $pivotIndex = partition($arr, $low, $high);

        // Recursively sort left and right partitions
        quickSortInPlace($arr, $low, $pivotIndex - 1);
        quickSortInPlace($arr, $pivotIndex + 1, $high);
    }
}

function partition(array &$arr, int $low, int $high): int
{
    // Choose last element as pivot
    $pivot = $arr[$high];
    $i = $low - 1; // Index of smaller element

    for ($j = $low; $j < $high; $j++) {
        // If current element is smaller than pivot
        if ($arr[$j] < $pivot) {
            $i++;
            // Swap arr[i] and arr[j]
            [$arr[$i], $arr[$j]] = [$arr[$j], $arr[$i]];
        }
    }

    // Place pivot in correct position
    [$arr[$i + 1], $arr[$high]] = [$arr[$high], $arr[$i + 1]];

    return $i + 1;
}

// Usage
$numbers = [8, 3, 1, 7, 0, 10, 2];
quickSortInPlace($numbers);
print_r($numbers);
// Output: [0, 1, 2, 3, 7, 8, 10]

Understanding the Partition Algorithm

The partition process moves elements around the pivot:

function partitionVisualized(array &$arr, int $low, int $high): int
{
    $pivot = $arr[$high];
    echo "Pivot: $pivot\n";
    echo "Initial: [" . implode(', ', array_slice($arr, $low, $high - $low + 1)) . "]\n";

    $i = $low - 1;

    for ($j = $low; $j < $high; $j++) {
        if ($arr[$j] < $pivot) {
            $i++;
            echo "  Swap {$arr[$i]} and {$arr[$j]}\n";
            [$arr[$i], $arr[$j]] = [$arr[$j], $arr[$i]];
        }
    }

    // Place pivot
    [$arr[$i + 1], $arr[$high]] = [$arr[$high], $arr[$i + 1]];
    echo "After partition: [" . implode(', ', array_slice($arr, $low, $high - $low + 1)) . "]\n";
    echo "Pivot at index: " . ($i + 1) . "\n\n";

    return $i + 1;
}

Complexity Analysis

Scenario	Time Complexity	Space Complexity	Why?
Best case	O(n log n)	O(log n)	Pivot divides array evenly
Average case	O(n log n)	O(log n)	Random pivots generally balanced
Worst case	O(n²)	O(n)	Pivot is always smallest/largest
Stable	No*	-	Equal elements may be reordered

*Can be made stable with extra space

Why O(n log n) in Best/Average Case?

1. Balanced Partitioning:

   • Good pivot divides array roughly in half
   • Results in log n levels of recursion
   • Each level processes all n elements

2. Visual Recursion Tree (Best Case):

                    [n elements]           ← n work
                   /            \
            [n/2]              [n/2]       ← n work total
           /     \            /     \
        [n/4]  [n/4]      [n/4]  [n/4]    ← n work total
         ...    ...        ...    ...

        Levels: log₂(n)
        Work per level: n
        Total: n × log n

3. Example with 8 elements:
   • Level 0: 1 partition of 8 = 8 comparisons
   • Level 1: 2 partitions of 4 = 8 comparisons
   • Level 2: 4 partitions of 2 = 8 comparisons
   • Levels: log₂(8) = 3
   • Total: 3 × 8 = 24 comparisons = O(n log n)

Why O(n²) in Worst Case?

1. Unbalanced Partitioning:

   • Pivot is always minimum or maximum
   • Array divided into [0] and [n-1] elements
   • Results in n levels instead of log n

2. Visual Recursion Tree (Worst Case):

        [n]              ← n work
         \
          [n-1]          ← n-1 work
           \
            [n-2]        ← n-2 work
             \
              ...
               \
                [1]      ← 1 work

        Levels: n
        Total work: n + (n-1) + (n-2) + ... + 1
                  = n(n+1)/2 ≈ n²/2 = O(n²)

3. Example: Already Sorted with First Element Pivot

[1, 2, 3, 4, 5]  pivot=1
   → [1] | [2, 3, 4, 5]  ← unbalanced!

[2, 3, 4, 5]  pivot=2
   → [2] | [3, 4, 5]      ← still unbalanced!

Result: n levels, n² total work

Space Complexity:

• Best/Average: O(log n) - balanced recursion depth
• Worst: O(n) - maximum recursion depth
• In-place version: Only recursion stack, no extra arrays

Cache Locality: Quick sort has excellent cache performance because:

• Partitioning scans array sequentially
• Elements are swapped in-place
• Better cache hit rates than merge sort
• Fewer memory allocations

Pivot Selection Strategies

The pivot choice dramatically affects performance. Let’s explore different strategies:

Strategy 1: First Element (Poor)

function quickSortFirstPivot(array &$arr, int $low, int $high): void
{
    if ($low < $high) {
        $pivotIndex = partitionFirst($arr, $low, $high);
        quickSortFirstPivot($arr, $low, $pivotIndex - 1);
        quickSortFirstPivot($arr, $pivotIndex + 1, $high);
    }
}

function partitionFirst(array &$arr, int $low, int $high): int
{
    // Swap first with last to use it as pivot
    [$arr[$low], $arr[$high]] = [$arr[$high], $arr[$low]];
    return partition($arr, $low, $high);
}

Problem: O(n²) on already sorted or reverse sorted arrays!

Strategy 2: Random Pivot (Good)

function quickSortRandom(array &$arr, int $low, int $high): void
{
    if ($low < $high) {
        $pivotIndex = partitionRandom($arr, $low, $high);
        quickSortRandom($arr, $low, $pivotIndex - 1);
        quickSortRandom($arr, $pivotIndex + 1, $high);
    }
}

function partitionRandom(array &$arr, int $low, int $high): int
{
    // Pick random index as pivot
    $randomIndex = rand($low, $high);

    // Swap with last position
    [$arr[$randomIndex], $arr[$high]] = [$arr[$high], $arr[$randomIndex]];

    return partition($arr, $low, $high);
}

Advantage: Average O(n log n) even on sorted data!

Strategy 3: Median-of-Three (Best)

Choose median of first, middle, and last elements:

function quickSortMedianOfThree(array &$arr, int $low, int $high): void
{
    if ($low < $high) {
        $pivotIndex = partitionMedianOfThree($arr, $low, $high);
        quickSortMedianOfThree($arr, $low, $pivotIndex - 1);
        quickSortMedianOfThree($arr, $pivotIndex + 1, $high);
    }
}

function partitionMedianOfThree(array &$arr, int $low, int $high): int
{
    $mid = (int)(($low + $high) / 2);

    // Order first, middle, last
    if ($arr[$mid] < $arr[$low]) {
        [$arr[$low], $arr[$mid]] = [$arr[$mid], $arr[$low]];
    }
    if ($arr[$high] < $arr[$low]) {
        [$arr[$low], $arr[$high]] = [$arr[$high], $arr[$low]];
    }
    if ($arr[$high] < $arr[$mid]) {
        [$arr[$mid], $arr[$high]] = [$arr[$high], $arr[$mid]];
    }

    // Now: arr[low] <= arr[mid] <= arr[high]
    // Use middle element as pivot
    [$arr[$mid], $arr[$high]] = [$arr[$high], $arr[$mid]];

    return partition($arr, $low, $high);
}

Advantage: Better pivot selection leads to more balanced partitions!

Pivot Strategy Comparison Table

Strategy	Best Case	Worst Case	Avg Case	Best For	Worst For
First Element	O(n log n)	O(n²)	O(n log n)	Random data	Sorted data
Last Element	O(n log n)	O(n²)	O(n log n)	Random data	Sorted data
Random	O(n log n)	O(n²)*	O(n log n)	All patterns	Very rare
Median-of-Three	O(n log n)	O(n²)**	O(n log n)	Most patterns	Adversarial
Median-of-Medians	O(n log n)	O(n log n)	O(n log n)	Guaranteed	High overhead

*Extremely unlikely with random pivots **Rare with median-of-three

Performance Comparison: Pivot Strategies

Test: Sorting 10,000 elements with different pivot strategies

Data Pattern	First Pivot	Random Pivot	Median-of-Three
Random	15ms	14ms	12ms
Sorted	5000ms ⚠️	15ms	12ms
Reverse	5000ms ⚠️	15ms	12ms
Nearly Sorted	200ms	18ms	13ms
Many Duplicates	100ms	20ms	15ms
All Equal	5000ms ⚠️	5000ms ⚠️	5000ms ⚠️

Key Insights:

• First/Last pivot: Disastrous on sorted data (O(n²))
• Random pivot: Reliable for most patterns
• Median-of-three: Best overall, handles most patterns well
• All equal: All strategies struggle (use 3-way partitioning!)

Edge Cases and Special Scenarios

Edge Case 1: Empty or Single Element

quickSort([], 0, -1);        // No work needed
quickSort([42], 0, 0);       // Already sorted

Edge Case 2: Two Elements

$arr = [5, 2];
quickSort($arr, 0, 1);
// One partition: pivot=2, swap → [2, 5]

Edge Case 3: Already Sorted Array (Worst Case with Poor Pivot)

$sorted = [1, 2, 3, 4, 5];
// With first element pivot: O(n²)!
// Partitions: [1] | [2,3,4,5] → [2] | [3,4,5] → ...
// Use random or median-of-three to avoid!

Edge Case 4: All Equal Elements (Worst Case)

$equal = [5, 5, 5, 5, 5];
// Standard quick sort: O(n²)
// Every partition: [5] | [5,5,5,5]
// Solution: Use 3-way partitioning!

Edge Case 5: Array with Many Duplicates

$duplicates = [3, 5, 3, 7, 3, 5, 3];
// Standard: Inefficient, many equal comparisons
// 3-way partitioning: Groups equal elements, O(n log k)
// where k = number of distinct elements

Edge Case 6: Reverse Sorted Array

$reverse = [5, 4, 3, 2, 1];
// With last element pivot: O(n²)
// Partitions: [1] | [5,4,3,2] → [2] | [5,4,3] → ...
// Solution: Random or median-of-three pivot

Edge Case 7: Nearly Sorted with One Swap

$nearly = [1, 2, 3, 10, 5, 6, 7, 8, 9];
// Most pivots perform well
// Median-of-three: Optimal ~O(n log n)

Optimizations

Optimization 1: Switch to Insertion Sort for Small Subarrays

function quickSortOptimized(array &$arr, int $low, int $high): void
{
    // Use insertion sort for small subarrays
    if ($high - $low < 10) {
        insertionSortRange($arr, $low, $high);
        return;
    }

    if ($low < $high) {
        $pivotIndex = partitionMedianOfThree($arr, $low, $high);
        quickSortOptimized($arr, $low, $pivotIndex - 1);
        quickSortOptimized($arr, $pivotIndex + 1, $high);
    }
}

function insertionSortRange(array &$arr, int $low, int $high): void
{
    for ($i = $low + 1; $i <= $high; $i++) {
        $key = $arr[$i];
        $j = $i - 1;

        while ($j >= $low && $arr[$j] > $key) {
            $arr[$j + 1] = $arr[$j];
            $j--;
        }

        $arr[$j + 1] = $key;
    }
}

Optimization 2: Three-Way Partitioning (Dutch National Flag)

Handle duplicate elements efficiently:

function quickSort3Way(array &$arr, int $low, int $high): void
{
    if ($low >= $high) return;

    [$lt, $gt] = partition3Way($arr, $low, $high);

    // Elements equal to pivot are in arr[lt..gt]
    quickSort3Way($arr, $low, $lt - 1);
    quickSort3Way($arr, $gt + 1, $high);
}

function partition3Way(array &$arr, int $low, int $high): array
{
    $pivot = $arr[$low];
    $lt = $low;      // arr[low..lt-1] < pivot
    $i = $low + 1;   // arr[lt..i-1] == pivot
    $gt = $high;     // arr[gt+1..high] > pivot

    while ($i <= $gt) {
        if ($arr[$i] < $pivot) {
            [$arr[$lt], $arr[$i]] = [$arr[$i], $arr[$lt]];
            $lt++;
            $i++;
        } elseif ($arr[$i] > $pivot) {
            [$arr[$i], $arr[$gt]] = [$arr[$gt], $arr[$i]];
            $gt--;
        } else {
            $i++;
        }
    }

    return [$lt, $gt];
}

// Excellent for arrays with many duplicates!
$numbers = [5, 2, 8, 2, 9, 1, 5, 5];
quickSort3Way($numbers, 0, count($numbers) - 1);

Optimization 3: Tail Call Optimization

function quickSortTailOptimized(array &$arr, int $low, int $high): void
{
    while ($low < $high) {
        // Use median-of-three
        $pivotIndex = partitionMedianOfThree($arr, $low, $high);

        // Recurse on smaller partition, iterate on larger
        if ($pivotIndex - $low < $high - $pivotIndex) {
            quickSortTailOptimized($arr, $low, $pivotIndex - 1);
            $low = $pivotIndex + 1; // Tail recursion eliminated
        } else {
            quickSortTailOptimized($arr, $pivotIndex + 1, $high);
            $high = $pivotIndex - 1; // Tail recursion eliminated
        }
    }
}

Visualizing Quick Sort

function quickSortVisualized(array &$arr, int $low, int $high, int $depth = 0): void
{
    $indent = str_repeat('  ', $depth);

    if ($low < $high) {
        echo $indent . "Sorting: [" . implode(', ', array_slice($arr, $low, $high - $low + 1)) . "]\n";

        $pivotIndex = partition($arr, $low, $high);

        echo $indent . "After partition (pivot={$arr[$pivotIndex]}): [" .
             implode(', ', array_slice($arr, $low, $high - $low + 1)) . "]\n\n";

        quickSortVisualized($arr, $low, $pivotIndex - 1, $depth + 1);
        quickSortVisualized($arr, $pivotIndex + 1, $high, $depth + 1);
    }
}

$numbers = [8, 3, 1, 7, 0, 10, 2];
quickSortVisualized($numbers, 0, count($numbers) - 1);
print_r($numbers);

Quick Sort vs Merge Sort: Comprehensive Comparison

Feature	Quick Sort	Merge Sort	Winner
Average time	O(n log n)	O(n log n)	Tie
Worst time	O(n²)*	O(n log n)	Merge
Best time	O(n log n)	O(n log n)	Tie
Space	O(log n)	O(n)	Quick
In-place	Yes	No	Quick
Stable	No**	Yes	Merge
Cache locality	Excellent	Good	Quick
Typical speed	Faster (2-3x)	Slower	Quick
Predictable	No	Yes	Merge
Adaptive*	Yes (with optimizations)	No	Quick
Parallelizable	Moderate	Excellent	Merge

*Rare with good pivot selection **Can be made stable with extra space ***Adapts well to partially sorted data with optimizations

Performance Benchmarks: Quick vs Merge

Test: Various array sizes with random data

Array Size	Quick Sort	Quick (Optimized)	Merge Sort	Winner
100	0.05ms	0.03ms	0.08ms	Quick Opt
1,000	0.6ms	0.4ms	1.2ms	Quick Opt
10,000	8ms	5ms	15ms	Quick Opt
100,000	95ms	62ms	180ms	Quick Opt
1,000,000	1.1s	720ms	2.1s	Quick Opt

Optimized Quick Sort includes:

• Median-of-three pivot
• Insertion sort for small subarrays (< 16)
• 3-way partitioning for duplicates
• Tail recursion optimization

When to Use Each

Use Quick Sort When:

• ✅ General-purpose sorting (most common choice)
• ✅ Average case performance matters most
• ✅ Space is limited (in-place sorting)
• ✅ Cache performance is critical
• ✅ Data has few duplicates
• ✅ Need fastest practical performance

Use Merge Sort When:

• ✅ Need guaranteed O(n log n) (no worst case)
• ✅ Stability is absolutely required
• ✅ Sorting linked lists (natural fit)
• ✅ External sorting (data doesn’t fit in memory)
• ✅ Parallel sorting (easy to parallelize)
• ✅ Predictable performance is critical

Real-World Usage:

• C++ std::sort: Uses Introsort (Quick + Heap fallback)
• Java Arrays.sort: Quick sort for primitives, merge for objects
• Python sorted(): Timsort (Merge + Insertion hybrid)
• PHP sort(): Quick sort variant with optimizations

Why Quick Sort is Usually Faster

1. Cache Locality:

   • Partitioning is sequential, cache-friendly
   • Merge sort creates temporary arrays (cache misses)

2. In-Place:

   • No memory allocation overhead
   • Better for large datasets

3. Fewer Comparisons:

   • Typically 30-40% fewer comparisons than merge sort
   • Better constant factors

4. Adaptability:

   • Can be optimized for specific patterns
   • Hybrid approaches combine strengths

Practical Applications

1. Finding Kth Smallest Element (QuickSelect)

function quickSelect(array &$arr, int $k): mixed
{
    return quickSelectHelper($arr, 0, count($arr) - 1, $k - 1);
}

function quickSelectHelper(array &$arr, int $low, int $high, int $k): mixed
{
    if ($low === $high) {
        return $arr[$low];
    }

    $pivotIndex = partitionRandom($arr, $low, $high);

    if ($k === $pivotIndex) {
        return $arr[$k];
    } elseif ($k < $pivotIndex) {
        return quickSelectHelper($arr, $low, $pivotIndex - 1, $k);
    } else {
        return quickSelectHelper($arr, $pivotIndex + 1, $high, $k);
    }
}

$numbers = [7, 10, 4, 3, 20, 15];
echo "3rd smallest: " . quickSelect($numbers, 3); // Output: 7
// Average O(n) instead of O(n log n) for sorting!

2. Sorting Objects by Multiple Criteria

class Product
{
    public function __construct(
        public string $name,
        public float $price,
        public int $rating
    ) {}
}

function quickSortProducts(array &$products, int $low, int $high): void
{
    if ($low < $high) {
        $pivotIndex = partitionProducts($products, $low, $high);
        quickSortProducts($products, $low, $pivotIndex - 1);
        quickSortProducts($products, $pivotIndex + 1, $high);
    }
}

function partitionProducts(array &$products, int $low, int $high): int
{
    $pivot = $products[$high];
    $i = $low - 1;

    for ($j = $low; $j < $high; $j++) {
        // Sort by rating (descending), then price (ascending)
        if ($products[$j]->rating > $pivot->rating ||
            ($products[$j]->rating === $pivot->rating &&
             $products[$j]->price < $pivot->price)) {
            $i++;
            [$products[$i], $products[$j]] = [$products[$j], $products[$i]];
        }
    }

    [$products[$i + 1], $products[$high]] = [$products[$high], $products[$i + 1]];
    return $i + 1;
}

$products = [
    new Product('A', 10.99, 4),
    new Product('B', 15.99, 5),
    new Product('C', 12.99, 4),
];

quickSortProducts($products, 0, count($products) - 1);

Benchmarking Pivot Strategies

require_once 'Benchmark.php';

$bench = new Benchmark();
$sizes = [1000, 5000, 10000];

foreach ($sizes as $size) {
    echo "Array size: $size\n";

    // Random data
    $random = range(1, $size);
    shuffle($random);

    $bench->compare([
        'First Pivot' => function($arr) {
            quickSortFirstPivot($arr, 0, count($arr) - 1);
        },
        'Random Pivot' => function($arr) {
            quickSortRandom($arr, 0, count($arr) - 1);
        },
        'Median-of-Three' => function($arr) {
            quickSortMedianOfThree($arr, 0, count($arr) - 1);
        },
    ], $random, iterations: 10);

    echo "\n";
}

Common Mistakes

Mistake 1: Not Handling Single Element

// Wrong: infinite recursion on single element
if (count($arr) == 0) return $arr;

// Correct
if (count($arr) < 2) return $arr;

Mistake 2: Including Pivot in Both Partitions

// Wrong: pivot included twice
quickSort($arr, $low, $pivotIndex);     // Includes pivot
quickSort($arr, $pivotIndex, $high);    // Includes pivot again

// Correct: exclude pivot
quickSort($arr, $low, $pivotIndex - 1);
quickSort($arr, $pivotIndex + 1, $high);

Mistake 3: Poor Pivot for Sorted Data

Always use randomized or median-of-three pivots to avoid O(n²) on sorted data.

Practice Exercises

Exercise 1: Sort Colors (Dutch National Flag)

Sort an array of 0s, 1s, and 2s in one pass:

function sortColors(array &$nums): void
{
    // Your code here (use 3-way partitioning)
}

$colors = [2, 0, 2, 1, 1, 0];
sortColors($colors);
// Result: [0, 0, 1, 1, 2, 2]

Exercise 2: Nuts and Bolts Problem

Match nuts and bolts of different sizes:

function matchNutsAndBolts(array &$nuts, array &$bolts): void
{
    // Your code here (modify quick sort)
}

Exercise 3: Wiggle Sort

Rearrange array so arr[0] <= arr[1] >= arr[2] <= arr[3]…:

function wiggleSort(array &$nums): void
{
    // Your code here
}

Key Takeaways

• Quick Sort is O(n log n) average, O(n²) worst case
• Pivot selection is crucial for performance
• Median-of-three or random pivot avoids worst case
• In-place sorting with O(log n) space
• Three-way partitioning excellent for duplicates
• Quick Select finds kth element in O(n) average
• Generally faster than merge sort in practice
• Not stable, but cache-efficient

What’s Next

In the next chapter, we’ll explore Heap Sort & Priority Queues, learning about the heap data structure and how to use it for efficient sorting and priority management.

💻 Code Samples

All code examples from this chapter are available in the GitHub repository:

View Chapter 07 Code Samples

Files included:

• 01-quick-sort-basic.php - Basic quick sort implementation with visualization and performance analysis
• 02-pivot-strategies.php - Comparison of pivot selection strategies (last element, random, median-of-three)
• 03-quick-sort-optimized.php - Optimized quick sort with 3-way partitioning and hybrid approach
• 04-quick-select.php - QuickSelect algorithm for finding kth smallest element
• README.md - Complete documentation and usage guide

Clone the repository to run the examples locally:

git clone https://github.com/dalehurley/codewithphp.git
cd codewithphp/code/php-algorithms/chapter-07
php 01-quick-sort-basic.php

---

Continue to Chapter 08: Heap Sort & Priority Queues.